N种排序算法(持续更新中)

1.选择排序 selection sort

2.插入排序 insertion sort

3.希尔排序 shell sort

4.归并排序 merge sort

5.快速排序 quick sort

6.基数排序 radix sort

 

1.选择排序 selection sort

每次遍历整个数组，选出其中最小值。如果数组长度为n，则需要(n-1)+(n-2)+...+2+1次操作，因此时间复杂度为。

选择排序的代码：

>>> def findSmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

>>> def selectionSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr

2.插入排序 insertion sort

用个例子来说明，arr=[5,1,2,4,7,3]。插入排序的过程如下图所示。

数组中的第i个元素与第i-1个元素比较，arr[i]<arr[i-1]，则交换arr[i]和arr[i-1]，并继续与arr[i-2]比较，直到大于前一个元素。

和选择排序不同的是，插入排序所需的时间取决于输入中元素的初始顺序。对于随机排列的长度为N且主键不重复的数组，平均情况下插入排序需要~N^2/4次比较以及~N^2/4次交换。最坏情况下需要~N^2/2次比较和~N^2/2次交换，最好情况下需要N-1次比较和0次交换。

插入排序的代码：

def insertSort(arr):
    for i in range(1,len(arr)):
        for j in range(i,0,-1):
            if arr[j]<arr[j-1]:
                temp=arr[j]
                arr[j]=arr[j-1]
                arr[j-1]=temp
    return arr

通过在内循环中将较大的元素向右移动而不是交换，便可以大幅度提高插入排序的速度。同样以arr=[5,1,2,4,7,3]为例。如下图所示，令对比的基准base=arr[1]，如果base<arr[0]，则arr[0]向右移动一位，即arr[1]=arr[0]，内循环结束，即arr[0]=base，新数组为arr=[1,5,2,4,7,3]。令base=arr[2]，如果base<arr[1]，则arr[1]向右移动一位，arr[2]=arr[1]，继续内循环，即对比base和arr[0]，在本例中base>arr[0]，结束内循环，并且arr[1]=base。新数组为arr=[1,2,5,4,7,3]。

快速插入排序的代码：

def insertSort2(arr):
    for i in range(1,len(arr)):
        _base=arr[i]
        k=0
        for j in range(i,0,-1):
            if _base<arr[j-1]:
                arr[j]=arr[j-1]
            else:
                k=j
                break
        arr[k]=_base
        
    return arr

3.希尔排序 shell sort

对于大规模乱序数组而言，插入排序很慢，因为它只交换相邻的元素，因此元素只能一点一点地从数组的一段移动到另一端。希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。即希尔排序使数组中任意间隔为h的元素都是有序的。例如

[2, 6, 3, 5, 10, 4, 8, 21, 1, 34, 7, 9]

当h=4时，使得2-10-1有序，6-4-34有序，3-8-7有序，5-21-9有序，得到的新数组为

[1, 4, 3, 5, 2, 6, 7, 9, 10, 34, 8, 21]

然后h=1时，就是普通的插入排序，得到的新数组为

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 21, 34]

对于本例，使用希尔排序一共交换13次，而使用插入排序的交换次数为21次

希尔排序的代码：

def ShellSort(arr):
    h=1
    while h<len(arr)/3:
        h=3*h+1
    
    while h>=1:
        for i in range(h,len(arr)):
            for j in range(i,h-1,-h):
                if arr[j]<arr[j-h]:
                    temp=arr[j]
                    arr[j]=arr[j-h]
                    arr[j-h]=temp
                else:
                    break
        h=math.floor(h/3)
    return arr

4.归并排序 merge sort

基于分而治之的思想(divide and conquer, D&C)，要将一个数组排序，可以先（递归地）将它分成两半分别排序，然后将结果归并起来。归并的一种直截了当的做法是将两个不同的有序数组归并到第三个数组中。例如如下数组：

[2,4,9,13,1,5,8,23]

是由两个有序数组sub1=[2,4,9,13]和sub2=[1,5,8,23]组成的，将这两个有序的子数组归并为一个数组，就可以先创建一个长度为8的辅助数组aux，然后sub1[0]和sub2[0]作比较，把小的那个写入到aux[0]中，在本例中，sub2[0]<sub1[0]，因此aux[0]=sub2[0]，然后再取sub2[1]与sub1[0]对比，如此循环，终止条件为sub1或者sub2取到了最后一个数。

归并方法的代码：

def merge(arr,low,mid,high):
    aux=[0]*len(arr)
    i=low
    j=mid+1

    for k in range(low,high+1):
        if i>mid:
            aux[k]=arr[j]
            j=j+1
        elif j>high:
            aux[k]=arr[i]
            i=i+1
        elif arr[i]<arr[j]:
            aux[k]=arr[i]
            i=i+1
        else:
            aux[k]=arr[j]
            j=j+1
    return aux

递归实现：

def merge(low,mid,high):
    i=low
    j=mid+1

    for k in range(low,high+1):
        aux[k]=arr[k]

    for k in range(low,high+1):
        if i>mid:
            arr[k]=aux[j]
            j=j+1
        elif j>high:
            arr[k]=aux[i]
            i=i+1
        elif aux[i]<aux[j]:
            arr[k]=aux[i]
            i=i+1
        else:
            arr[k]=aux[j]
            j=j+1

def recurisonSort(low,high):
    if low<high:
        mid=math.floor(low+(high-low)/2)
        recurisonSort(low,mid)
        recurisonSort(mid+1,high)
        merge(low,mid,high)

def mergeSort(_arr):
    global aux
    aux=[0]*len(_arr)

    global arr
    arr=[]
    for i in _arr:
        arr.append(i)
    
    recurisonSort(0,len(arr)-1)
    return arr

对于长度为N的任意数组，递归归并排序需要1/2NlgN-NlgN次比较，最多需要访问数组6NlgN次。

直接进行的是两两归并，然后是四四归并，进而八八归并，一直下去。这种实现方法比标准递归方法所需要的代码量更少。非递归实现：

def mergeSort2(_arr):
    length=len(_arr)
    global aux
    aux=[0]*length

    global arr
    arr=[]
    for j in _arr:
        arr.append(j)

    i=1
    while(i<length):
        for k in range(0,length-i,2*i):
            high=min(k+2*i-1,length-1)
            if k<high:
                merge(k,k+i-1,high)
        i=i*2
        
    print(arr)

5.快速排序 quick sort

同样基于分而治之的思想：1.找出简单的基线条件；2.确定如何缩小问题的规模，使其符合基线条件。

那么将D&C思想应用于排序任务中，其思路应如下：

基线条件就是只有一个元素的数组，这样的数组顺序就是自己。在数组中任取一个元素作为基准值，那么该数组将会被划分为三部分

　　小于基准值的子数组 + 基准值 + 大于基准值的子数组

这样就会不断地缩小数组的规模，直到只剩一个元素为止。

快速排序的代码：

>>> def quicksort(arr):
    if len(arr) < 2:
        return arr
    else:
        pivot = arr[0]
        less = [i for i in arr[1:] if i <= pivot]
        greater = [i for i in arr[1:] if i > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)

    
>>> arr = [3,5,1,9,7]
>>> quicksort(arr)
[1, 3, 5, 7, 9]
>>> 

其实，排序的方法已经包含在各种语言中了，比如Python和C#都是使用Sort方法，就可以对一个数组进行从小到大的排序了。不过了解算法的本质应该也不是什么坏事吧。

6.基数排序 radix sort

准备标号为0-9的10个格子，对于一个给定的数组，先按照个位上的数，把这组数据放到相应标号的格子中。依次弹出格子中的数，构成新数组，然后再按照十位上的数，把数据再次放到对应标号的格子中，如果没有十位，则按0处理，循环进行，直到排到最高位。例如：[102,473,251,14,863]，基数排序过程如下方动图所示。

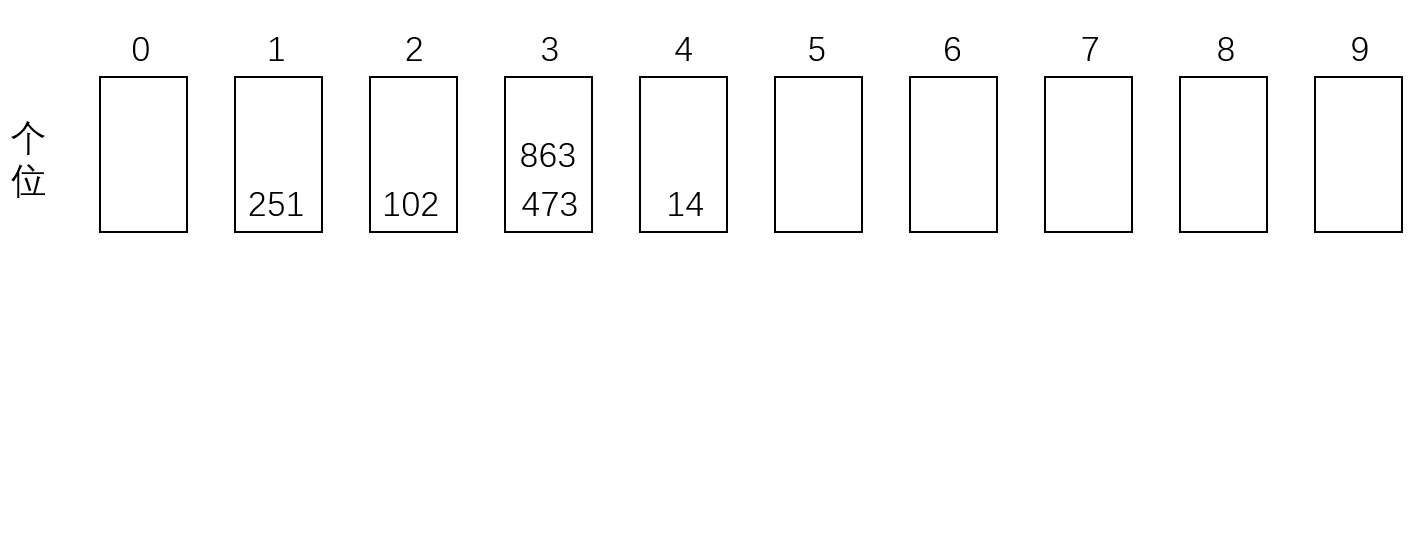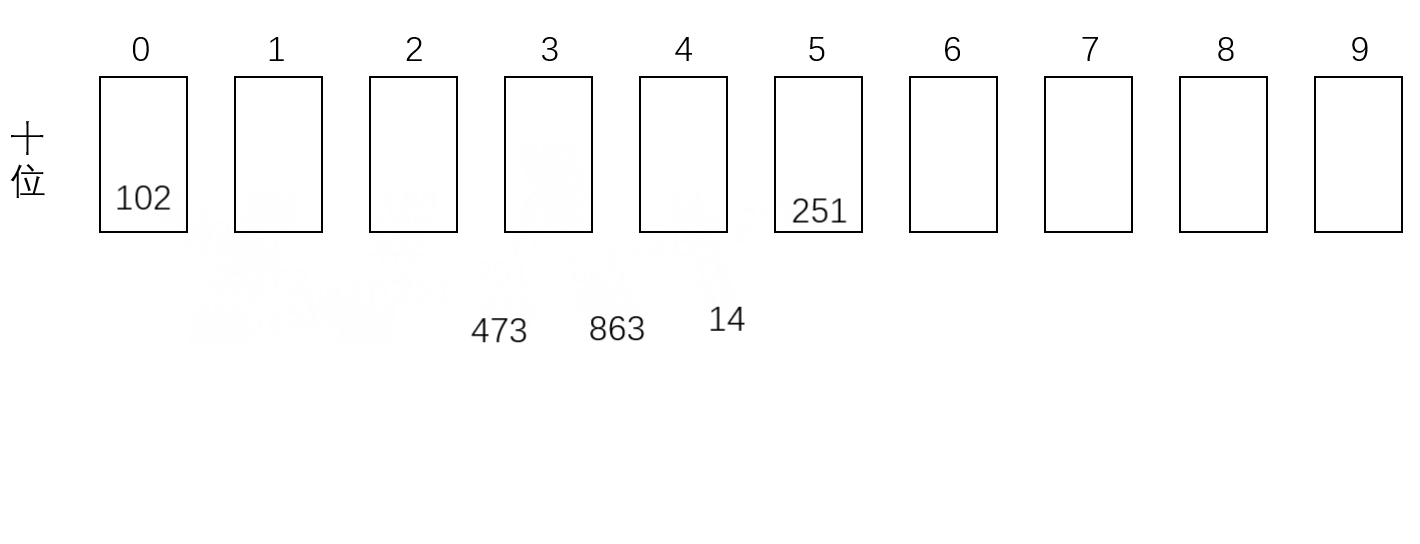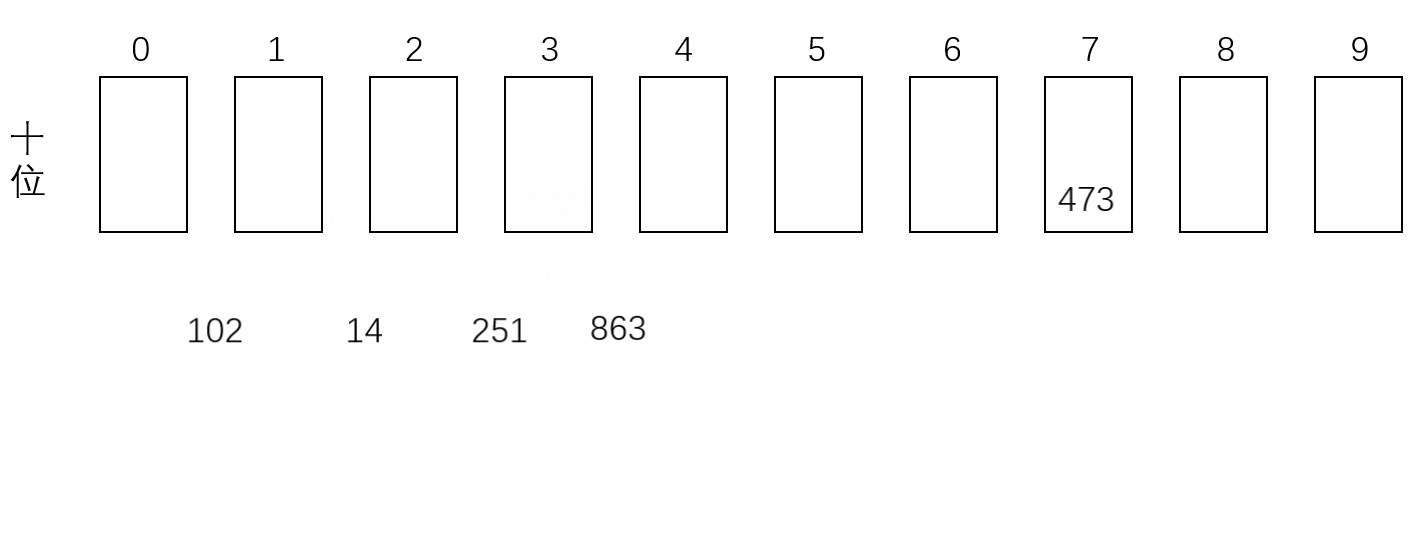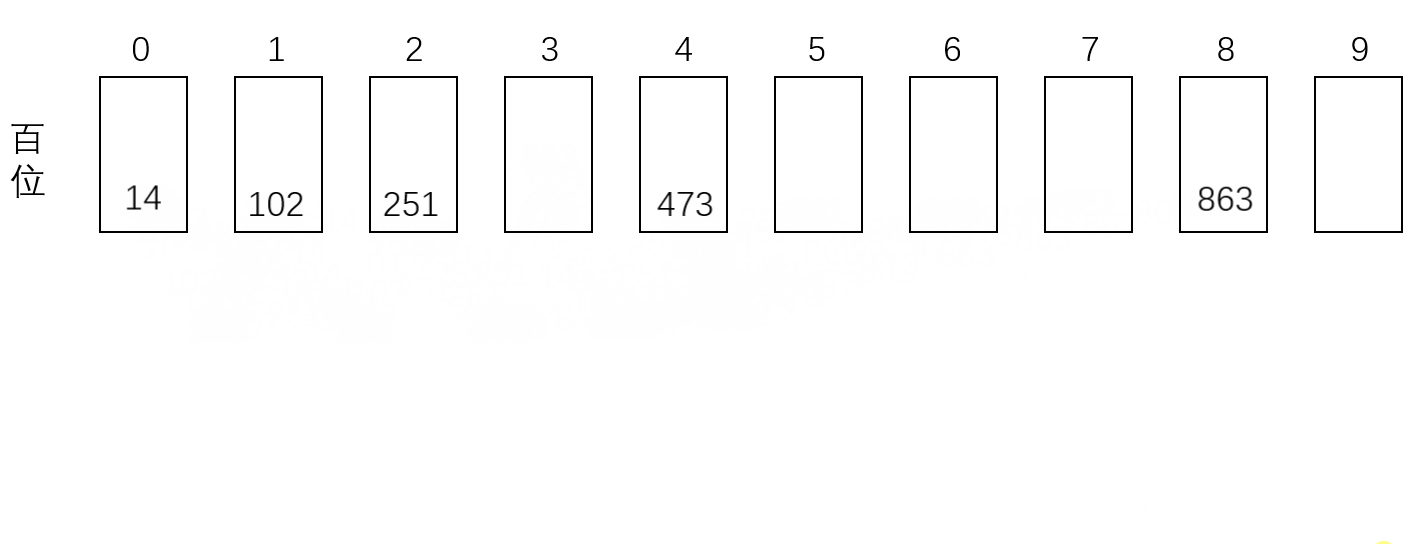
可见，基数排序的时间复杂度是O(m*n)，其中m是位数最高的元素的长度, n是数组长度。代码如下：

def radixSort(nums):
    bags=[[] for i in range(10)]
    terms=[]
    m=0
    for i in nums:
        term=str(i)
        terms.append(term)
        m=max(m,len(term))
    
    for i in range(-1,-m-1,-1):
        for k in terms:
            if len(k)<-i:
                bags[0].append(k)
            else:
                val=int(k[i])
                bags[val].append(k)
        _terms=[]
        for bag in bags:
            _terms.extend(bag)
        terms=_terms
        bags=[[] for i in range(10)]
    return [int(i) for i in terms]

refs:

《算法》（第四版）

《算法图解》

https://blog.csdn.net/Zhouzi_heng/article/details/109017751