机器学习ROC图解读

1. 分类器评估指标

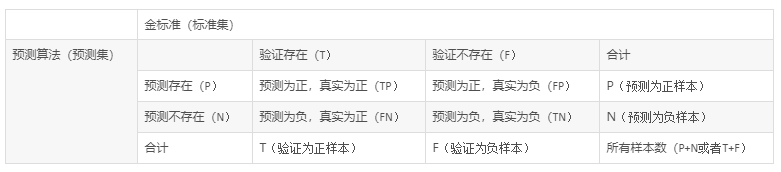
对于二分类问题，可将样例根据其真实类别和分类器预测类别划分为：
真正例（True Positive，TP）：真实类别为正例，预测类别为正例。
假正例（False Positive，FP）：真实类别为负例，预测类别为正例。
假负例（False Negative，FN）：真实类别为正例，预测类别为负例。
真负例（True Negative，TN）：真实类别为负例，预测类别为负例。

2. 精确度，召回率，真阳性，假阳性

精确度( precision )：TP / ( TP+FP ) = TP / P  

召回率（recall）：TP / (TP + FN ) = TP / T

真阳性率（True positive rate）：TPR = TP / ( TP+FN ) = TP / T  （敏感性 sensitivity）

假阳性率（False positive rate）：FPR = FP / ( FP + TN ) = FP / F  （特异性：specificity）

准确率（Accuracy）：Acc = ( TP + TN ) / ( P +N )

F-measure：2*recall*precision / ( recall + precision )

ROC曲线：FPR为横坐标，TPR为纵坐标

PR曲线：recall为横坐标，precision 为纵坐标

 

3. ROC图

 

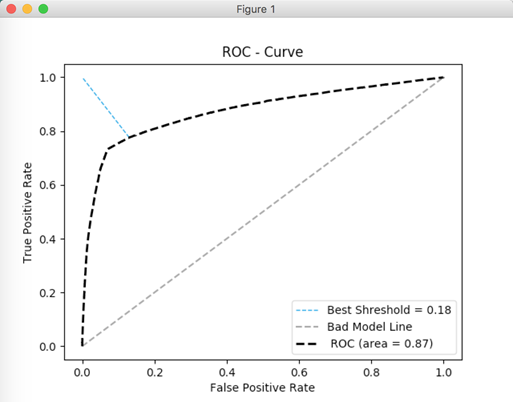
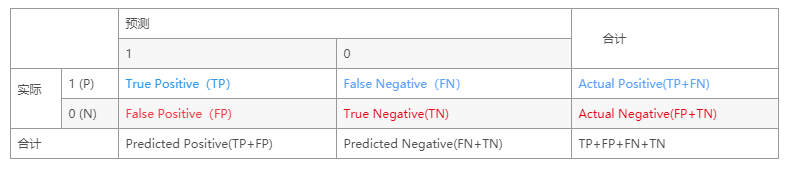
• 纵坐标是true positive rate(TPR)  = TP / (TP+FN=P) （分母是横行的合计）直观解释：实际是1中，猜对多少
• 横坐标是false positive rate(FPR) = FP / (FP+TN=N)  直观解释：实际是0中，错猜多少

4. AUC

AUC（Area Under Curve），就是这条ROC曲线下方的面积了。越接近1表示分类器越好。 但是，直接计算AUC很麻烦，但由于其跟Wilcoxon-Mann-Witney Test等价，所以可以用这个测试的方法来计算AUC。Wilcoxon-Mann-Witney Test指的是，任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score（score指分类器的打分）。

随着FPR的上升，ROC曲线从原点(0, 0)出发，最终都会落到(1, 1)点。ROC便是其右下方的曲线面积。下图展现了三种AUC的值：

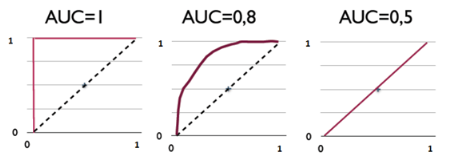
AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。

0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在AUC < 0.5的情况

AUC对于每一个做机器学习的人来说一定不陌生，它是衡量二分类模型优劣的一种评价指标，表示正例排在负例前面的概率。其他评价指标有精确度、准确率、召回率，而AUC比这三者更为常用。因为一般在分类模型中，预测结果都是以概率的形式表现，如果要计算准确率，通常都会手动设置一个阈值来将对应的概率转化成类别，这个阈值也就很大程度上影响了模型准确率的计算。

 我们不妨举一个极端的例子：一个二类分类问题一共10个样本，其中9个样本为正例，1个样本为负例，在全部判正的情况下准确率将高达90%，而这并不是我们希望的结果，尤其是在这个负例样本得分还是最高的情况下，模型的性能本应极差，从准确率上看却适得其反。而AUC能很好描述模型整体性能的高低。这种情况下，模型的AUC值将等于0（当然，通过取反可以解决小于50%的情况，不过这是另一回事了）。