这个算法有如下几个数据结构
1 lft 代表左 left
2 rgt 代表右 right
3 lvl 代表所在的层次 level
下面这个图是一个典型的结构
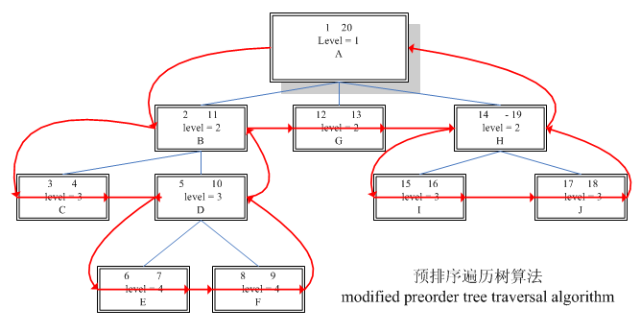
我们先看一些使用方法
1 查看整个树(A)有多少节点(包含自己)
直接看根节点就行了 (right-left+1)/2 = (20-1+1)/2 = 10
这个数有10个节点
2 查看从节点A到E的路径
select * from tree where lft between 1 and 6 and rgt between 7 and 20 order by lft
得到的结果是A,B,D,E 这4个节点的数据,且按照访问路径的顺序
如果2个节点之间不是上下级的关系，则查询没有结果
反向也是一样的，可以拿到底部一个节点，到上级节点的路径
select * from tree where lft between 1 and 6 and rgt between 7 and 20 order by lft desc
唯一的区别就是排序是反向的就行了。
3 得到某个节点下面的所有节点，且按照树状结构返回
我们用B做例子
select * from tree where lft>2 and right<11 order by lft
拿到的结果是 C,D,E,F,而且顺序也是正确的。
4 拿到所有下2级的子节点
我们A做例子，这次加上了lvl的参数,因为A的level是1，所以我们查询level不大于3的。
select * from tree where lft>2 and right<11 and lvl<=3 order by lft
下面看我们新增加一个节点的方法。
我们在根节点的下面，G节点的右侧增加一个X节点
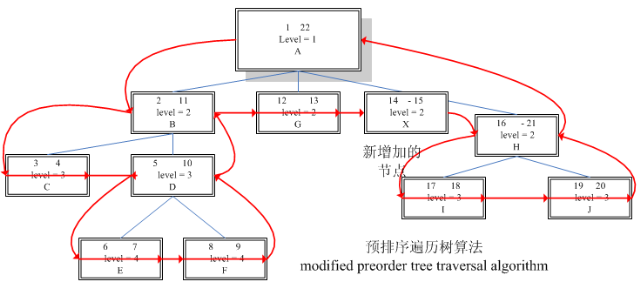
我们要做的工作就是
1 G节点的右参数为13
2 变更所有的受影响的节点,给新节点腾出空位子
所有左节点比G节点大的，都增加2
update tree set lft=lft+2 where lft>12
所有右节点比G节点大的，都增加2
update tree set rgt=rgt+2 where rgt>13
3 新节点放在空位子上,lft=14,rgt=15
这样就完成了一个新节点的增加操作。
1 lft 代表左 left
2 rgt 代表右 right
3 lvl 代表所在的层次 level
下面这个图是一个典型的结构
我们先看一些使用方法
1 查看整个树(A)有多少节点(包含自己)
直接看根节点就行了 (right-left+1)/2 = (20-1+1)/2 = 10
这个数有10个节点
2 查看从节点A到E的路径
select * from tree where lft between 1 and 6 and rgt between 7 and 20 order by lft
得到的结果是A,B,D,E 这4个节点的数据,且按照访问路径的顺序
如果2个节点之间不是上下级的关系，则查询没有结果
反向也是一样的，可以拿到底部一个节点，到上级节点的路径
select * from tree where lft between 1 and 6 and rgt between 7 and 20 order by lft desc
唯一的区别就是排序是反向的就行了。
3 得到某个节点下面的所有节点，且按照树状结构返回
我们用B做例子
select * from tree where lft>2 and right<11 order by lft
拿到的结果是 C,D,E,F,而且顺序也是正确的。
4 拿到所有下2级的子节点
我们A做例子，这次加上了lvl的参数,因为A的level是1，所以我们查询level不大于3的。
select * from tree where lft>2 and right<11 and lvl<=3 order by lft
下面看我们新增加一个节点的方法。
我们在根节点的下面，G节点的右侧增加一个X节点
我们要做的工作就是
1 G节点的右参数为13
2 变更所有的受影响的节点,给新节点腾出空位子
所有左节点比G节点大的，都增加2
update tree set lft=lft+2 where lft>12
所有右节点比G节点大的，都增加2
update tree set rgt=rgt+2 where rgt>13
3 新节点放在空位子上,lft=14,rgt=15
这样就完成了一个新节点的增加操作。
