字符串最小表示法问题,小优化后的双指针线性算法以及一个小性质.

1.原始双指针线性算法

以下约定字符串下标从0开始,字符串长度为n, 问题描述以及双指针线性算法参见最小表示法 - OI Wiki (oi-wiki.org). (如果你看不懂下一段的总结,请仔细阅读oiwiki上的讲解)

总结来说,双指针算法是: 维护两个可能的指针i,j, 找到以它们开头的字符串的第一个不同的位置:S[i+k]和S[j+k],S[i+k]>S[j+k]将导致i~i+k都不可能为最小表示的开头,i~i+k被淘汰(S[i+k]<S[j+k]时类似). 每一轮,比较k+1个字符都能使i或j前进k+1步,i或j达到n算法将结束,该算法最多执行步数不超过3n.(粗略考虑一下前面若干轮比较总共(n-2)+(n-1)次使i=n-2,j=n-1,然后比较n次才决出i和j谁更优,总共3n-3步, 当然不一定存在能跑满3n-3步的例子,这里只是做粗略分析).

 

2.小优化

  下面考虑对这个双指针算法进行优化, 首先为了方便,我们约定i<j(上述算法过程中如果i跳到j后面去了,交换一下i,j即可)

  上述算法(以下称算法1)中的被淘汰的下标不可能为最小表示的开头,我们称这些下标死了(dead), 容易发现,算法过程中始终有{0,...j-1}\i (即0~j-1除去i)都是dead的,因为指针j(i同理)前进k步意味着j~j+k-1都dead了.

我们考虑两种情况:

  1. S[i+k]<S[j+k], 此时同算法1,让j前进k+1步即可

  2. S[i+k]>S[j+k], 算法1中会让i前进k+1步即i+=k+1,再细分三种情况讨论:

    2.1: i+k+1<j, 此时算法1将进入下一轮. 而我们发现,不仅这步得到的i~i+k是dead的,之前我们已经确认{0,...j-1}\i都是dead的了,可知i+k+1~j-1也是dead的,那么我们可以直接让i=j,j++来帮助i向后跳更多.  (再强调一次正确性: 这步得知i~i+k是dead的,之前已知{0,...j-1}\i是dead的,那么结合起来知0~j-1都dead,那么我们显然可以从i=j,j=j+1开始新的一轮比较,继续寻找最小表示)

   2.2: i+k+1>j, 此时算法1在我们的约定i<j下仅仅swap(i,j)就进入下一轮. 而我们发现, 之前已知{0,...j-1}\i是dead,这步得知i~i+k是dead,结合起来会有0~i+k是dead的, 那么我们直接让i+=k+1然后让j=i+1就向后跳了更多.

    2.3: i+k+1=j, 此时同算法1, 让i+=k+1,同时加完后i==j,所以让j++以保证比较的两个字符串开头下标不同.

 

总结来说,会发现,若S[i+k]<S[j+k],同算法1,j直接往后跳, S[i+k]>S[j+k],我们可以将两段dead的拼起来(综合2.1~2.3可知我们发现0~max(j,i+k+1)均dead),从而让i,j都有后移. 渐进复杂度和算法1一样都是O(n)的,只不过经过这些小优化常数更小,实际跑起来更快一丢丢.

参考代码:

int MinPresent(const string& s){
    //s已经"二倍拼接",例如输入字符串为ababc,那么传入函数的字符串为ababcabab, 这样下标不用取模
    //下标从0开始
    int i=0,j=1,n=(1+s.length())/2;    //n为原串长度
    while(j<n){
        int k=0;
        for(;k<n;k++){
            if(s[i+k]==s[j+k]) continue;

            if(s[i+k]<s[j+k]) j=j+k+1;    //情况1
            else{
                i+=k+1;
                if(i>j) j=i+1;    //情况2.2,这种情况对应着[i...j...大...小], i跳到大后面,顺便j也被淘汰了! 
                else i=j,j++;  //情况2.1和2.3
            }
            break;
        }
        if(k==n) break;
    }
    return i;
}

 

3.小优化的算法中的一个小性质

  以下称经过小优化后的算法1为算法2, 算法2有一个性质: 算法过程中S[i~j-1]是Lyndon word.(Lyndon word的一个定义是它字典序小于它的所有真后缀)

  用归纳法可以证明:

    首先对于初始i=0,j=1和上面提到的情况2后导致j=i+1这种j=i+1的情况,S[i~j-1]=S[i,i]是一个字母,显然是Lyndon word.

    其次考虑j>i+1的情况, 这种情况显然是经过上面提到的情况1(即S[i+k]<S[j+k]而j往后跳k+1步)转移来的,

      子情况1: 上一个状态是j=i+1,而经过S[i+k]<S[j+k]转移来,此时有S[i~i+k-1]=S[j~j+k-1]=S[i+1~i+k](这表明S[i~i+k]是同一个字母循环构成的,例如aaaaa)且S[j+k]=S[i+1+k]>S[i+k], 即j往后跳k+1步后,新的S[i~j-1]为S[i~i+k+1]为形如aaaaab的串,这样的串显然为Lyndon word. (这种子情况的例子如:S=aaabc,i=0,j=1,此时k=2)

      子情况2: 上一个状态是j>i+1,而经过S[i+k]<S[j+k]转移来.

        首先有一个引理:对于一个Lyndon word:A=TY(S是A的前缀), 则B=AAA..ATx且保证x>Y[0]时有B也是Lyndon word. 

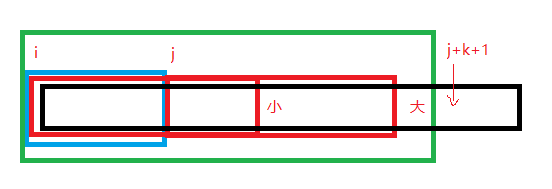
　　 当i+k+1<=j时,新的S[i~j-1]是ATx的形式且x>Y[0],根据引理容易得知其仍为Lyndon word. 如下图所示,原S[i~j-1]为蓝框(根据归纳法假设,它是Lyndon word),新的S[i~j-1]为绿框,红框为两个字符串的相等段.

        

        当i+k+1>j时, 新的S[i~j-1]是A...ATx的形式且x>Y[0],根据引理容易得知其仍为Lyndon word. 如下图所示,原S[i~j-1]为蓝框(根据归纳法假设,它是Lyndon word),新的S[i~j-1]为绿框,红框为两个字符串的相等段,由于S[i~i+k-1]=S[j~j+k-1],即S[i~j+k-1]有一个长度为k的border,那么S[i~j+k-1]以k为周期,所以S[i~j+k-1]为A...AT的形式,而新的S[i~j-1]就为A...ATx的形式了(x>Y[0]).

        

 

     

4.结语

  本文介绍了最小表示法问题的双指针线性算法的一点小优化,是常数上的优化. 然后发现了这个算法过程中的一个小性质:即S[i~j-1]是Lyndon word,这个结论可能不怎么常用,但强调了最小表示法和Lyndon word之间的联系.

   注: 算法1中不具备S[i~j-1]是Lyndon word的性质, 例如S=ababbaa, 算法1第二轮开始会有i=0,j=2然后跳到i=2,j=6,此时S[i~j-1]=S[2~5]=abab不是Lyndon word.