任务安排问题 贪心 朴实思路

【问题描述】有n个任务1~n。假设：

同一个时间单位你只能处理一项任务；

任务i只能在时刻 ri 后开始处理。 （r1,…rn是给定的）

任务i需要 pi个时间单位才能完成。（p1,…,pn是给定的）

一个任务可分成多次处理（可停下来等之后继续处理）。

设计方案使得∑ti最小，ti为任务i被完成的时刻。

例:

 

 

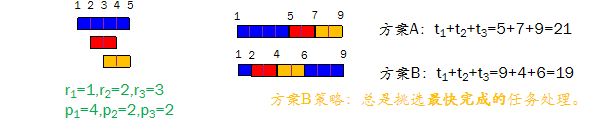
吐槽:这个题的要求:"使得∑ti最小"太奇怪了,不懂有什么实际意义,比如说所有任务完成时刻最小还有实际意义,这个要求可能只是为了作为"贪心"的练习题吧

朴素解法:

用一个数组(队列)存下目前能开始的任务，然后挑需要时长最短的来做一下
记录新任务入队时间点,在时间推进过程中判断有无新任务入队

定义'重要时间点':有任务结束或新任务入队
每两个重要时间点之间都 遍历队列找时长最短的(可堆优化)

例如上图方案B:

时刻1~时刻2之间挑任务1(队列中仅有一个任务)

时刻2~时刻3之间挑任务2

时刻3(新任务入队)~时刻4(一个任务完成)挑任务2

时刻4~时刻6挑任务3

时刻6~时刻9挑任务1

 

最后:本题没有找到oj就不附上代码了,有找到oj的朋友还望告知给博主QAQ