机器学习2--逻辑回归

　　线性模型的核心是一个线性函数 s= w^Tx，即将所有输入变量进行线性组合， 对于线性回归问题（linear regression），输入x，输出w^Tx；对于线性分类(linear classification)问题，需要离散的输出值，例如输出1表示某个样本属于类别C1，输出0表示不属于类别C1, 这时候只需要简单的在线性函数的基础上附加一个阈值即可，通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属; 对于第三种问题逻辑回归，输出值是一个介于0和1之间的概率值。

问题       

我们用一个例子来讲解什么是逻辑回归模型：假设我们想要根据一个人的心跳频率，胆固醇水平，年龄体重等等因素推测他患心脏病的概率，很明显我们不能百分百断定他是否患有心脏病，但我们可以根据这些已知的条件来推测他患心脏病的概率。这就用到了逻辑回归模型，得出的结果要比普通二分类模型更为精确，结果越接近1说并他患心脏病的概率就越大。

模型

　　　　　　　　　　　　　　　　　　　　　　　　　　　　h(x) = θ(w^Tx)

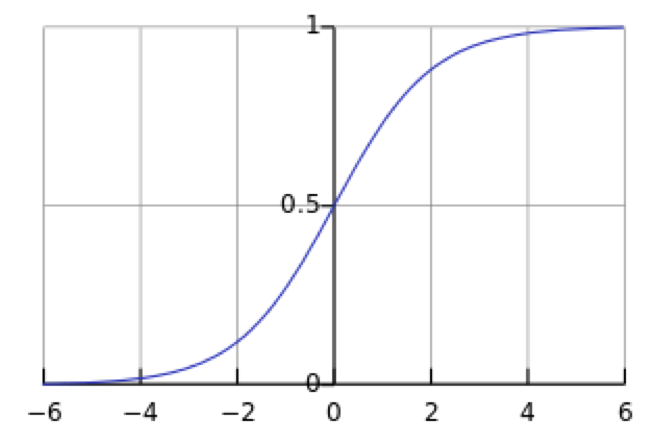
其中θ为logistic函数或者sigmoid函数，其函数形式为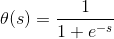, 对应的函数图像是一个取值在0和1之间的S型曲线：

　　　　　　　　　　　　　　　

决策函数

回到我们在文章开头提出的的问题，对于给定的输入x（即待预测者的各项指标）预测他患心脏病的概率，我们可以得到一个目标函数或预测函数:

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

h(x)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1(患心脏病)和类别-1(不换心脏病)的概率分别为:

　　　　　　　　　　　　　　　　　　　　　　　　　

我们用θ(w^Tx)代替h(x), 且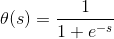, , 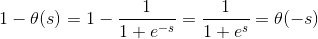因此我们可以得到 P(y|x) = θ(y w^Tx))

损失函数

在逻辑回归模型中我们采用对数损失函数并用极大似然估计求解参数，下面我将从数学角度解释如何为什么会采用对数的损失函数：

因为我们数据集中的数据点（x₁，y₁）,...,（x_N，y_N）之间是相互独立的，所以对于整个数据集而言，求得所有y_n 的概率是

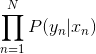　　　　　　　　　　　　　　　　　　　　　　　　　　　　                                                                                         (1)

使用极大似然估计法计可以算出使得上述概率值最大的参数w，为方便计算，我们将其等价转化为求解下边式子的最小值：

　　　　　　　　　　　　　　　　　　　　　　　                                    (2)

因为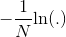是单调递减函数,所以(2)式的最小值就是(1)式的最大值。 我们用 θ(y w^Tx)) 代替 P(y|x)，得到与参数w有关的式子

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

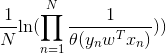
 我们通过最小化上述式子，找出最优的参数w，因此我们可以把上边的式子看做error measure，用sigmoid 函数代替 θ(y w^Tx)) ，我们就可以得到逻辑回归函数的损失函数表达式

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

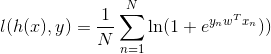
这意味着对于一个数据点而言，损失函数e(h(x_n),y_n) = ln(1+e^y_nwTx_n), 当y_nw ^Tx_n为一个比较大的正数时损失函数就越小，也就是说sign(w ^Tx_n) = y_n,因此我们可以用这个损失函数计算w。所以损失函数的表达式为：

　　　　　　　　　　　　　　　

 

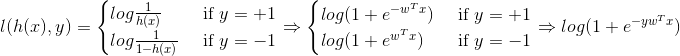
在下一篇文章里我会解释如何用梯度下降的方法来求接这个损失函数

参考资料：<< Learning From Data>> Yaser S . Abu-Mostafa California Institute of Technology