数值优化(1)-最小二乘法

最小二乘法

　　引子：如何求解一个无解方程组Ax=b的解 (Ax=b 是方程组的矩阵表现形式，A为矩阵，x为未知数)

       （例：对于 方程组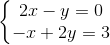而言，它的系数矩阵为 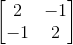，未知数向量为，右侧则有向量，所以方程组用 矩阵表示为）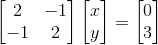

       

　　这个问题听起来很荒谬，实际上这种问题很常见而且必须要解决，所以当Ax=b无解时如何去求解这个方程组，也就是当b不在A的列空间时如何去求解？当A是长方矩阵时，即方程式的数目m大于未知数的数目n。 举个例子，你想要测量一颗卫星的位置，做了一千次测量也就是得到了一千个方程，但是用来确定卫星位置的参数并没有一千个那么多，也许只有六七个。另一个例子是当进行体检时你要为体检者测量脉搏，体检者的脉搏参数是一个未知数，为了确定脉搏频率你只需要测量一次就够，但是为了得到更准确地结果你需要多次测量，但其中可能存在一些误差很大的坏数据。这就是一个很常见的实际问题，当方程式数目特别多的时候b中难免会混入一些坏数据，于是Ax=b就解不出来了，我们有时甚至不知道b中哪个数据有问题。但是b里还包含了很多有效的好数据，所以在求解x时我们需要做的是把b中的坏数据筛选出来，这就用到了线性代数。

       那么如何去求解，我们得到了一些方程如何求出他的最优解，第一种方法是不断去掉一些方程直到剩下一个可逆的方阵然后求出他的解，但该方法的问题是对于所有的测量值我们无从判断那些是有效的好数据那些是无效的坏数据。我们希望利用所有的测量值求出最优解从而得到最完整的信息，那么我们该如何做？假设A是典型的长方形矩阵，我们可以通过消元法来判断它什么时候有解，如果消元法得到的结果是零等于非零，方程组无解。但问题是消元法可以告诉我们方程组是否有解，当我们碰到无解问题时我们该如何做，我们将引入一个非常重要的矩阵A^TA，假设A是一个m×n的长方矩阵，则A^TA为一个n×n的方阵，且他是一个对称矩阵(A^TA)^T=A^T(A^T)^T=A^TA，所以当等式Ax=b无解时，我们可以在等式两边乘上A^T， 将一个“坏”的等式转变成一个“好”的等式A^TAx=A^Tb，这个方程是接下来内容的核心。

 

---

 

（一）正交向量(Orthogonal vector)与投影

   正交是垂直的另一种说法，若向量x与向量y正交(垂直)，则x^Ty=0.

   投影，我们从将b投影到a说起, 为了更好地从几何上理解投影，我画了一个二维的图，首先在a这条线上找到距离b最近的点p，p即b在a上的投影，e为b和p之间的误差，且e垂直于a

　　　　　　　　　　　　　　　　　　　　　　　　

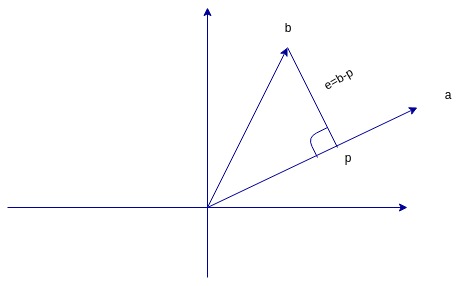
       从图中可知投影p是a的倍数，p=ax (这是投影在一维内的情况，接下来我们会把它推广到高维)，且a垂直于e，即a^T(b-xa)=0. 化简得x=(a^Tb) ⁄ (a^Ta), 所以投影p=ax=a(a^Tb) ⁄ (a^Ta), 在这个式子中矩阵(aa^T) ⁄ (a^Ta)帮助我们完成投影,我们将这个矩阵称之为投影矩阵P。换句话说投影就是由某个矩阵作用在b上使我们得到投影p ，即p = Pb，投影矩阵P=(aa^T) ⁄ (a^Ta)有两个非常重要的性质 1）投影矩阵是对称矩阵即P^T=P 。2）如果投影两次，第二次的结果和第一次的结果是一样的 即P²=P。接下来我们进入高维投影的情况

       在高维投影里我们就不在讨论一条线，而是讨论一个平面甚至三维或n维的子空间，在讨论高维投影之前我们先要明白我们为什么要做投影，这就涉及到我们在最开始提出的问题，等式Ax=b可能没有解即b不在A的列空间里（矩阵列空间的所有向量均为该矩阵中列向量的某种线性组合），我可能有一堆等式，但等式的数量太多比未知数的数量还多造成无解，那么我们该如何解决呢，我们只能求解最接近的那个可解问题。哪个才是最接近的呢？首先Ax总是在A的列空间里，而b却不一定在A的列空间里（即无解的情况），我们可以微调b将它变为A的列空间中最接近初始b的那个向量，所以问题转换成求解Ax=p，p是b在A列空间上的投影, 严格来说应该是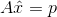, 因为我们现在要求的未知数已经不再是原来的未知数了， 原来是无解的，现在我们求解的是最接近原来问题的可解问题，接下来我们就要在列空间内找到这样一个合适的投影，然后我们就可以求解，这就是我们引入投影的原因。

      接下来我们考虑三维的情况，假设我们有一个平面，和一个不在平面上的b向量，我想要将b投影在平面上，这就是我要解决的问题

　　　　　　　　　　　　　　　　　　　　　　　　　

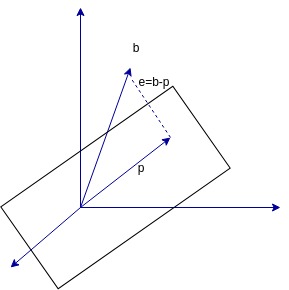
      p是b在平面上的投影,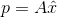，误差向量是e且e垂直于平面，A^Te=A^T(b-p)=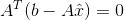, 这是方程的矩阵形式，我们发现平面上的投影方程和直线上的投影方程很相似，对于直线来说矩阵A只有一列，只要将方程里的A换成a这个方程就和前面提到的直线投影的方程一模一样， 本质上都是A^Te=0，解得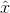=(A^TA)^-1A^Tb，这就是方程的解，投影

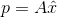 =A(A^TA)^-1A^Tb，投影矩阵为P=A(A^TA)^-1A^T ，投影矩阵可以将向量b投影到他距离A的列空间中的最近的那一点，且该投影矩阵仍然保有如下两个特征 1）P^T=P ，  2）P²=P ，接下来我们考虑如何应用他们

（三）最小二乘

       当我们遇到一个方程组有太多的方程，现在我们需要求解他们的最优解，最常见的例子就是通过最小二乘法拟合一条直线，给定一系列数据点且这些数据点不共线

　　　　　　　　　　　　　　　　　　　　　　 

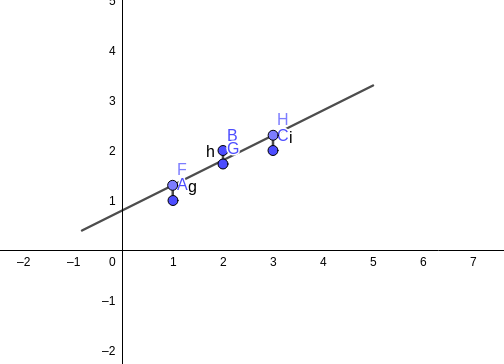
        根据如上图三点找到一条最合适的直线，这三个点分别是A（1,1）, B（2,2）,  C（3,2），显然没有直线能同时经过这三个点因此我们希望求出一条最优直线，这条直线要尽量接近这三个点使得总误差最小，图中这三个点到这条线的误差分别是g，h，i，将这些误差的平方相加 g²+h²+i²，找出最小平方和的解（即最小二乘）也就求出了最优直线。拟合一条直线是统计科学中非常重要的一部分，准确说法应该叫回归，我现在做的就是线性回归分析，我用误差的平方和做为测量总误差的标准，但是最小二乘法有一个问题，如果我再添加一个点，这个点距离其他三个点很远很远，那么在这种情况下原来求得的最优解就不是最优解，因为这条线有一个非常大的误差，第四个点距离我原来求得的最优直线太远了，在统计学中这样的点称之为离群值，我们在处理问题是并不希望看见这样的点，如果有离群值我们希望找到它因为它很可能是个错误数据，所以最小二乘法很容易受到离群值影响 。

        假设没有离群值，只有上图中的三个点，为了求解这条直线首先我们需要构建一个矩阵A，只要找到了矩阵A我们就可以应用我们得到的公式，设这条最优的直线是b=C+Dt,我们需要确定C，D的值。根据这三个点我们可以得到一个方程组 C+D=1, C+2D=2, C+3D=2,注意这个方程组是无解的，如果有解的话表示这三点共线。我们用矩阵方程Ax=b来表示这个方程组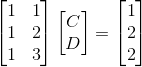， ，这个方程是无解的，但是我们可以求出“最优解”，所谓“最优解”并非原方程Ax=b的解，而是另一个方程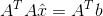的解，（也就是我们前边提到过的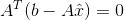）这是最小二乘法的核心方程，虽然Ax=b无解，但当两边都乘以A^T就得到了一个有解的方程，这就可以求出最优解，也就是最理想的投影以及投影矩阵，根据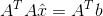，得到   即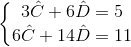,用消元法解得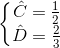, 所以最优直线为y=x/2 + 2/3。这就是最小二乘法，最典型的应用就是拟合一条直线