平衡树Java实现
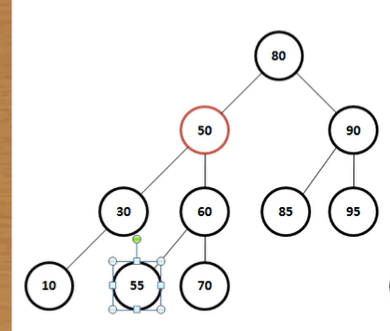
二叉树(平衡树)数据删除
1、没有子节点直接删除就可以
2、如果待删除的节点只有一个子节点,那么直接删除,并用其他节点顶替他
3、如果待删除的节点有两个节点,这种情况就比较复杂,首先找出它的后续节点,处理后续节点与待删除节点的关系,然后在处理后续节点的子节点和被删除节点的子节点之间的关系
import java.util.Arrays;
class BinarytTree<T extends Comparable<T>> {
private class Node {
// 存放Comparable,比较大小
private Comparable<T> data;
//父节点
private Node parent;
//左子树
private Node left;
//右子树
private Node right;
//构造方法负责数据的存储
public Node(Comparable<T> data) {
this.data = data;
}
//适当位置存储
public void addNode(Node newNode) {
//比当前节点小
if (newNode.data.compareTo((T) this.data) <= 0) {
//没有左子树
if (this.left == null) {
//保存左子树
this.left = newNode;
//保存父节点
newNode.parent = this;
} else {
//继续向左判断,继续向下判断
this.left.addNode(newNode);
}
} else {//比根节点数据大
if (this.right == null) {
//保存右子树
this.right = newNode;
newNode.parent = this;
} else {
//继续向右判断,继续向下判断
this.right.addNode(newNode);
}
}
}
//打印树结构
public void toArrayNode() {
//没有左子树 递归调用
if (this.left != null) {
this.left.toArrayNode();
}
BinarytTree.this.returnData[BinarytTree.this.foot++] = this.data;
if (this.right != null) {
this.right.toArrayNode();
}
}
//检查父节点
public boolean containsNode(Comparable<T> data) {
if (data.compareTo((T) this.data) == 0) {
return true;
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.containsNode(data);
} else {
return false;
}
} else {
if (this.right != null) {
return this.right.containsNode(data);
} else {
return false;
}
}
}
//获取要删除的节点对象
public Node getRemovNode(Comparable<T> data) {
//
if (data.compareTo((T) this.data) == 0) {
return this;//找到了
} else if (data.compareTo((T) this.data) < 0) {
if (this.left != null) {
return this.left.getRemovNode(data);
} else {
return null;
}
} else {
if (this.right != null) {
return this.right.getRemovNode(data);
} else {
return null;
}
}
}
}
//所有数据的获取->中序遍历
//*********二叉树操作***********//
//注意根节点 是写在哪里的
private Node root;
private int count;
private Object[] returnData;
private int foot = 0;//脚标
public void add(Comparable<T> data) {
if (data == null) {
throw new NullPointerException("保存数据为空");
}
//所有数据没有节点关系的匹配 那么一定将其包装在Node类中
Node newNode = new Node(data);
//保存节点
if (this.root == null) {
//现在没有根节点,则第一个节点作为根节点
this.root = newNode;
} else {
//保存到合适的节点
this.root.addNode(newNode);
}
//计数
this.count++;
}
//删除处理
public void remove(Comparable<T> data) {
//得到被删除这个数据的父节点,左右两颗子树
Node current = this.root.getRemovNode(data);
if (current != null) {
//没有任何子节点
if (current.left == null && current.right == null) {
//父节点断开引用 检测他是那颗树 断开父节点的 左右子树连接
if (current.parent.left == current) {
current.parent.left = null;
} else {
current.parent.right = null;
}
current.parent = null;
} else if (current.left != null && current.right == null) {
//左子树不为空 那么让他的左子树等于他的父节点的左子树 他的父子树等于他左子树的父子树 更改了
//父节点的指向 不在指向此位置
current.parent.left = current.left;
current.left.parent = current.parent;
} else if (current.left == null && current.right != null) {
//右子树不为空 那么让他的右子树等于他的父节点的右子树 他的父子树等于他右子树的父子树 更改了
//父节点的指向 不在指向此位置
current.parent.right = current.right;
current.right.parent = current.parent;
} else {
//此方式适用于左子树
/*两边都有节点 找被删除的数据中的右子树的最左节点 此数据A(moveNode) 替换要被删除的数据
数据A(moveNode)的父级的left不再有指向
被删除的数据(current)的左子树的parent 指向 A(moveNode)
被删除的数据(current)的parent的left 指向 A(moveNode)
A(moveNode)左子树指向被删除的数据(current)的左子树
A(moveNode)的右子树指向被删除的数据(current)的右子树
current就是被删除的节点*/
Node moveNode = current.right;
if (moveNode.left != null) {
while (moveNode.left != null) {
//还有左边的节点
moveNode = moveNode.left;//一直向左找
}
//确定删除节点的最左边的最小节点
current.parent.left = moveNode;
moveNode.parent.left = null;
moveNode.left = current.left;
moveNode.parent = current.parent;
moveNode.right = current.right;
}else {
current.parent.left = moveNode;
moveNode.left = current.left;
current.left.parent = moveNode;
moveNode.parent = current.parent;
}
}
this.count--;
}
}
public boolean contains(Comparable<T> data) {
if (this.count == 0) {
return false;
}
return this.root.containsNode(data);
}
//以对象数组的形式返回全部数据 没有数据返回Null
public Object[] toArray() {
if (this.count == 0) {
return null;
}
//保存长度为数组长度
this.returnData = new Object[this.count];
this.foot = 0;//脚标清零
this.root.toArrayNode();
return this.returnData;
}
}
class Persons implements Comparable<Persons> {
private String name;
private int age;
public Persons(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "姓名:'" + name + '\'' +
", 年龄:'" + age + '\'';
}
@Override
public int compareTo(Persons o) {
return this.age - o.age;
}
}
public class demotree {
public static void main(String args[]) {
BinarytTree<Persons> btree = new BinarytTree<>();
btree.add(new Persons("小强-80", 80));
btree.add(new Persons("小强-50", 50));
btree.add(new Persons("小强-60", 60));
btree.add(new Persons("小强-30", 30));
btree.add(new Persons("小强-90", 90));
btree.add(new Persons("小强-10", 10));
btree.add(new Persons("小强-55", 55));
btree.add(new Persons("小强-70", 70));
btree.add(new Persons("小强-85", 85));
btree.add(new Persons("小强-95", 95));
btree.remove(new Persons("小强-90", 90));
/* btree.remove(new Persons("小强-70", 70));
btree.remove(new Persons("小强-85", 85));
btree.remove(new Persons("小强-95", 95));*/
System.out.println(Arrays.toString(btree.toArray()));
//System.out.println(btree.contains(new Persons("小强-30", 30)));
}
}
结果
[
姓名:'小强-10', 年龄:'10',
姓名:'小强-30', 年龄:'30',
姓名:'小强-55', 年龄:'55',
姓名:'小强-60', 年龄:'60',
姓名:'小强-70', 年龄:'70',
姓名:'小强-80', 年龄:'80',
姓名:'小强-85', 年龄:'85',
姓名:'小强-90', 年龄:'90',
姓名:'小强-95', 年龄:'95'
]
右子树懒得写了...下次补上




