有一串随机整数列，a1,a2,...an，求数字[0-9]分别出现的次数，比如：[12, 210, 33]输出{'0': 1, '1': 2, '2': 2, '3': 2}，时间和空间复杂度

def get_count():
    dic = {}
    lis_list = []
    lis = []
    data = [12, 210, 33, 90, 88, 222, 115, 666, 677, 4]
    for da in data:
        da = str(da)
        lis_list.append(da)
    res = ''.join(lis_list)
    for i in res:
        lis.append(i)
    for n in lis:  # n是循环的每个数
        dic[n] = lis.count(n)

    return dic


print(get_count())

 

算法(Algorithm)是指用来操作数据、解决程序问题的一组方法，对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，但在过程中消耗的资源和时间却会有很大的区别，主要还是从算法所占用的时间和空间两个维度去考量
时间复杂度：是指执行当前算法所消耗的时间   空间复杂度：是指执行当前算法需要占用多少内存空间
因此评价一个算法的效率主要是看它的时间复杂度和空间复杂度情况，然而有的时候时间和空间却又是鱼和熊掌，不可兼得的，那么我们就需要从中去取一个平衡点

一、时间复杂度

常见的时间复杂度量级有：
常数阶O(1)
对数阶O(logN)
线性阶O(n)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
K次方阶O(n^k)
指数阶(2^n)

上面从上至下依次的时间复杂度越来越大，执行的效率越来越低

1、常数阶O(1)
无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)，如

2、线性阶O(n)
这段代码，for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度

3、平方阶O(n²)
平方阶O(n²) 就更容易理解了，如果把O(n)的代码再嵌套循环一遍，它的时间复杂度就是O(n²)了

 

二、空间复杂度

既然时间复杂度不是用来计算程序具体耗时的，那么我也应该明白，空间复杂度也不是用来计算程序实际占用的空间的，空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，我们用S(n)来定义
空间复杂度比较常用的有：O(1)、O(n)、O(n²)，我们下面来看看：
1、空间复杂度O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为O(1)举例

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)

2、空间复杂度 O(n)
我们先看一个代码：

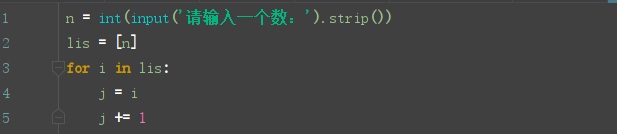
这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)