HuffmanTree,哈夫曼树的原理和c++实现

目录

• 一、什么是哈夫曼树
• 二、构造哈夫曼树
• 三、路径、编码、解码
• 四、代码

一、什么是哈夫曼树

哈夫曼树又称为最优树.

通过权值来构造树,权值越大,离根节点越近

经常用于无损压缩算法

用于需要优化存储空间的场景

原理很简单,不多赘述

具体看百度百科的解释

需要注意 构建哈夫曼树不仅要值,还需要对应的权值

比如越常出现的,权值越大

二、构造哈夫曼树

通过权值来构造哈夫曼树

我画了几个图,具体过程如下

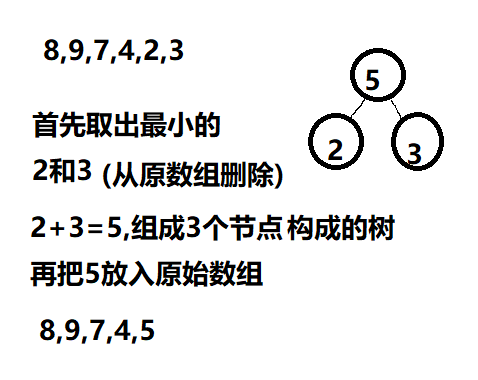
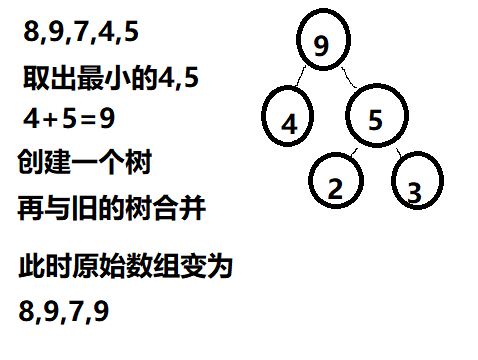
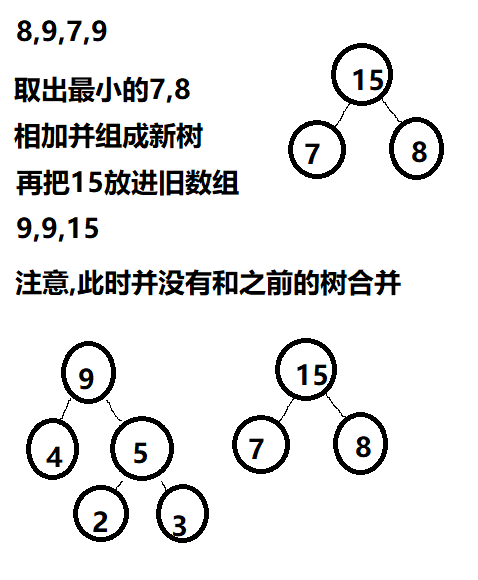
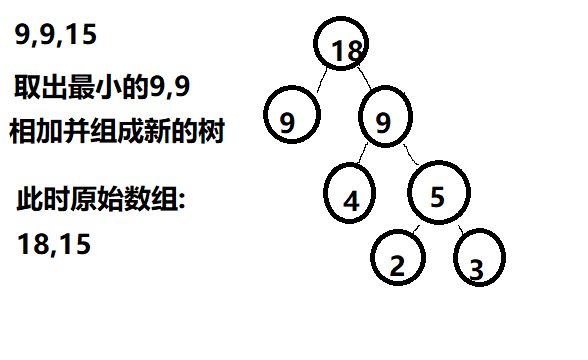
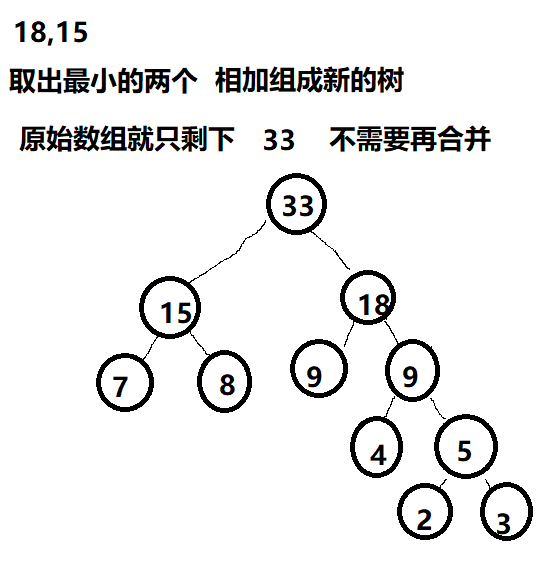
三、路径、编码、解码

上面通过权值构建了哈夫曼树,再将字符与权值对应起来

往左记作0 往右记作1

从根节点到各个叶子节点经过的0和1

就是该节点对应的路径

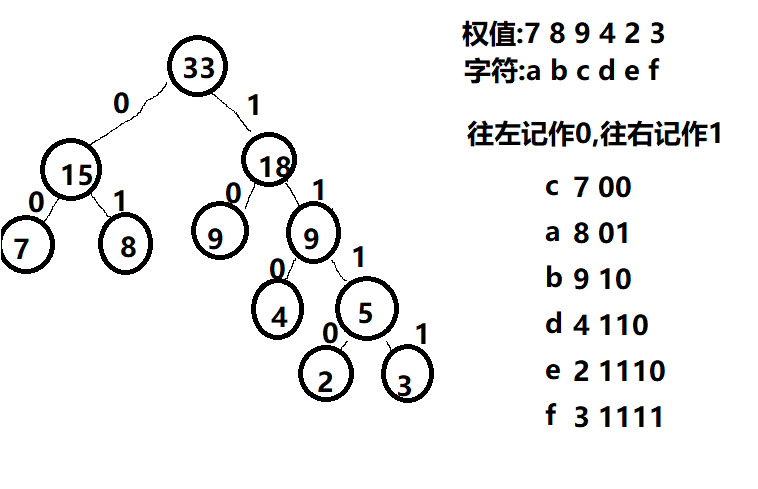
aaabbeaf编码:01010110101110011111

01010110101110011111解码:aaabbeaf

比如一个字符a原来占8位,通过哈夫曼编码后,就只占用2个位

但缺点是 权值较低的 占用字节会比较高,比如e,就占用4个位

四、代码

下面代码只是例子,编码解码并没有真的用位来表示,而是用字符串代替

HuffmanTree.h

#pragma once
#include<queue>
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
class HuffmanTree
{
	struct Node
	{
		int weight;//权值
		Node* left;//左孩子
		Node* right;//右孩子
		char value;//节点值
		string path;//存放路径
	};
	
	//仅用于优先级队列比较
	struct NodeCMP
	{
		bool operator()(Node* a, Node* b)
		{
			return a->weight > b->weight;
		}
	};
private:
	Node* root = nullptr;
	vector<pair<char, string>*>map;
public:
	HuffmanTree(vector<int>& weight, vector<char>& value) {
		createHuffmanTreeNode(weight,value);
		createHuffmanTreePath();
	}
	//初始化节点
	void createHuffmanTreeNode(vector<int>& weight, vector<char>& value) {
		priority_queue<Node*,vector<Node*>, NodeCMP>que;//优先级队列构造树
		for (size_t i = 0; i < weight.size(); i++){
			Node* temp = new Node{ weight[i] ,nullptr,nullptr,value[i] };
			que.push(temp);
		}
		while (que.size() >= 2){
			Node* min1 = que.top();
			que.pop();
			Node* min2 = que.top();
			que.pop();
			Node* node = new Node{ min1->weight + min2->weight,min1,min2 };
			que.push(node);
		}
		root = que.top();
	}
	//初始化路径
	void createHuffmanTreePath() {
		if (root == nullptr)return;
		queue<Node*>que;
		que.push(root);
		while (que.size()){
			Node* temp = que.front();
			que.pop();
			if (temp->left != nullptr) {
				que.push(temp->left);
				temp->left->path.append(temp->path + 0);
			}
			if (temp->right != nullptr){
				que.push(temp->right);
				temp->right->path.append(temp->path + 1);
			}
			if (temp->left == nullptr && temp->right == nullptr) {
				map.push_back(new pair<char, string>(temp->value, temp->path));
			}
		}
	}
	string encode(string data) {
		string result;
		for (size_t i = 0; i < data.size(); i++) {
			char ch = data[i];
			for (size_t j = 0; j < map.size(); j++) {
				pair<char, string>* mapData = map[j];
				if (mapData->first == ch) {
					result.append(mapData->second);
					break;
				}
			}
		}
		return result;
	}
	string decode(string data) {
		string result;
		while (data.size())
		{
			for (size_t i = 0; i < map.size(); i++)
			{
				pair<char, string>* mapData = map[i];
				if (data.find(mapData->second) == 0) {
					result.push_back(mapData->first);
					data = data.substr(mapData->second.size());
					break;
				}
			}
		}
		return result;
	}

};

main.cpp

#include<iostream>
#include<vector>
#includeHuffmanTree.h
int main() 
{
	vector<int>weight = { 8,9,7,4,2,3 };
	vector<char>value = { 'a','b','c','d','e','f'};
	HuffmanTree tree(weight,value);
	string str;
	str = tree.encode(aaabbeaf);
	cout << str << endl;
	str = tree.decode(str);
	cout << str << endl;

	return 0;
}