RS学习1
torch-rechub安装
最新版(推荐)
- git clone https://github.com/datawhalechina/torch-rechub.git
- cd torch-rechub
- python setup.py install
安装过程中遇到问题:python setup.py install
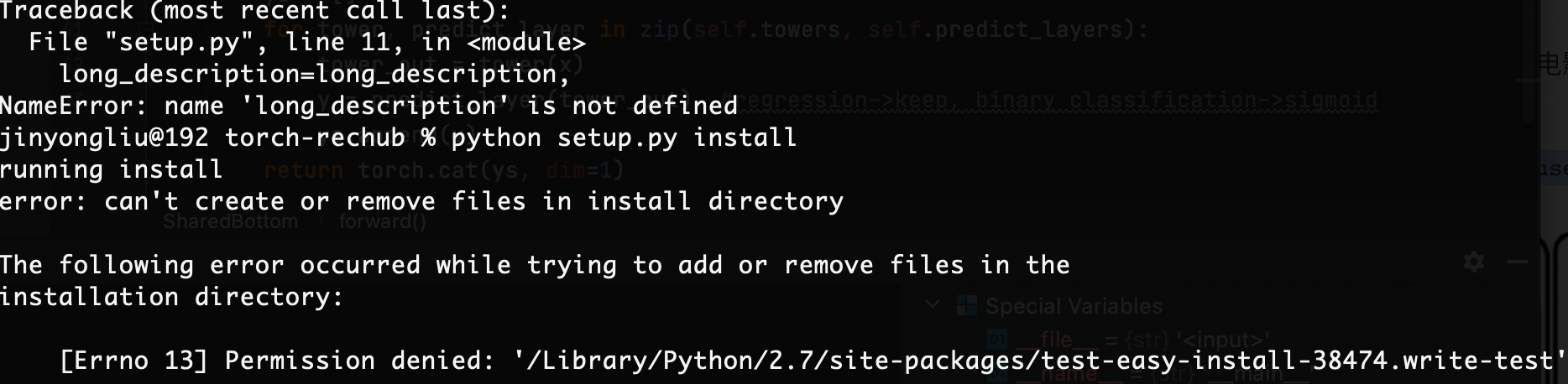
执行python3 setup.py install 成功安装
深度学习推荐算法框架
FM学习
1、FM
前面一章介绍了线性模型和逻辑回归模型,在这些模型中,默认特征之间是不存在交互关系的;对于离散特征(如用户所在城市、商品品牌等),一般是进行one-hot处理,从而会产生大量的稀疏数据。Factorization Machines(FM)模型即是用来解决数据稀疏和特征交叉使用问题的。
1.1 数据说明
如在电影评分系统中的数据,它的每一条记录都包含了哪个用户\(u \in U\)在什么时候\(t \in {\Bbb R}\)对哪部电影\(i \in I\)大了多少分\(r \in \{1,2,3,4,5\}\)这样的信息,假定用户集\(U\)和电影集\(I\)分别为:
\(U = \{Alice(A), Bob(B), Charlie(C),...\}\)
\(I=\{Titanic(TI),Notting \ Hill(NH), Star \ Wars(SW), Star \ Trek(ST),...\}\)
设观测到的数据集\(S\)为:
利用观测数据集\(S\)来进行预测任务的一个实例是:估计一个函数\(\hat y\)来预测某个用户在某个时刻对某部电影的打分行为。有了观测数据集\(S\),构造如下样本:

特征说明如下:
第一部分(对应蓝色框),表示当前评分用户信息,其维度为\(|U|\),该部分分量中,当前电影评分用户所在的位置为1,其他为0。例如在第一条观测记录中\(x_A^{(1)}=1\)
第二部分(对应橙色框),表示当前被评分电影信息,其维度为\(|I|\),该部分的分量中,当前被评分的电影所在的位置为1,其他为0。例如在第一条观测记录中就有\(x_{TI}^{(1)}=1\)
第三部分(对应黄色框),表示当前评分用户评分过的电影信息,其维度为\(|I|\),该部分分量重,被当前用户评论过的所有电影的(设个数为\(n_I\))的位置为\(1/n_I\),其他设为0。如Alice评价过的三部电影TI, NH和SW,因此就有\(x_{TI}^{(1)}=x_{NH}^{(1)}=x_{SW}^{(1)}=1/3\)
第四部分(对应绿色框),表示评分日期信息,其维度为1,用来表示用户评价电影的时间,表示方法是将记录中最早的日期作为基数1,以后每增加一个月就加1
第五部分(对应棕色框)表示当前评分用户评分过的一步电影的信息,其维度为\(|I|\),该部分的分量中,若当前用户评价当前电影之前还评价过其他电影,则将当前用户评价的上一部电影的取值为1,其他为0;若当前用户评价电影之前没有评价过其他电影,则所有分量取值为0。如对于第二条观测记录,Alice评价NH之前评价的是TI,因此有\(x_{TI}^{(2)}=1\)
第六部分(对应很色框)表示打分标签
在一个真实的电影评分系统中,用户的数据\(|U|\)和电影的数据\(|I|\)是很大的,而每个用户参与评论的电影数目则相对很小,可想而知,每一条记录对应的特征向量将会非常稀疏。
1.2 模型方程
给定特征向量\({\tt x}=(x_1,x_2,...,x_n)^T\),线性回归建模时采用的函数是:
从方程中可以看出,各个特征分量\(x_i\)和\(x_j(i\neq j)\)是相互独立的,即\(\hat y(x)\)中仅考虑单个的特征分量,而没有考虑特征分量之间的相互关系,接下来在公式(1)的基础上,将函数\(\hat y\)改写为:
这样便将任意两个互异特征分量之间的关系也考虑进来了。但是这样又会引入大量的稀疏数据,如数据集中没有Alice评价电影Star Trek的记录,如果要直接估计这两者(\(x_A\)和\(x_{ST}\))之间的关系,显然会得到\(w_{A,ST}=0\),即对于观察样本中未出现过交互的特征分量,不能对相应的参数进行估计。在高维稀疏数据场景中,由于数据量的不足,样本中出现未交互的特征分量是很普遍的。
1.3 辅助向量
为了解决数据稀疏的问题,在公式(2)的稀疏\(w_{ij}\)上做文章,引入一个辅助向量
其中\(k \in {\Bbb N}^+\)是超参数,此时\(w_{ij}\)可以改写为:
进一步进行分析可以发现:
因此公式(2)可以进一步简写为:
说明:改进后的交叉项就类似于Word2Vec中根据ID值获取每个word的embedding向量。但是FM中不仅对离散数据取embedding向量,连续数值同样进行了embedding操作。只是在离散数据中,或根据数值的个数生成多个embedding向量,在实际计算中根据离散向量的数值获取对应的embedding;而在连续特征中,只生成一个embedding,在使用该embedding时需要与该特征的具体数据进行相乘。
1.4 代码及其说明
1.4.1 导入包及数据预处理
import torch
from torch import nn
import pandas as pd
import torch.utils.data as Data
import numpy as np
##这里应该会得到两个embedding_dict
def load_data(path):
data = pd.read_csv(path)
sparse_features = ['C' + str(i) for i in range(1, 27)]
dense_features = ['I' + str(i) for i in range(1,14)]
label = data.label.values
label = label.reshape(len(label), 1)
feature_dict = {} #定义一个字典,用于字符转id
data[dense_features] = data[dense_features].fillna(0,)
cnt = 1
features = pd.DataFrame()
indexes = pd.DataFrame()
# 连续特征处理,key值全部为1,value值为原始特征值
for col in dense_features:
values = data.loc[:, col]
values = (values - values.mean()) / values.std()
features = pd.concat([features, values], axis=1)
feature_dict[col] = cnt
indexes = pd.concat([indexes, values * 0 + cnt], axis=1)
cnt += 1
# 离散特征处理,key值为原特征值,value值为1
for col in sparse_features:
values = data.loc[:, col]
uniques = values.unique()
feature_dict[col] = dict(zip(uniques, range(cnt, len(uniques) + cnt)))
indexes = pd.concat([indexes, values.map(feature_dict[col])], axis=1)
# values = 1
features = pd.concat([features, indexes[col]*0+1], axis=1)
cnt += len(uniques)
train_data = {}
train_data['label'] = label
train_data['index'] = indexes.values.tolist()
train_data['features'] = features.values.tolist()
train_data['feat_dim'] = cnt
return train_data
train_data = load_data('./data/criteo_sample.txt')
class FMDataset(Data.Dataset):
def init(self, data):
self.features = data['features']
self.indexes = data['index']
self.labels = data['label']
def __getitem__(self, item):
value, index, label = self.features[item], self.indexes[item], self.labels[item]
return torch.tensor(value, dtype=torch.float), torch.tensor(index, dtype=torch.long), torch.tensor(label,dtype=torch.long)
def __len__(self):
return len(self.labels)
trainDataset = FMDataset(train_data)
train_iter = Data.DataLoader(dataset=trainDataset, batch_size=64, shuffle=True, )
test_iter = Data.DataLoader(dataset=trainDataset, batch_size=64, shuffle=False, )
1.4.2 构建FM模型
class FMModel(nn.Module):
def __init__(self, word_counts, embed_dim):
super(FMModel, self).__init__()
self.embedding = nn.Embedding(word_counts, embed_dim)
self.weight = nn.Embedding(word_counts, 1)
def forward(self, features, index):
# features: [64,39], embed:[64,39,16], weight:[64,39,1]
index = torch.tensor(index)
weights = self.weight(index)
embed = self.embedding(index)
first_embed = torch.mul(weights, features.reshape(weights.shape))
# first_embed = first_embed.squeeze(2)
# first_sum: [batch_size, 1]
first_sum = torch.sum(first_embed, dim=1, keepdim=False)
fm_embed = torch.mul(embed, features.reshape(weights.shape))
square_sum = torch.pow(torch.sum(fm_embed, dim=1, keepdim=True), 2)
sum_square = torch.sum(fm_embed * fm_embed, dim=1, keepdim=True)
# cross_term: [batch_size, 1, embed_dim]
cross_term = square_sum - sum_square
# cross_sum: [batch_size, 1]
cross_sum = 0.5 * torch.sum(cross_term, dim=2, keepdim=False)
return first_sum + cross_sum
model = FMModel(train_data['feat_dim'], 16)
# 对离散特征求embedding,实际上计算的是公式中v的值,k就是embedding的长度。线性部分文章中介绍是用one-hot,对离散值的处理也是分别给每个对应的值构建一个k=1的embedding




