Nadam）

一、牛顿法与拟牛顿法
二、梯度下降法
三、梯度下降法的改进
四、如何选择优化算法

一、牛顿法与拟牛顿法

拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题最有效的方法之一，于20世纪50年代提出。DFP、BFGS和L-BFGS算法都是重要的拟牛顿法。考虑如下无约束的极小化问题$\underset{x} {min} f(x)$，其中${\tt x}=(x_1,x_2,...,x_N)^T \in R^N$这里假设$f$为凸函数，且两阶连续可微，此外记极小问题的解为$x^*$

1、牛顿法

1.1 原始牛顿法（假设f凸函数且两阶连续可导，Hessian矩阵非奇异）

为简单起见，首先考虑$N=1$的简单清醒。牛顿法的基本思想是：在现有极小点估计值的附近对$f(x)$做二阶泰勒展开，进而找到极小点的下一个估计值，设$x_k$为当前的极小点的估计值，则

$\varphi(x)=f(x_k) + f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k)(x-x_k)^2$

表示$f(x)$在$x_k$附近的二阶泰勒展开式（略去了关于$x-x_k$的高阶项），由于求的是最值，由极值必要条件可值

$\varphi'(x)=0$，即 $f'(x)+f''(x)(x-x_k)=0$

从而求得$x = x_k - \frac{f'(x_k)}{f''(x_k)}$

如是若给定初始值$x_0$则可以构造如下的迭代格式$x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)}$

产生序列$\{x_k\}$来逼近$f(x)$的极小点。在一定条件下，$\{x_k\}$可以收敛到$f(x)$的极小点

对于$N>1$的情形，二阶泰勒展开式可以做推广，此时

$\varphi({\tt x})=f({\tt x}_k) +\nabla f({\tt x}_k)({\tt x}-{\tt x}_k)+\frac{1}{2}({\tt x}-{\tt x}_k)^T\nabla^2 f({\tt x}_k)({\tt x}-{\tt x}_k)$

其中$\nabla f$为$f$的梯度向量，$\nabla^2f$为$f$的海森矩阵(Hessian matrix)，其定义分别为：

$\nabla f=\begin{bmatrix} \partial f/ \partial x_1 \\ \partial f/ \partial x_2 \\ \vdots \\\partial f/ \partial x_N \end{bmatrix}$, $\nabla^2 f=\begin{bmatrix} \partial^2 f/ \partial x_1^2 & \partial^2 f/ \partial x_1 \partial x_2 & \cdots & \partial^2 f/ \partial x_1 \partial x_N\\ \partial^2 f/ \partial x_2 \partial x_1 & \partial^2 f/ \partial x_2^2 & \cdots & \partial^2 f/ \partial x_2 \partial x_N \\ \vdots & \vdots & \cdots & \vdots \\\partial^2 f/ \partial x_N \partial x_1 & \partial^2 f/ \partial x_N \partial x_2 & \cdots & \partial^2 f/ \partial x_N^2 \end{bmatrix}$

以下分别将其简记为$g$ 和$H$，特别的，若$f$的混合偏导数可交换次序，即对$\forall i,j, \partial^2 f/\partial x_i \partial x_j = \partial^2 f/\partial x_j \partial x_i$，则海森矩阵$H$为对称矩阵。其中$\nabla f(x_k)$和$\nabla^2f(x_k)$表示$\tt x$去值为$x_k$后得到的实值向量和矩阵，分别记为$g_k$和$H_k$

同样地，由于是求极小点，极值必要条件要求它为$\varphi(x)$的驻点，即$\nabla\varphi(x)=0$，亦即

$g_k + H_k({\tt x}-{\tt x}_k)=0$

进一步，若矩阵$H_k$非奇异，则可解得${\tt x}={\tt x}_k - H_k^{-1}·g_k$，于是给定初始值$\tt x_0$，同样可以构造出迭代格式：${\tt x}_{k+1}={\tt x}_k - H_k^-·g_k$

这就是原始牛顿迭代法，其迭代格式中的搜索方向$d_k=-H_k^{-1}·g_k$称为牛顿方向

算法1.1 牛顿法

给定初值${\tt x}_0$和精度阈值$\epsilon$，并令$k:=0$
计算$g_k$和$H_k$
若$||g_k||<\epsilon$，则停止迭代；否则确定搜索方向$d_k=-H_k^{-1}·g_k$
计算新的迭代点${\tt x}_{k+1} := {\tt x}_k + d_k$
令$k:=k+1$，转至步骤2

当目标函数是二次函数时，由于二阶泰勒展开函数与原目标函数不是接近而是完全相同的二次式，海森矩阵退化成一个常数矩阵，从任一初始值出发，只需一步迭代就可以达到$f(x)$的极小点$x^*$，因此牛顿法是一种具有二次收敛性的算法。至于非二次函数，若函数的二次型较强，或迭代点已进入极小点的邻域，其手链数独也是很快的，这是牛顿法的主要优点。

但原始牛顿法由于迭代公式中没有步长因子，而是定长补偿迭代，对于非二次型目标函数有时会使函数值上升，即出现$f({\tt x}_{k+1}) > f({\tt x}_k)$的情况，这表明原始牛顿法不能保证函数值稳定的下降，在严重的情况下甚至可能造成迭代点$\{{\tt x}_k\}$的发散而导致计算失败

1.2 阻尼牛顿法

为了消除原始牛顿法不能保证函数值稳定的下降的弊病，人们提出了阻尼牛顿法，每次迭代的方向仍采用$d_k$，但每次迭代需沿此方向作一维搜索(line search)，寻求最优的步长因子$\lambda_k$即

$\lambda_k = \underset{\lambda \in R}{argmin}f({\tt x}_k + \lambda d_k)$

算法1.2 阻尼牛顿法

给定初值${\tt x}_0$和精度阈值$\epsilon$，并令$k:=0$
计算$g_k$和$H_k$
若$||g_k||<\epsilon$，则停止迭代；否则确定搜索方向$d_k=-H_k^{-1}·g_k$
利用$\lambda_k = \underset{\lambda \in R}{argmin}f({\tt x}_k + \lambda d_k)$得到步长$\lambda_k$，并令${\tt x}_{k+1} := {\tt x}_k + \lambda_kd_k$
令$k:=k+1$，转至步骤2

注1.1: 算法中涉及到$H_k^{-1}$的计算，实际应用中通常不直接对$H_k$求逆，而是将其转化为求解线性代数方程组$H_kd_k=-g_k$，此时可根据稀疏矩阵$H_k$的形态来选择合适的迭代法，如预条件共轭梯度法(PCG)、代数多重网格法(AMG)等

牛顿法是梯度下降法的进一步发展，梯度法利用目标函数的一阶偏导信息，以负梯度方向作为搜索方向，只考虑目标函数在迭代点的局部性质，而牛顿法不仅使用目标函数的一阶偏导数，还进一步利用了目标函数的二阶偏导数，这样就考虑了梯度变化的趋势，因而能更全面的确定合适的搜索方向，以加快收敛，它具有二阶收敛数独。但牛顿法主要存在以下两个缺点：

1）对目标函数有较严格的要求，函数必须具有连续一、二阶偏导数，海森矩阵必须正定

2）计算相当复杂，除需要计算梯度外，还需要计算二阶偏导数矩阵和它的逆矩阵，计算量和存储量均很大，且均以维度$N$的平方比增加，当N很大时这个问题更加突出。

2、拟牛顿法(如何不用二阶导数构造海森矩阵)

如上所述，牛顿法虽然收敛速度快，但是计算过程中需要计算目标函数的二阶偏导数，计算量较大。而且有时目标函数的海森矩阵无法保持正定，从而使得牛顿法失效。为了客服这两个问题，人们提出了拟牛顿法。这个方法的基本思想是：不用二阶偏导数二构造出近似海森矩阵的正定矩阵，在“拟牛顿”的条件下优化目标函数。不同的构造方法就产生了不同的拟牛顿法

也有人把拟牛顿法翻译成准牛顿法，其实是表示类似于牛顿法的意思，因为只是对算法中用来计算搜索方向的海森矩阵作了近似计算。

2.1 拟牛顿条件（拟牛顿方程，割线条件）

符号约定，使用$B \approx H$，$D\approx H^{-1}$

设经过$k+1$次迭代后得到${\tt x}_{k+1}$，此时将目标函数$f(x)$在${\tt x}_{k+1}$附近作泰勒展开，取二阶近似，得到

$f({\tt x})=f({\tt x}_{k+1}) + \nabla f({\tt x}_{k+1})({\tt x} - {\tt x}_{k+1}) + \frac{1}{2}({\tt x} - {\tt x}_{k+1})^T\nabla^2f({\tt x}_{k+1})({\tt x} - {\tt x}_{k+1})$

两边同时作用一个梯度算子$\nabla$可得：$\nabla f({\tt x}) \approx \nabla f({\tt x}_{k+1}) + H_{k+1}({\tt x} - {\tt x}_{k+1})$

取${\tt x} = {\tt x_k}$，并整理可得：$g_{k+1}-g_k \approx H_{k+1}·({\tt x}_{k+1} - {\tt x}_k)$

若引入记号${\tt s}_k = {\tt x}_{k+1} - {\tt x}_k$，${\tt y}_k = g_{k+1} - g_k$

则2.16可以写成紧凑形式${\tt y}_k \approx H_{k+1}{\tt s}_k$或${\tt s}_k \approx H_{k+1}^{-1}{\tt y}_k$

这就是所谓的拟牛顿法，它对迭代过程中的海森矩阵$H_{k+1}$作约束，因此对$H_{k+1}$做近似的$B_{k+1}$以及对$H_{k+1}^{-1}$做近似的$D_{k+1}$可以将上面的式子改写为${\tt y}_k = B_{k+1}{\tt s}_k$或者${\tt s}_k = D_{k+1}{\tt y}_k （2.21）$

3、拟牛顿法之DFP算法

DFP算法由Davidon于1959年首先提出，后经Fletcher和Powell加以发展和完善，是最早的拟牛顿法，该算法的核心是：通过迭代的方法，对$H_{k+1}^{-1}$做近似，迭代格式为：

$D_{k+1}=D_k + \Delta D_k, k=0,1,2,... （2.22）$

其中的$D_0$通常取为单位矩阵$I$，因此关键是每一步的矫正矩阵$ D\Delta_k$如何构造。

注意迭代格式将嵌套在算法1.2中，因此我们才想$\Delta D_k$可能于${\tt s}_k,{\tt y}_k$和$D_k$发生关联。这么我们采用待定法，即首先将$\Delta D_k$待定称某中形式，然后结合拟牛顿条件（2.21）来进行推导。那将$ \Delta D_k$待定成什么形式呢？这个说起来比较tricky，我们将其待定为：

$\Delta D_k = \alpha \tt uu^T + \beta vv^T （2.23）$

其中，$\alpha, \beta$是待定系数，$\tt u,v \in R^N$为待定向量。从形式上看，这种待定公式至少保证了矩阵$\Delta D_k$的对称性，因为$\tt uu^T$ 和 $ \tt vv^T$都是对称矩阵。将(2.23)带入(2.22)并结合指导条件(2.21)，可得

${\tt s}_k = D_k{\tt y}_k + \alpha{\tt uu^Ty}_k + \beta{vv^Ty}_k (2.24) \\ = D_k{\tt y}_k + {\tt u}(\alpha{\tt u^Ty}_k) + {\tt v}(\beta{v^Ty}_k)=D_k{\tt y}_k + (\alpha{\tt u^Ty}_k){\tt u} +(\beta{v^Ty}_k){\tt v}$

其中括号中的$\alpha{\tt u^Ty}_k$和$\beta{v^Ty}_k$是两个数，不妨做出简单赋值，令

$\alpha{\tt u^Ty}_k=1$和$\beta{v^Ty}_k=-1 （2.26）$

即$\alpha = \frac{1}{{\tt u^Ty}_k}$和$\beta = \frac{-1}{{v^Ty}_k}$，其中${\tt u}$和${\tt v}$仍有待确定

将(2.26)带入(2.25)得到${\tt u} - {\tt v} = {\tt s}_k - D_k{\tt y}_k$

要上式成立，不妨直接取$\tt u=s_k, v=D_ky_k （2.29）$

再将(2.29)带入(2.27)便得$\alpha = \frac{1}{{\tt s_k^Ty}_k}$和$\beta = \frac{-1}{(D_k{\tt y}_k)^T{\tt y}_k}= \frac{-1}{{\tt y}_k^T(D_k){\tt y}_k}$（这里$D_k$是对称的）

这样我们便可以将$\Delta D_k$构造出来了，即$\Delta D_k=\frac{{\tt s}_k{\tt s}_k^T}{{\tt s}_k^T{\tt y}_k} - \frac{D_k{\tt y}_k{\tt y}_k^TD_k}{{\tt y}_k^TD_k{\tt y}_k}$

算法2.1 DFP算法

给定初值${\tt x}_0$和精度阈值$\epsilon$，并令$D_0:=I,k:=0$
确定搜索方向$d_k=-D_k·g_k$(这里$d_k$是定义参数，称作牛顿方向)
利用$\lambda_k = \underset{\lambda \in R}{argmin}f({\tt x}_k + \lambda d_k)$得到步长$\lambda_k$，并令${\tt s}_k = \lambda_kd_k, {\tt x}_{k+1} := {\tt x}_k + {\tt s}_k$
若$||g_{k+1}||<\epsilon$，则算法结束
计算${\tt y}_k = g_{k+1} - g_k$
计算$D_{k+1}=D_k + \Delta D_k = D_k + \frac{{\tt s}_k{\tt s}_k^T}{{\tt s}_k^T{\tt y}_k} - \frac{D_k{\tt y}_k{\tt y}_k^TD_k}{{\tt y}_k^TD_k{\tt y}_k}$
令$k:=k+1$，转至步骤2

4、拟牛顿法之BFGS算法

BFGS算法是以发明者Broyden，Fletcher，Goldfard和Shanno四个人的名字的首字母命名的，比DFP性能更佳，目前它已成为求解无约束非线性优化问题最常用的方法之一。BFGS算法已有较完善的局部收敛理论，对其全局收敛性的研究也取得了重要成果。BFGS算法中核心公式的推导过程于DFP完全类似，只是互换了${\tt s}_k,{\tt y}_k$的位置。

需要注意的是，BFGS算法是直接逼近海森矩阵，即$B_k \approx H_k$，仍采用迭代方法，设迭代格式为：

$B_{k+1}=B_k + \Delta B_k, k=0,1,2,... (2.32)$

其中$B_0$也常取单位矩阵$I$，因此关键是每一步的矫正矩阵$\Delta B_k$如何构造，同样将其待定为

$\Delta B_k = \alpha \tt uu^T + \beta vv^T （2.33）$

将(2.33)带入(2.32)并结合指导条件(2.20)可得${\tt y}_k = B_{k+1}{\tt s}_k = B_k{\tt s}_k + (\alpha{\tt u}^T{\tt s}_k){\tt u}+ (\beta{\tt v}^T{\tt s}_k){\tt v}$

令$\alpha{\tt u^Ts}_k=1$和$\beta{v^Ts}_k=-1 $，以及$u={\tt y}_k, {\tt v}=B_k{\tt s}_k$，可算的即$\alpha = \frac{1}{{\tt y}_k^T{\tt s}_k}$和$\beta = \frac{-1}{{\tt s}_k^TB_k{\tt s}_k}$

从而便可以得到$\Delta B_k=\frac{{\tt y}_k{\tt y}_k^T}{{\tt y}_k^T{\tt s}_k} - \frac{B_k{\tt s}_k{\tt s}_k^TB_k}{{\tt s}_k^TB_k{\tt s}_k}$

算法2.2 BFGS算法(I)

给定初值${\tt x}_0$和精度阈值$\epsilon$，并令$B_0:=I,k:=0$
确定搜索方向$d_k=-B_k^{-1}·g_k$(这里$d_k$是定义参数，称作牛顿方向)
利用$\lambda_k = \underset{\lambda \in R}{argmin}f({\tt x}_k + \lambda d_k)$得到步长$\lambda_k$，并令${\tt s}_k = \lambda_kd_k, {\tt x}_{k+1} := {\tt x}_k + {\tt s}_k$
若$||g_{k+1}||<\epsilon$，则算法结束
计算${\tt y}_k = g_{k+1} - g_k$
计算$B_{k+1}=B_k + \Delta B_k = B_k + \frac{{\tt y}_k{\tt y}_k^T}{{\tt y}_k^T{\tt s}_k} - \frac{B_k{\tt s}_k{\tt s}_k^TB_k}{{\tt s}_k^TB_k{\tt s}_k}$
令$k:=k+1$，转至步骤2

算法2.2中步2通常是通过求解线性代数方程组$B_kd_k=-g_k$来进行，然而更一般的做法是通过步6的递推关系应用Sherman-Morrison公式，直接给出$B_{k+1}^{-1}$和$B_k^{-1}$之间的关系式

$B_{k+1}^{-1}= (I-\frac{s_ky_k^T}{y_k^Ts_k})B_k^{-1}(I-\frac{y_ks_k^T}{y_k^Ts_k}) + \frac{s_ks_k^T}{y_k^Ts_k} \\=B_k^{-1} + (\frac{1}{s_k^ty_k} + \frac{y_k^TB_k{-1}y_k}{(s_k^Ty_k)^2})s_ks_k^T -\frac{1}{s_k^Ty_k}(B_k^{-1}y_ks_k^T+s_ky_k^TB_k^{-1}) (2.39)$

Sherman-Morrison公式：设$A \in R^n$为非奇异方阵，$\text{u,v} \in R^n$，若$1+{\tt v}^TA^{-1}{\tt u} \neq 0$，则有：

$(A+{\tt uv}^T)^{-1} = A^{-1} - \frac{A^-1{\tt uv}^TA^{-1}}{1+{\tt v}^TA^{-1}{\tt u}}$

且为了避免出现矩阵求拟的符号，我们统一将$B_i^{-1}$用$D_i$替换，整个算法不再需要求解线性代数方程组，由矩阵-向量运算就可以完成了

算法2.2 BFGS算法(II)

给定初值${\tt x}_0$和精度阈值$\epsilon$，并令$D_0:=I,k:=0$
确定搜索方向$d_k=-B_k^{-1}·g_k$(这里$d_k$是定义参数，称作牛顿方向)
利用$\lambda_k = \underset{\lambda \in R}{argmin}f({\tt x}_k + \lambda d_k)$得到步长$\lambda_k$，并令${\tt s}_k = \lambda_kd_k, {\tt x}_{k+1} := {\tt x}_k + {\tt s}_k$
若$||g_{k+1}||<\epsilon$，则算法结束
计算${\tt y}_k = g_{k+1} - g_k$
计算$D_{k+1} = (I-\frac{s_ky_k^T}{y_k^Ts_k})D_k(I-\frac{y_ks_k^T}{y_k^Ts_k}) + \frac{s_ks_k^T}{y_k^Ts_k}$（与DFP算法的区别点）
令$k:=k+1$，转至步骤2

5、L-BFGS算法

在BFGS算法中，需要用到一个$N \times N$的矩阵$D_k$，当N很大时，存储这个矩阵将变得很耗计算机资源，L-BFGS算法不再存储完整的矩阵$D_k$，而是存储计算过程中的向量序列$\{s_i\},\{y_i\}$，需要矩阵$D_k$时，利用向量序列$\{s_i\},\{y_i\}$的计算来代替。而且向量序列$\{s_i\},\{y_i\}$也不是所有的都存，而是固定存最新的m个（参数m时可指定参数），每次计算$D_k$时，只利用最新的m个$\{s_i\},\{y_i\}$。显然这样以来我们将存储由原来的$O(N^2)$降到了$O(mN)$

由算法2.3的更新公式$D_{k+1} = (I-\frac{s_ky_k^T}{y_k^Ts_k})D_k(I-\frac{y_ks_k^T}{y_k^Ts_k}) + \frac{s_ks_k^T}{y_k^Ts_k}$，可令$\rho_k=\frac{1}{y_k^ts_k}, V_k=I-\rho_ky_ks_k^T$，于是更新公式可以改写为：$D_{k+1}=V_k^TD_kV_k + \rho_ks_ks_k^T （2.43）$

如果给定初始矩阵$D_0$，则利用（2.43）依次可得

$D_0=V_0^TD_0V_0 + \rho_0s_0s_0^T$

$D_1=V_1^TD_1V_1 + \rho_1s_1s_1^T = V_1^T(V_0^TD_0V_0 + \rho_0s_0s_0^T)V_1 + \rho_1s_1s_1^T$

...

$D_{k+1}= (V_k^TV_{k-1}^T...V_1^TV_0^T)D_0(V_0V_1...V_{k-1}V_k) \\+(V_k^TV_{k-1}^T...V_2^Tv_1^T)(\rho_0s_0s_0^T)(V_1V_2...V_{k-1}V_k) \\+...\\+(V_k^TV_{k-1}^T)(\rho_{k-2}s_{k-2}s_{k-2}^T)(V_{k-1}V_k)\\+V_k^T(\rho_{k-1}s_{k-1}s_{k-1}^T)V_k \\+\rho_ks_ks_k^T$

由上式可见，计算$D_{k+1}$需要用到$\{s_i,y_i\}_{i=0}^k$，因此若从$s_0,y_0$开始连续的存储m组的话，只能存储到$s_{m-1}, y_{m-1}$，也就是说只能依次计算$D_1,D_2,...,D_m$，那么$D_{m+1}, D_{m+2}$该如何计算呢？

如果一定要丢掉一些向量，那么肯定优先考虑那些最早生成的限量，具体来说，计算$D_{m+1}$时，我们保存$\{s_i,y_i\}_{i=1}^m$，丢掉了$\{s_0,y_0\}$，计算$D_{m+2}$时，我们保存$\{s_i,y_i\}_{i=2}^{m+1}$，丢掉$\{s_1,y_1\}$...

但是丢掉一些向量后就只能近似计算了，当$k+1>m$时，仿照(2.44)可以构造近似公式

$D_{k+1}= (V_k^TV_{k-1}^T...V_{k-m+2}^TV_{k-m+1}^T)D_0(V_{k-m+1}V_{k-m+2}...V_{k-1}V_k) \\+(V_k^TV_{k-1}^T...V_{k-m+2}^Tv_{k-m+2}^T)(\rho_0s_0s_0^T)(V_{k-m+2}V_{k-m+3}...V_{k-1}V_k) \\+...\\+(V_k^TV_{k-1}^T)(\rho_{k-2}s_{k-2}s_{k-2}^T)(V_{k-1}V_k)\\+V_k^T(\rho_{k-1}s_{k-1}s_{k-1}^T)V_k \\+\rho_ks_ks_k^T$

若引入$\hat m = min{k, m-1}$，则还可以合并写成（$k+1\leq m$也成立）

$D_{k+1}= (V_k^TV_{k-1}^T...V_{k-\hat m+2}^TV_{k-\hat m+1}^T)D_0(V_{k-\hat m+1}V_{k-\hat m+2}...V_{k-1}V_k) \\+(V_k^TV_{k-1}^T...V_{k-\hat m+2}^Tv_{k-\hat m+2}^T)(\rho_0s_0s_0^T)(V_{k-\hat m+2}V_{k-\hat m+3}...V_{k-1}V_k) \\+...\\+(V_k^TV_{k-1}^T)(\rho_{k-2}s_{k-2}s_{k-2}^T)(V_{k-1}V_k)\\+V_k^T(\rho_{k-1}s_{k-1}s_{k-1}^T)V_k \\+\rho_ks_ks_k^T$

算法2.4 （$D_k·g_k$的快速算法）

Step1 初始化

初始化 $\delta = \begin{cases} 0 & k\leq m \\ k-m & k>m\end{cases}$； $L = \begin{cases} k & k\leq m \\ m & k>m\end{cases}$； $q_L=g_k$

Step2 后向循环

FOR i = L-1, L-2, ...,1,0 DO

{

\[\begin{array}{l} j=i+\delta \\ \alpha_i = \rho_js_j^Tq_{i+1}, \alpha_i需要保存下来，前向循环使用 \\ q_i = q_{i+1} - \alpha_iy_j \end{array} \]

}

Step3 前向循环

$r_0$ = $D_0 · q_0$

FOR i = L-1, L-2, ...,1,0 DO

{

\[\begin{array}{l} j=i+\delta \\ \beta_i = \rho_jy_j^Tt_{i} \\ r_{i+1} = r_i + (\alpha_i - \beta_i)s_j \end{array} \]

}

最后算出的$r_L$即为$H_k · g_k$的值

二、梯度下降法

在求解节气学习的模型参数，即无约束优化问题时，梯度下降法是最常用的方法之一，另一种常用的方法是最小二乘法。

2.1 梯度

在微积分里面，对多元函数的参数求偏导，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数$f(x,y)$分别对$x,y$求偏导的梯度向量就是$(\partial f/\partial x, \partial f/\partial y)$，简称$grad f(x,y)$或者$\nabla f(x,y)$。对于在点$(x_0,y_0)$的具体梯度向量就是$\nabla f(x_0,y_0)$。

这个梯度集合意义上讲，就是函数变化最快的地方，具体来说对于函数$f(x,y)$在点$(x_0,y_0)$，沿着梯度向量的方向就是$\nabla f(x_0,y_0)$的方向是$f(x,y)$增加最快的地方。或者说沿着梯度向量的方向，更容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是$-\nabla f(x_0,y_0)$的方向，梯度减少最快，也就是最容易找到函数的最小值。

2.2 梯度下降与梯度上升

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值，反过来，如果我们需要求解损失函数的最大值，就需要使用梯度上升法来迭代了。梯度下降法和梯度上升法是可以互相转化的。

2.3 梯度下降法算法详解

首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

2.3.1 梯度下降法的相关概念

1）步长(Learning rate)：步长决定了在梯度下降的迭代过程中，每一步梯度负方向前进的长度（类似于阻尼牛顿法中的阻尼系数）。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

2）特征(feature)：指的是样本中输入部分，比如两个单特征的样本$(x^{(0)},y^{(0)}),(x^{(1)},y^{(1)})$，牛顿法中就是因为特征值过多可能会导致二阶梯度计算复杂，所以引入了拟牛顿法。

3）假设函数(hypothesis function)：在监督学习中，为了拟合输入样本，而使用的假设函数，记为$h_\theta(x)$，就是假设的函数形式，如$h_\theta(x)=\theta_0 + \theta_1x$

4）损失函数(loss function)：为了评估模型拟合的好坏，通常损失函数来度量拟合程度。分类算法中常用的损失函数是交叉熵损失，回归算法中使用的是平方损失，如$J(\theta_0, \theta_1)=\sum_{i=1}^m(h_\theta(x_i)-y_i)^2$

2.3.2 梯度下降法的详细算法（代数法和矩阵法）

梯度下降法的代数描述

1.先决条件：确认模型的假设函数和损失函数

比如线性回归，假设函数表示为$h_\theta(x_1,x_2,...,x_n)=\theta_0 + \theta_1x_1 + ... + \theta_nx_n$

损失函数为：$J(\theta_0, theta_1,...,\theta_n) = \frac{1}{2m}\sum_{j=1}^m(h_\theta(x_0^{(j)}, x_1^{(j)},...,x_n^{(j)}), y_j)^2$

2.算法相关参数初始化

主要是初始化$\theta_0, \theta_1,...,\theta_n$，算法终止距离$\epsilon$以及步长$\alpha$

3.算法过程：

确定当前位置的损失函数的梯度，对于$\theta_i$其梯度表达式为：$\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1,...,\theta_n)$

用步长乘以损失函数的梯度，得到当前位置下降的距离：$\alpha \frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1,...,\theta_n)$

确定是否所有的$\theta_i$梯度下降的距离都小于$\epsilon$，如果小于$\epsilon$则算法终止，当前所有的$\theta_i (i=0,1,...,n)$。否则进入步骤4

更新所有的$\theta$，对于$\theta_i$其更新表达式为：$\theta_i = \theta_i - \alpha \frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1,...,\theta_n)$

以线性回归的例子来具体描述，假设样本$(x_1^{(0)},x_2^{(0)},...,x_n^{(0)},y_0),(x_1^{(1)},x_2^{(1)},...,x_n^{(1)},y_1),...,(x_1^{(m)},x_2^{(m)},...,x_n^{(m)},y_m)$

损失函数为：$J(\theta_0, theta_1,...,\theta_n) = \frac{1}{2m}\sum_{j=1}^m(h_\theta(x_0^{(j)}, x_1^{(j)},...,x_n^{(j)}), y_j)^2$

对$\theta_i$求偏导：$\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1,...,\theta_n)=\frac{1}{m}\sum_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

由于样本中没有$x_0$，上式令所有的$x_0^j$为1

更新参数：$\theta_i = \theta_i - \alpha \frac{1}{m}\sum_{j=0}^m(h_\theta(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

上文中加上$\frac{1}{m}$是为了好理解，由步长为常数，所有$\alpha \frac{1}{m}$可以合并到，使用一个常数表示即可(这就是为什么在设置学习率的时候，往往设置的很小，是因为在原学习率的基础上需要再除以一个样本数)

梯度下降法的矩阵方式描述

1.先决条件

同上一节，但是可以简化为矩阵形式$h_\theta(X) = X\theta$，其中$h_\theta(X)$为$m \times 1$的向量，$\theta$为$(n+1) \times 1$的向量，$X$为$m \times (n+1)$维的矩阵。m代表样本个数，n+1代表样本的特征数

损失函数为:$J(\theta)=\frac{1}{2}(X\theta-Y)^T(X\theta-Y)$，其中Y是样本输出向量，维度为$m \times 1$

2.算法相关参数初始化

同上一节

3.算法过程

确定当前损失函数的梯度$\frac{\partial J(\theta)}{\partial \theta}$

用步长乘以损失函数的梯度，得到当前位置下降的距离：$\alpha \frac{\partial}{\partial\theta}J(\theta)$

确定$\theta$中每个值的距离都小于$\epsilon$，如果小于$\epsilon$则算法终止，当前所有的$\theta_i (i=0,1,...,n)$。否则进入步骤4

更新$\theta$向量：$\theta = \theta - \alpha \frac{\partial}{\partial\theta}J(\theta)$

还是上面的例子，其中对$\theta$向量的偏导数计算为$\frac{\partial}{\partial\theta}J(\theta)=X^T(X\theta-Y)$

更新：$\theta = \theta - \alpha \frac{\partial}{\partial\theta}J(\theta) = \theta - \alpha X^T(X\theta - Y)$

3.3 梯度下降的算法调优

1）算法的步长选择，可以先大后小。（好像有一个专门的算法，初始时先快速增大，然后再持续减小，查资料）

2）算法参数的初始值选择。

3）特征归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化。（经常看到的一个图，神经网络中为什么要对数据做归一化）

4.梯度下降法和其他无约束优化算法的比较

在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

　　　　梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

　　　　梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

三、梯度下降法的改进

3.1 优化算法通用框架

首先定义：待优化参数$\theta$，目标函数$f(\theta)$，初始学习率$\alpha$，而后开始进行迭代优化，在每个迭代步骤：

1.计算目标函数关于当前参数的梯度 $g_t = \nabla f(\theta_t)$

2.根据历史梯度计算一阶动量和二阶动量: $m_t = \phi(g_1, g_2, ...,g_t), V_t=\psi(g_1,g_2,...,g_t)$

3.计算当前时刻的下降梯度:$\eta_t = \alpha · m_t / \sqrt{V_t}$ (相当于SGD中介绍的往下走的距离)

4.根据夏季那个梯度进行更新$\theta_{t+1} = \theta_t - \eta_t$

注：这里的一阶动量和二阶动量与牛顿法中的一阶导数和二阶导数的概念容易混淆；一阶导数就是梯度，而一阶动量和二阶动量是根据历史梯度计算出来的

根据上述框架，来看看SGD解释，$\theta = \theta - \alpha \frac{\partial}{\partial\theta}J(\theta)$，其中:

下降梯度可以描述为：$\eta_t=\alpha ·g_t$

根据通用框架：$\eta_t = \alpha · m_t / \sqrt{V_t}$

因此可令$m_t=g_t, V_t=I^2$

3.2 SGD with Momentum

为了抑制SGD的震荡，Momentum认为梯度下降过程中可以加入惯性。下坡的时候，如果发现是陡坡，就利用惯性跑的快一些，SGDM（SGD with Momentum）在SGD的基础上引入了一阶动量，

$m_t = \beta_1m_{t-1} + (1-\beta_1)·g_t$

一阶动量是各个时刻梯度方向的指数移动平均值，约等于$1/(1-\beta_1)$个时刻的梯度向量的平均值。也就是说t时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定。$\beta_1$的经验值为0.9，这就意味着下降方向主要是此前积累的下降方向，并略微偏向当前时刻的下降方向。可以想象高速公路上汽车转弯，在高速向前的同时略微偏向，急转弯时要出事的。

3.3 SGD with Newterov Acceleration

SGD还有一个问题时困在局部最优的沟壑里面震荡。想象一下你走到一个盆地，四周都是略高的小山，你觉得没有下坡的方向，那就只能待在这里了。可是如果你爬上高地，就会发现外面的世界还很广阔。因此，我们不能停留在当前位置去观察未来的方向，而要向前一步、多看一步、看远一些。

NAG的全称Nesterov Accelerated Gradient是在SGDM的基础上进一步改进，主要是针对梯度的改进。不再计算当前位置的梯度方向，而是按照累积动量走了一步，那个时候下降的方向。即计算梯度的时候，将动量考虑了进来。

$g_t = \nabla f(\theta_t - \alpha m_{t-1}/\sqrt{V_{t-1}})$

在此梯度的基础上，重新计算一阶动量和二阶动量

3.3 AdaGrad

二阶动量的出现，意味着“自适应学习率”优化算法时代的到来。SGD及其变种以同样的学习率更新每个参数，但神经网络往往包含大量的参数，这些参数并不是总会用得到，对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被耽搁样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的的样本本身多学一些，即学习速率大一些。利用二阶动量，获取每个维度上迄今为止所有梯度值的平方和：

$V_t = \sum_{j=1}^t g_j^2$

根据$\eta_t = \alpha · m_t / \sqrt{V_t}$，实际上此时的学习率已经变为$\alpha / \sqrt{V_t}$（历史累积梯度越大，对应维度的学习率就越小）。这一方法在系数数据场景下表现非常好，但也存在一些问题：因为 $\sqrt{V_t}$是单调递增的，会使得学习率单调递减至0，可能会使训练过程提前结束，即便后续还有数据也无法学到必要的知识。

3.4 AdaDelta/RMSProp

由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略，不累积全部历史梯度，而只关注过去一段时间穿够的下降速度。这就是AdaDelta名称中Delta的来历。

SGDM中有介绍，指数移动平均大约就是过去一段时间的平均值，因为我们用这一方法来计算二阶累积动量：

$V_t = \beta_2 * V_{t-1} + (1-\beta_2)g_t^2$

这样就避免了二阶动量的持续累积，导致训练过程提前结束的问题了。

注意：AdaDelta不需要单独设置学习率

RMSprop其实是Adadelta的一种特殊情况，其依然靠的是全局的学习率

3.5 Adam

前面介绍，SGDM在SGD的基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量，把一阶和二阶动量都用起来，就是Adam了，Adaptive + Nomentum

一阶动量：$m_t = \beta_1 ·m_{t-1} + (1- \beta_1) ·g_t$

二阶动量：$V_t =\beta_2*V_{t-1}*(1-\beta_2)g_t^2$

实际使用过程中，取$\beta_1 = 0.9, \beta_2 = 0.999$，初始化$m_0 = 0, V_0 = 0$

$m_t$大，$V_t$大，梯度大且稳定，遇到一个明显的大坡，前进方向明确

2)$m_t$大，$V_t$小，不可能出现

3)$m_t$小，$V_t$大，梯度不稳定，可能遇到一个峡谷，窑易引起反弹震荡

4)$m_t$小，$V_t$小，梯度趋于零，可能到这局部最低点，也可能走到一片坡度假缰的平地，此时要避免陷入平原( plateau )

3.6 Nadam

在Nadam是在Adam的基础上增加了Nestreov，体现在计算梯度的公式上：

$g_t = \nabla f(\theta_t - \alpha m_{t-1}/\sqrt{V_{t-1}})$

四、如何选择优化算法

4.1 Adam存在的几个问题

4.1.1 可能不收敛

二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得 $V_t$ 可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

对二阶动量进行修正$V_t = max(\beta_2 V_{t-1}+(1-\beta_2)g_t^2, V_{t-1})$，这样就保证了$||V_t|| \geq ||V_{t-1}||$，从而使学习率单调递减。

4.1.2 可能错过全局最优解

同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。

4.1.3 小结

理解数据对于设计算法的必要性。优化算法的演变历史，都是基于对数据的某种假设而进行的优化，那么某种算法是否有效，就要看你的数据是否符合该算法的胃口了。

4.2 Adam+SGD

需要注意解决两个问题：

切换算法以后用什么样的学习率？——Adam用的是自适应学习率，依赖的是二阶动量的累积，SGD接着训练的话，用什么样的学习率？
什么时候切换优化算法？——如果切换太晚，Adam可能已经跑到自己的盆地里去了，SGD再怎么好也跑不出来了。

4.2.1 切换算法后用什么样的学习率

Adam的下降方向是：$\eta_t^{Adam} = (\alpha /\sqrt{V_t})·m_t$

SGD的下降方向是：$\eta_t^{SGD} = \alpha^{SGD}·g_t$

$\eta_t^{SGD}$必定可以分解为$\eta_t^{Adam}$所在方向及其正交方向上的两个方向的和。那么其在$\eta_t^{Adam}$上的投影就意味着SGD在Adam算法决定的下降方向上前进的距离，而在$\eta_t^{Adam}$的正交方向上的投影是SGD在自己选择的修正方向上前进的距离。

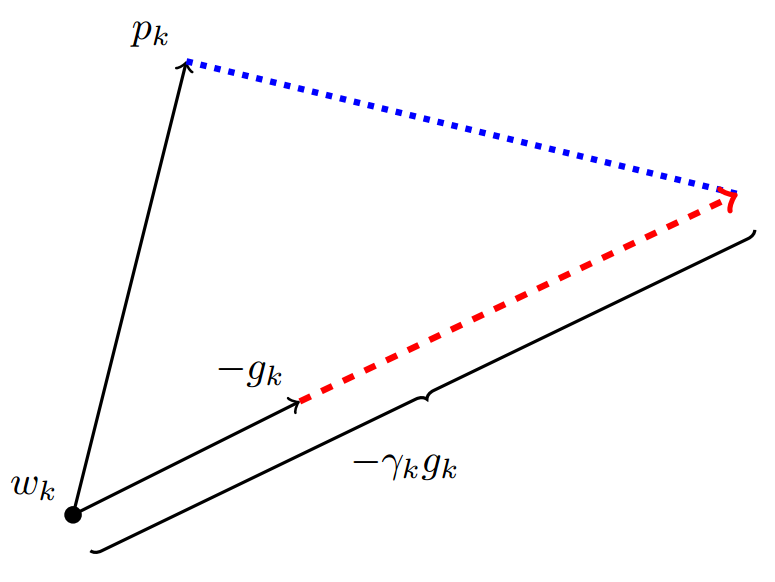
preview

如果SGD要走完Adam未走完的路，那就首先要结果Adam的大旗，并沿着$\eta_t^{Adam}$方向走一步，而后再沿着其正交方向走相应的一步。

这样我们就知道该如何确定SGD的步长了--SGD在Adam下降方向上的正交投影，应该正好等于Adam的下降方向（含步长），也即：$proj_{\eta_t^{SGD}} = \eta_t^{Adam}$

解这个方程可以得到接续进行SGD的学习率：$\alpha_t^{SGD}=((\eta_t^{Adam})^T\eta_t^{Adam})/((\eta_t^{Adam})^Tg_t)$

为了减少噪声的影响，作者使用移动平均值来修正对学习率的预估，即：

$\lambda_t^{SGD} = \beta_2· \lambda_{t-1}^{SGD} + (1-\beta_2)·\alpha_t^{SGD}$， $\tilde \lambda_t^{SGD}=\lambda_t^{SGD}/(1-\beta_2^t)$

这里直接服用了Adam的$\beta_2$参数

4.2.2 什么时候切算法

当SGD的相应学习率的移动平均值基本不变的时候，即$|\tilde \lambda_t^{SGD} - \alpha_t^{SGD}| < \epsilon$，每次迭代完都会计算一下SGD接班人的相应学习率；如果发现基本稳定了，那就使用SGD，并以$\tilde \lambda_t^{SGD}$为学习率继续前进

4.3 优化算法常用tricks

各大算法孰优孰劣并无定论，如果刚入门，优先考虑SGD+Nesterov Momentum或者Adam
选择你熟悉的算法--这样就可以更加熟练的利用经验进行调参
充分了解你的数据--如果数据非常系数，那么优先考虑自适应学习率的算法
根据你的需求来选择--再模型设计实验过程中，要快速验证新模型的效果，可以先用Adam进行快速实验优化，在模型上线或者结果发布前，可以用精调的SGD进行模型的极致优化
先用小数据集进行实验
考虑不同算法的组合--先用Adam进行快速下降，而后再换到SGD进行充分的调优
数据集一定要充分的打散(shuffle)--这样再使用自适应学习率算法的时候，可以避免某些特征几种出现，而导致的有时学习过度、有时学习不足，使得下降方向出现偏差的问题
训练过程中持续监控训练数据和验证数据上的目标函数值以及精度或者AUC等指标变化情况，避免出现过拟合
指定一个合适的学习率衰减策略--可以使用定期衰减，比如每过多少个epoch就衰减一次，或者利用精度或AUC等性能指标来监控，当测试集上的指标不变或者下跌时，就降低学习率。

4.4 为什么深度学习不使用牛顿法或者拟牛顿法

原因1: 牛顿法需要用到梯度和Hessian矩阵，这两个都难以求解。因为很难写出深度神经网络拟合函数的表达式，遑论直接得到其梯度表达式，更不要说得到基于梯度的Hessian矩阵了。

原因2: 即使可以得到梯度和Hessian矩阵，当输入向量的维度N较大时，Hessian矩阵的大小是N×N，所需要的内存非常大。

原因3: 在高维非凸优化问题中，鞍点相对于局部最小值的数量非常多，而且鞍点处的损失值相对于局部最小值处也比较大。而二阶优化算法是寻找梯度为0的点，所以很容易陷入鞍点。

posted @ 2021-07-22 23:15 liujy1 阅读(1385) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

liujy1