逻辑回归整理

0、概述

  本文的主要整理思路为：线性回归-->广义线性回归-->逻辑回归。线性回归是对描述问题的特征进行线性加权的过程，线性模型只能描述输入变量的线性关系，模型具有极大的局限性。为了提升模型性能，需要引入激活函数，罗辑回归即是一种引入了特定激活函数的线性回归模型。

  文中还对一些容易混淆的概念进行了对比说明，如基函数和激活函数，Logistic分布和Sigmoid函数

1、线性模型

  线性模型一般用于解决回归问题，最简单模型是输入变量的线性组合

\[f(w,x)=w_0+w_1x_1+...+w_Dx_D, 其中x=(x_1,...,x_D)^T \tag{1} \]

上式是参数\(w\)的一个线性函数，同时也是输入变量\(x_i\)的一个线性函数，这给模型带来的极大的局限性。

  因此扩展模型的类别，将输入变量的固定的非线性函数进行线性组合，此时的模型也被称为广义线性模型即GLM，形式为：

\[f(w,x)=w_0+\underset{j=1}{\overset{M-1} \sum} w_j\phi_j(x) \tag{2} \]

其中\(\phi_j(x)\)​​​被称为基函数(可以作为一种特殊的激活函数,如径向基函数)，通常设置一个额外的虚“基函数”\(\phi_0(x)=1\)，此时函数可以写为：

\[f(w,x)=\underset{j=0}{\overset{M-1} \sum} w_j\phi_j(x) \tag{3} \]

通过使用非线性基函数，能让函数\(y(x,w)\)​成为输入\(x\)​的一个非线性函数，但是该函数还是\(w\)​的线性函数，因此还是被称为线性模型。

  线性回归假设误差是符合高斯分布的，即：

\[y=f(x,w)+\epsilon \tag{4} \]

因为\(\epsilon\)服从高斯分布，因此可以使用最小化\(\epsilon^2\)的方法来计算最优参数，即最小化误差：

\[Loss = \sum_{n=1}^N(y_n - f(x_n,w))^2 = \sum_{n=1}^N((y_n-w^T\phi(x_n))^2 \propto \frac{1}{2}\sum_{n=1}^N((t_n-w^T\phi(x_n))^2\tag{5} \]

1.1 说明基函数与激活函数的区别

  在很多文献中都出现了基函数和激活函数，实际上两者是不相同的。基函数只是将输入数据\(x\)进行非线性变换，对于参数\(w\)而言仍然是线性函数，基函数常见于SVM中；而激活函数使用更广泛的对\(w\)和\(x\)同时进行非线性变化。

常见的基函数有：

1. 幂指函数的形式：\(\phi_j(x)=x^j\)
2. 样条函数：将输入空间切分成若干个区域，然后对于每个区域用不同的多项式函数拟合
3. 高斯函数：\(\phi_j(x)=exp(-\frac{(x-\mu)^2}{2\gamma^2})\)​
4. sigmoid基函数：\(\phi(x)=\sigma(\frac{x-\mu}{\gamma})\)​​，其中\(\sigma(a)=\frac{1}{1+exp(-a)}\)​

常见的激活函数有：

1. sigmoid函数：\(g(z)=\frac{1}{1+e^{-z}}，其中z=w_0+w_1x_1+...+w_Dx_D\)
2. relu函数：

后续将介绍的逻辑回归，实际上就是指定激活函数后的一个广义线性模型。

1.2 正则化

 过拟合问题是几乎任何机器学习模型都会遇到的问题，为了抑制过拟合的影响，一种常见的方法是在损失函数中加入对参数的控制，即在模型损失基础上加上参数值控制。也可以理解为将参数的先验知识加入到模型中，防止模型过拟合。先验知识的作用举例如下：

如抛硬币的时候如果只能抛5次，很可能5次全正面朝上，这样你就得出错误的结论：正面朝上的概率是1，此时就会产生过拟合。但如果此时在模型里加正面朝上概率是0.5的先验，结果就不会那么离谱，这其实就是正则。

从例子中可以得出，当不加入正则化的时候，模型为了拟合所有的训练数据，\(w\)可以变得任意大，此时模型的方差会非常大。而加入参数的先验知识后，模型就会变得更加稳定，此时的模型方差会变小。加入正则化是在bias和variance之间做一个tradeoff。

加入正则化后的损失函数可以表示为：

\[Loss_{new}=\frac{1}{2}\underset{n=1}{\overset N \sum}(y_n-w^T\phi(x_n))^2+\frac{\lambda}{2} \underset{j=1}{\overset D\sum}(w_j)^q \]

不同的q值对应的正则化项的轮廓线


其中:

\(q=1\)时对应的为\(L_1\)正则项，加入\(L_1\)正则项的线性回归被成为Lasso（拉锁）回归

\(q=2\)时对应的为\(L2\)正则项，加入\(L_2\)正则项的线性回归被称为Ridge（岭）回归

2、逻辑回归

 线性回归一般用于解决回归问题，那对于分类问题该如何解决呢？根据公式(3)可知，回归问题的输出可以为任意值，而分类问题的输出是固定值，如二分类的输出为\(\{0,1\}\)，因此需要将线性回归的输出转换为0或1的值。最直接的处理方法是使用阶跃函数：

\[t = \begin{cases} 0 & x<0 \\ 1 & x \ge 1\end{cases} \tag{6} \]

单位阶跃函数和sigmoid函数

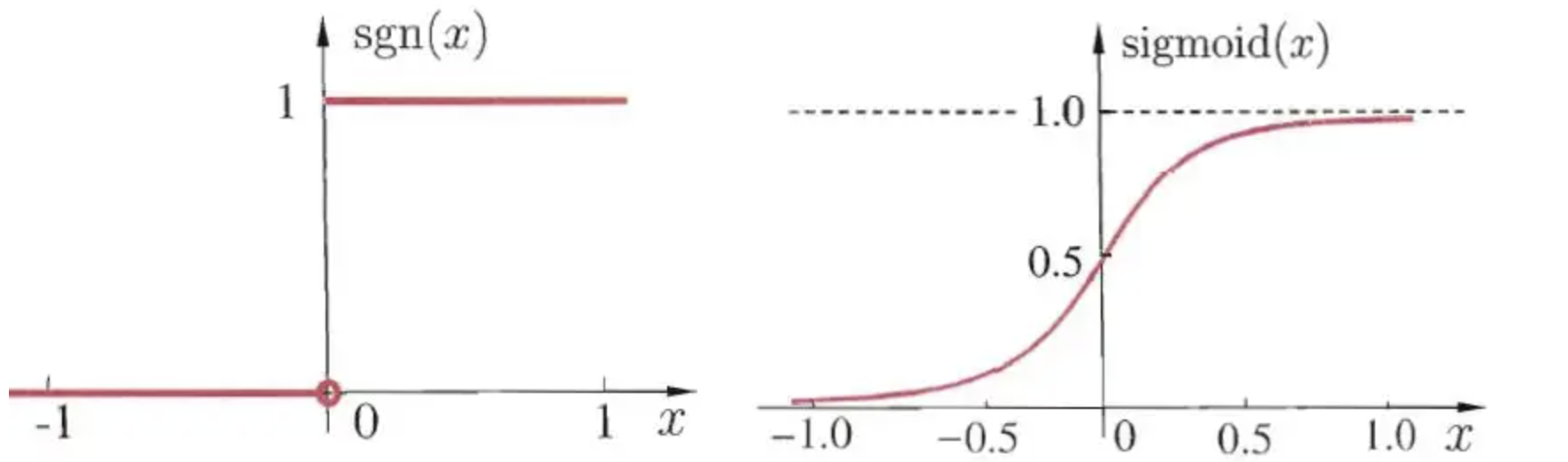
但是单位阶跃函数不连续，无法通过计算导数的方式对参数进行优化。于是需要找一个在一定程度上近似单位阶跃函数的“替代函数”，并希望它单调可微。而Sigmoid函数正是这样一个常用的替代函数。Sigmoid函数将\(x\)的值转化为一个接近0或1的\(y\)值，并且其输出值在\(x=0\)的附近变化很陡。Sigmoid函数可以表示为：

\[y = \frac{1}{1 + exp(-x)} \tag{7} \]

 此时对应模型的输出可以表示:

\[y = sigmoid(x)=\frac{1}{1 + exp(-z)} \tag{8} \]

其中，\(z=\sum_{i=0}^Dw_ix_i\)

 从图中可以经过sigmoid函数转换后的值，实际上也可以表示为预测为1的概率值，从而通常可以将经过sigmoid转换后的公式表示为概率形式，即

\[P(Y=1|x)=\frac{1}{1+exp(-z)}=\frac{\sum_{i=0}^Dexp(w_i^Tx_i)}{1+\sum_{i=0}^Dexp(w_i^Tx_i)} \tag{9} \]

且

\[P(Y=0|x)=1- P(Y=1|x)=\frac{1}{1+\sum_{i=0}^Dexp(w_i^Tx)} \tag{10} \]

2.1 模型参数估计

 由于Logistic的输出值只有\(\{0,1\}\)两个取值，很自然的可以假设其服从伯努利分布，即

\[Bern(x|\mu)=\mu^x(1-\mu)^{1-x} \tag{11} \]

假设有\(N\)个样本，采用伯努利分布和极大似然估计法，可得：

\[\begin{align} p({\tt y}|X,w) & =\underset{n=1}{\overset N \prod}[p(y=1|x_i)]^{y_i}[p(y=0|x_i)]^{1-y_i} \\ & = \underset{n=1}{\overset N \prod}[p(y=1|x_i)]^{y_i}[1- p(y=1|x_i)]^{1-y_i} \tag{12} \end{align} \]

其中\(P(y=1|x_i)=\frac{exp(w^Tx_i)}{1+exp(w^Tx_i)}\)​，从而可得：

\[\begin{align} \ln p(w|y,x) & =\underset{n=1}{\overset N \sum}[y_i \log p(y=1|x_i) + (1-y_i) \log (1-p(y=1|x_i))] \\ & = \underset{n=1}{\overset N \sum}[y_i \log \frac{p(y=1|x_i)}{1-p(y=1|x_i)}+ \log (1-p(y=1|x_i))] \\ & = \underset{n=1}{\overset N \sum}[y_i (w^Tx_i) - \log (1+exp(w^Tx_i))]\end{align} \tag{13} \]

利用优化算法（如梯度下降或牛顿法​），可以得到\(w\)的估计值，记为\(w_{ML}\)，优化方法可以参考：https://www.cnblogs.com/laojifuli/p/15046910.html。

2.2 两组等价概念

  在罗辑回归文献中，经常会遇到Logistic分布和Sigmoid函数、交叉熵损失和似然函数，下面简单记录一下这两组名称之间的关系。

2.2.1 Logistic分布与Sigmoid函数

  设\(X\)时连续变量，\(X\)服从Logistic分布是指\(X\)具有下列分布函数：

\[F(X) = P(X\leq x)=\frac{1}{1+exp(-\frac{x-\mu}{\gamma})} \tag{14} \]

从公式(7)可以得到Sigmoid函数为\(y = \frac{1}{1 + exp(-x)}\)
通过观察可以得到，Sigmoid函数与均值\(\mu=0\)，方差\(\sigma=1\)的Logistic分布函数是等价的。

2.2.2 交叉熵损失函数和极大似然函数

  设有一组训练样本\(X=\{x_1,x_2,...,x_m\}\)，该样本的分布为\(p(x)\)，假设使用\(\theta\)参数化模型得到\(q(x;\theta)\)，现用这个模型来估计\(X\)的概率分布，得到似然函数

极大似然估计：事件件发生概率最大的参数值，作为总体参数的估计值

\[(\theta) = q(X;\theta) = \underset{i}{\overset m \prod} q(x_i;\theta) \tag{15} \]

最大化似然估计就是求得\(\theta\)是的\(L(\theta)\)的值最大，也就是:

\[\theta_{ML}=\underset{\theta}{argmax}\underset{i}{\overset m \prod} q(x_i;\theta) \propto \underset{\theta}{argmax} \frac{1}{m}\underset{i}{\overset m \sum}\log q(x_i;\theta) \rightarrow \underset{\theta}{argmax} E_{x \sim P}\underset{i} {\overset m \sum }\log q(x;\theta) \tag{16} \]

等式两边分别取log，且等式左边取\(\log(\theta)\)和\(\theta\)的趋势是一致的。\(\frac{1}{m}\underset{i}{\overset m \sum}\log q(x_i;\theta)\)相当于求随机变量\(X\)的函数\(\log(X;\theta)\)的均值，根据大数定律，随着样本容量的增加，样本的算数平均值将趋于随机变量的期望，也就是说\(\frac{1}{m}\underset{i}{\overset m \sum}\log q(x_i;\theta) \rightarrow E_{x\sim P}(\log q(x;\theta))\)

交叉熵：实际输出（概率）与期望输出（概率）的距离。可以表示为：

\[H(p,q)=-\sum_{i=1}^n p(x_i)lopq(x_i) = E_{x\sim P}(-\log q(x)) \tag{17} \]

从而可以得到：当样本量较大的时候，似然函数与交叉熵函数的表达是一致的，因此极大似然函数与极大交叉熵函数也是等价的。

\(P(Y=0|x)=\frac{1}{1+exp(w_{ML}^Tx)}\)

3 多项逻辑回归

二元变量只能取两种可能值中的某一种，多元变量是有多个取值，如\(K=6\)​​​种取值的分布\(y=(0,0,1,0,0,0)\)​​​，此时对应\(y_3=1\)​​​

使用\(\mu_k\)​​​表示\(y_k=1\)​​​的概率，那么\(x\)​​​的分布就是

\[p(y|\mu)=\underset{k=1}{\overset K \prod}\mu_k^{t_k} \tag{18}​ \]

其中\(\mu=(\mu_1,...,\mu_K)^T\)​，参数\(\mu_k\)​要满足\(\mu_k>0\)​和\(\underset{t}\sum p(y|\mu)= \underset{k=1}{\overset K \sum}\mu_k=1\)​​​

并且

\[{\Bbb E}[y|\mu]=-\underset{y}\sum p(y|\mu)y= (\mu_1,...,\mu_K)^T=\mu \tag{19} \]

此时对应的多项逻辑回归模型是：

\[P(Y=k|x)=\frac{exp(w_k^Tx)}{1+\sum_{i=1}^{K-1} exp(w_i^Tx)},\ k=1,2,...,K-1 \tag{20} \]

\[P(Y=K|x)=\frac{1}{1+\sum_{i=1}^{K-1} exp(w_i^Tx)} \tag{21} \]

Logistic回归的参数估计方法也可以推广到多项Logistic回归

4. 参考文献

link function：https://www.zhihu.com/question/28469421
指数分布族：https://blog.csdn.net/Queen0911/article/details/103378732
交叉熵损失函数：https://blog.csdn.net/weixin_41806692/article/details/82463577
Logistic损失函数：https://blog.csdn.net/u013385018/article/details/92644918
1）均方误差损失函数不是凸函数
2）会出现梯度消失
交叉熵和极大似然函数的关系：https://www.cnblogs.com/breezezz/p/11277131.html
为什么使用对数损失函数：https://blog.csdn.net/saltriver/article/details/63683092
https://blog.csdn.net/saltriver/article/details/53364037