动态规划之理论分析
大家好,经过前两篇的分析,相信大家对动态规划都有了一定的认识,也能感受到动态规划强大的算法思想。今天我们就来总结一下动态规划能解决哪些问题,以及解决动态规划问题的思考过程是怎么样的?我们一起出发吧。
一、问题模型
动态规划一般是用来解决最优解。而在解决的过程中是需要经历多个阶段的决策。每个阶段都会对应一组状态。我们需要找到一组决策,经过这些决策后,能求出问题的最优解。我们这类问题抽象成“多阶段决策最优模型”。
动态规划还有三大特征,分别是最优子结构、无后效性和重复子问题,只有当原问题满足这三大特征时,我们才能使用动态规划的算法思想来解决。下面我们来分别看一下这三个特征。
1.最优子结构
最优子结构规定了原问题和子问题的关系。原问题的最优解包含子问题的最优解。反过来说,我们可以通过子问题的最优解来求出原问题的最优解。
2.无后效性
(1)无后效性是指在推导后面阶段状态的时候,只依赖于前面阶段的的状态,而不会去关心这个状态是怎么一步步得来的。比如斐波那契数列F(5)=F(4)+F(3),则可以看出F(5)只依赖于F(4)和F(3)这两个状态的值,而不用管他们是如何得来的。
(2)一旦某个状态确定了,就不受之后阶段的决策影响。
3.重复子问题
就是原问题经过拆分成多个子问题时,子问题和子问题之间存在重复计算的情况。
下面我们来结合实例,来比较透彻的了解一下上面的理论部分。
问题描述:我们假设有一个n*n的矩阵w[n][n](矩阵中存储正整数)。棋子从矩阵的左上角开始移动到矩阵的右下角。棋子每次只能向下或者向右移动一步。棋子可以有很多不同的路径走完这个矩 阵。我们把每条路径经过的数字相加作为路径长度,那最短的路径长度是多少呢?
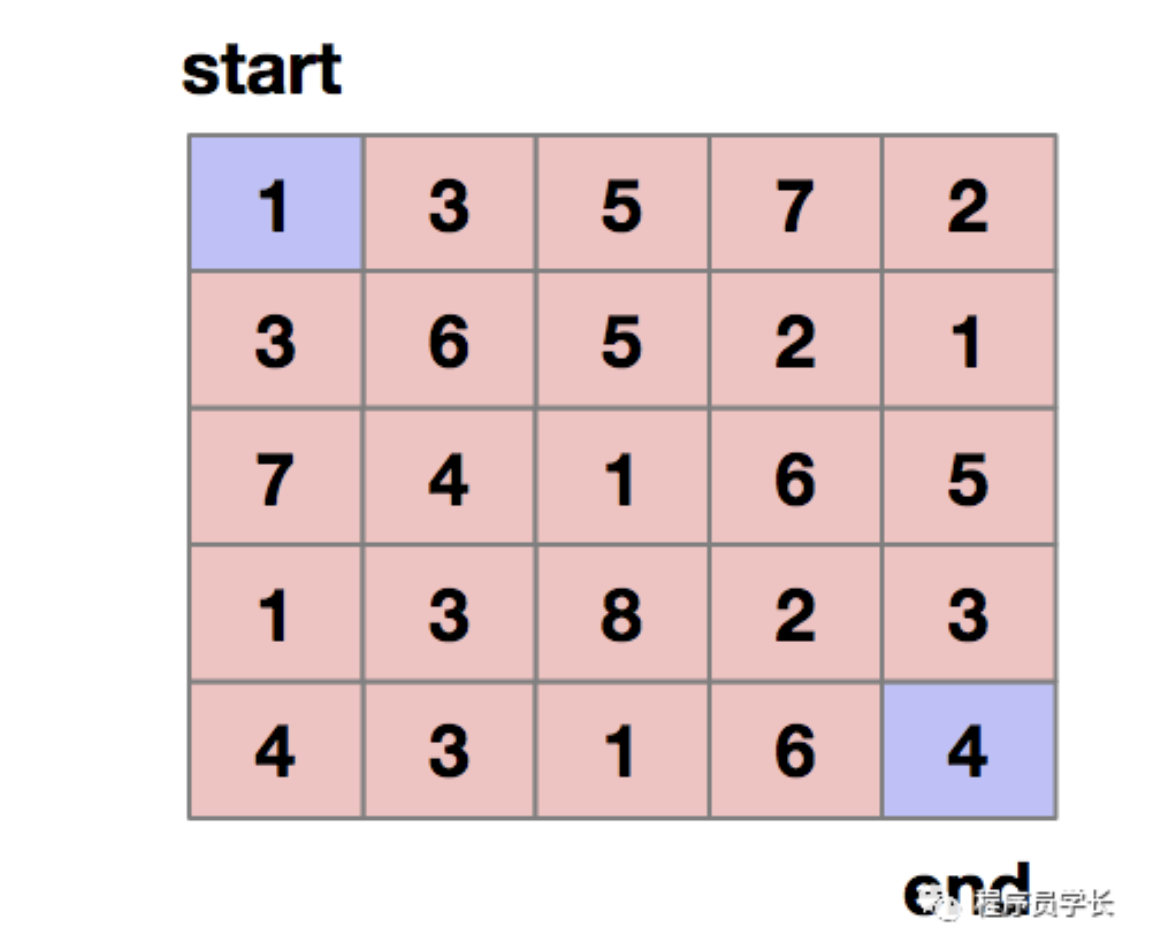
我们从start开始走,一直走到end位置,一共需要走2*(n-1)步,也就对应这2*(n-1)个阶段,每个阶段都有向下走还是向右走两种决策,不同的决策对应着不同的状态。所以这符合多阶段决策,而最后求解的是最短路径长度,所以符合动态规划的问题模型。
接下来我们看它是否符合动态规划的三个特征呢?如下所示,从(0,0)位置走到(1,1)位置有两种走法,所以符合重复子问题。
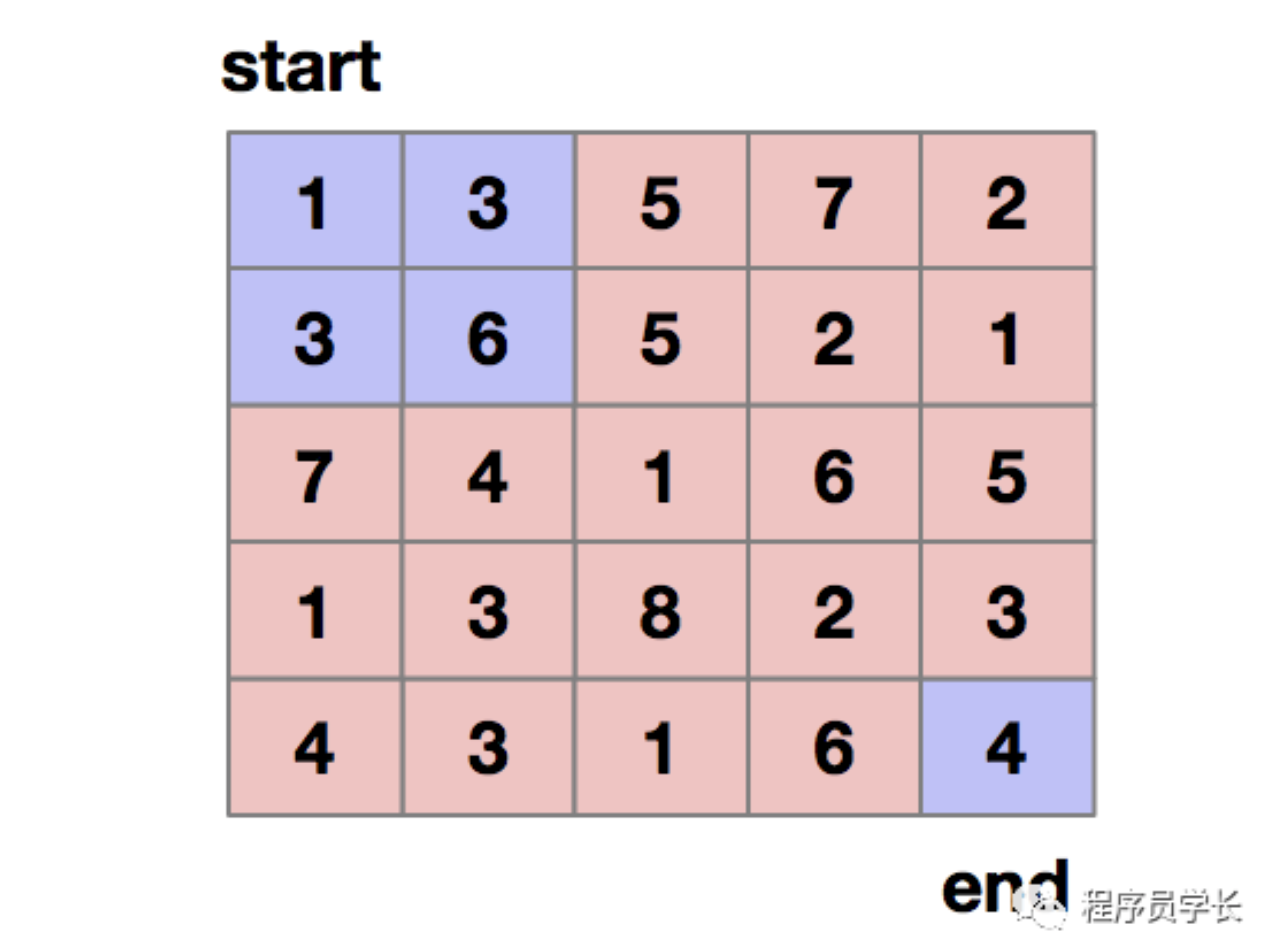
下面我们再了看一下无后效性这个特征。我们要想走到(i,j)这个位置,我们只能通过(i-1,j)和(i,j-1)这两个位置移动过来,也就是说,我们只需要关心(i-1,j)和(i,j-1)这两个位置的状态,而不必关系是如何从(0,0)位置走到这个位置的。而且,我们这里只允许向下或者向右走,不允许后退,所以前面阶段的状态确定之后,就不会被后面阶段的决策所改变。所以这个问题是符合“无后效性”这个特征的。
我们把从(0,0)位置走到(i,j)位置的最短路径记为为min(i,j),因为我们只能向右或者向后移动,所以我们只能从(i-1,j)和(i,j-1)两个位置到达(i,j)。换句话说,就是min(i,j)只能通过min(i-1,j)和min(i,j-1)两个状态推导出来。所以这个问题就符合“最优子结构”。
min(i,j)=w[i][j]+min(min(i-1,j),min(i,j-1))
所以这个问题是符合动态规划问题模型的,所以我们可以采用动态规划思想来解决这个问题。
二、解决思路
解决动态规划问题,一般有状态转移表法和状态转移方程法这两种方法。
1.状态转移表法:
我们先定义一个状态表,一般状态表都是二维的。我们根据决策的先后顺序,从前往后,根据递归关系,分阶段的填充状态表中的每个状态。最后,我们把递归填表的过程翻译成代码就完成了。我们接下来看如何用状态转移表法来求最短路径这个问题的。我们画出一个二维数组,表中的行、列表示棋子所在的位置,表中的数值表示从起点到这个位置的最短路径。然后,我们按照决策过程依次去填表,前两步的走法如下图所示:
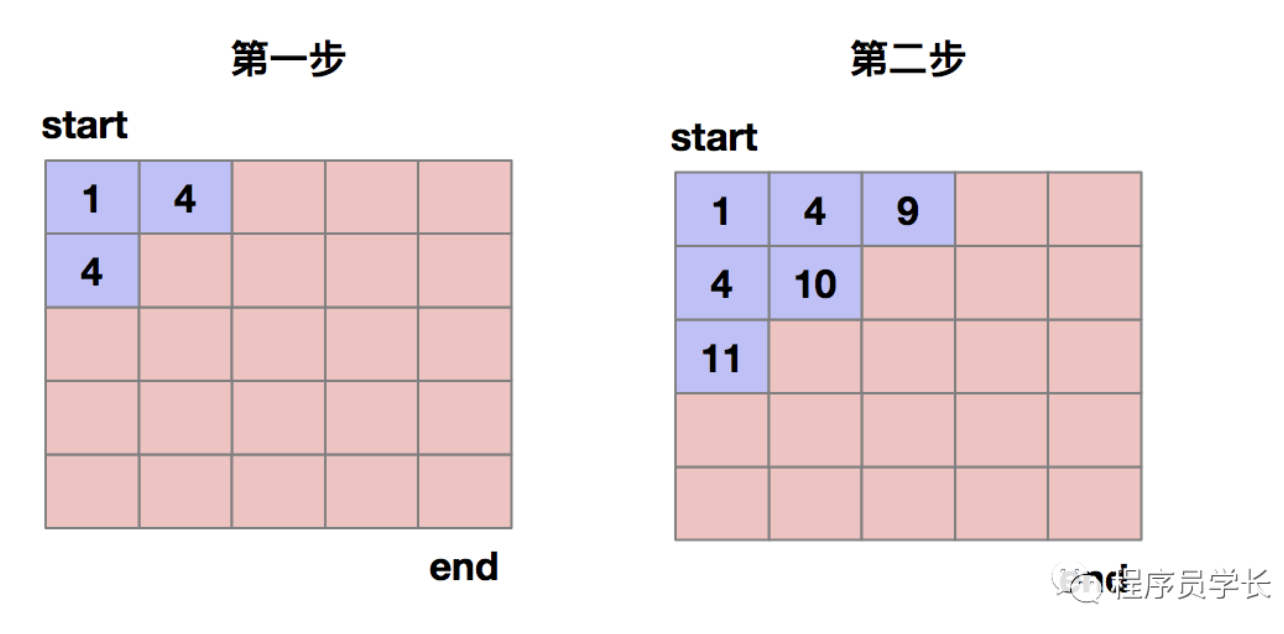
我们来看一下代码如何实现。
def minDis(data,n):
status=[[0 for _ in range(n)] for _ in range(n)]
sum=0
#第一行赋值
for i in range(n):
sum=sum+data[0][i]
status[0][i]=sum
#第一列赋值
sum=0
for i in range(n):
sum=sum+data[i][0]
status[i][0]=sum
for i in range(1,n):
for j in range(1,n):
status[i][j]=data[i][j]+min(status[i-1][j],status[i][j-1])
return status[n-1][n-1]
data=[[1,3,5,7,2],
[3,6,5,2,1],
[7,4,1,6,5],
[1,3,8,2,3],
[4,3,1,6,4]]
n=5
print(minDis(data,n))
2.状态转移方程法
状态转移方程法和递归的解题思路类似。我们根据最优子结构,写出递推公式,也就是所谓的状态转移方程。然后根据状态转移方程,实现代码就好了。这里一般有两种实现方法,一种是递归加备忘录方法,另一种是迭代递推。
我们看这个最短路径的例子,它的状态转移方程如下所示:
min(i,j)=w[i][j]+min(min(i-1,j),min(i,j-1))
我们这里采用递归加备忘录方法来实现,另一种迭代递推的实现和状态转移表法的代码实现是一致的,只是思路不同而已。
import sys
data=[[1,3,5,7,2],
[3,6,5,2,1],
[7,4,1,6,5],
[1,3,8,2,3],
[4,3,1,6,4]]
n=5
mem=[[0 for _ in range(5)] for _ in range(5)]
def minDis(i,j):
if i==0 and j==0:
return data[0][0]
if mem[i][j]>0:
return mem[i][j]
minLeft = sys.maxsize
if j-1>=0:
minLeft=minDis(i,j-1)
minUp = sys.maxsize
if i-1>=0:
minUp=minDis(i-1,j)
current=data[i][j]+min(minLeft,minUp)
mem[i][j]=current
return current
print(minDis(n-1,n-1))
到这里为止,我们的动态规划就聊完了。希望你已经对动态规划算法思想有所掌握。如果没有明白也没关系,多做几道题,然后回过头来再看,一定会有收获的。
更多硬核知识,请关注公众号。



