排序算法你学会了吗?
排序对于大家来说肯定都不陌生,我们在平常的项目里都会或多或少的用到排序功能。排序算法作为一个最基础最常用的算法,你真的学会了吗?下面我来带领大家由浅入深的学习一下经典的排序算法。
如何分析一个排序算法
学习排序算法,我们不仅要学习它的算法原理、代码实现,更要学会如何评价、分析一个排序算法。分析一个排序算法,主要是从以下3个方面入手。
-
排序算法的执行效率
我们在分析排序算法的时间复杂度时候,要分别给出最好情况、最坏情况和平均情况下的时间复杂度。除此之外,我们还要了解最好、最坏时间复杂度对应的要排序的原始数据是什么样子。
-
排序算法的内存消耗
算法的内存消耗可以通过空间复杂度来衡量,不过对于排序算法来说,引入了“原地排序”这个概念,原地排序算法,就是指空间复杂度是O(1)的排序算法。
-
排序算法的稳定性
排序算法的稳定性是指,如果待排序的序列中存在值相等的元素,经过排序
之后,相等元素之间原有的先后顺序不变。
经典的排序算法
一、冒泡排序
我们先从最简单的冒泡排序开始,学习我们的经典排序算法。
冒泡排序的算法原理是:依次比较相邻的俩个元素,看是否满足大小关系要求,如果不满足就让他俩互换。一次冒泡操作会让至少一个元素移动到它应该在的位置,就这样重复n次,这完成了n个数据的排序工作。
下面我们来看一个例子,假如我们要对5,7,8,3,1进行从小到大排序。第一次冒泡操作的过程如下:
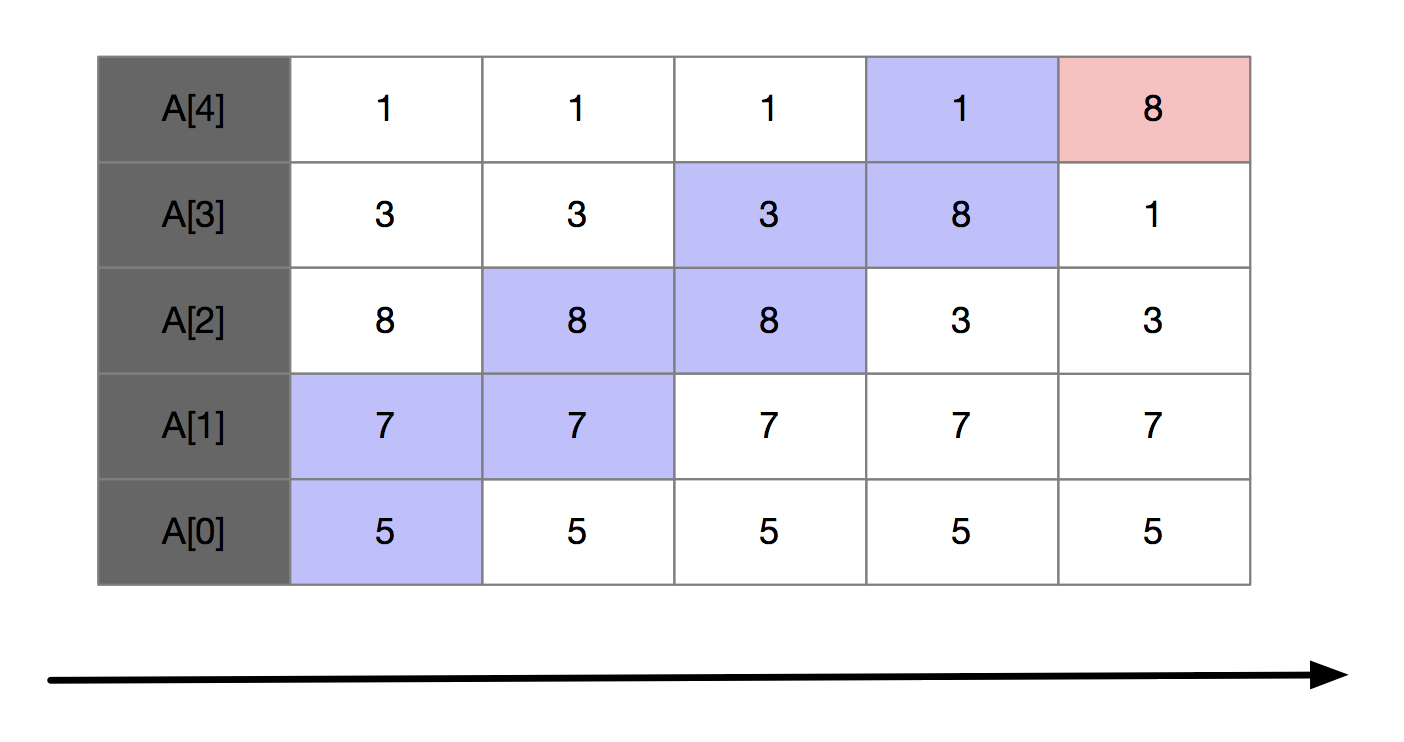
可以看出,经过一次冒泡排序之后,8已经存储在正确的位置上了。所以,只要经过5次冒泡操作,就可以完成数据的排序了。

冒泡排序算法原理比较容易理解,我们来看一下它的代码实现。
def bubble_sort(a,n):
if n<=1:
return
##提前退出标志位
flag=False
for i in range(n):
for j in range(n - i - 1):
if (a[j] > a[j + 1]):
temp = a[j]
a[j] = a[j + 1]
a[j + 1] = temp
flag=True
if(not flag):
break
a=[5,7,8,3,1]
bubble_sort(a,len(a))
print(a)
接下来我们来分析一下冒泡排序。
-
冒泡排序是原地排序算法吗?
冒泡的过程只是涉及相邻数据的交换操作,只需要常量级的临时空间,所以他的空间复杂度是O(1),是一个原地排序算法。
-
冒泡排序是稳定的排序算法吗?
当有相邻的两个元素大小相同时,我们不做数据交换,所以相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。
-
冒泡排序的时间复杂度是多少?
最好的情况下,要排序的数据已经是有序的,我们只需要进行一次冒泡操作,所以最好的时间复杂度是O(1)。最坏的情况下,要排序的数据是逆序的,我们需要进行n次冒泡操作,所以最坏情况时间复杂度是O(n2)
二、插入排序
我们将数组中的数据分为两个区间,已排序区间和未排序区间。插入算法的核心思想就是取未排序区间中的元素,在已排序的的区间中找到合适的位置将其插入进去,并保证已排序区间数据一直是有序的。重复此过程,直到未排序区间为空。 如图,要排序的数据序列为5,7,8,3,1,其中左侧为已排序区间,右侧是未排序区间。
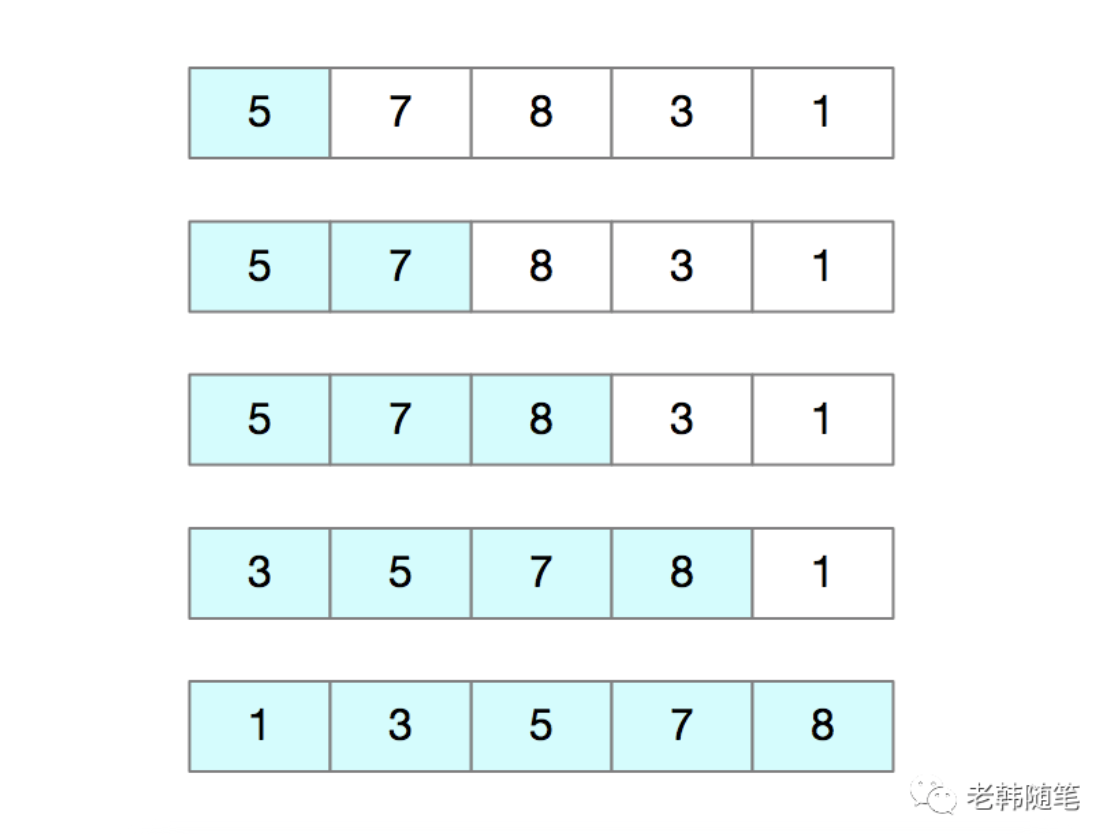
我们来看一下他的代码实现。
def insert_sort(a,n):
if n<=1:
return
for i in range(1,n):
value=a[i]
j=i-1
while(j>=0):
if(a[j]>value):
a[j+1]=a[j]
j=j-1
else:
break
a[j+1]=value
a=[5,7,8,3,1]
insert_sort(a,len(a))
print(a)
接下来我们来分析一下插入排序算法。
-
插入排序算法是原地排序吗?
从上面的代码来看,插入排序算法不需要额外的存储空间,所以空间复杂度为O(1),也就是说这是一个原地排序算法。
-
插入排序是稳定的排序算法吗?
在插入排序中,我们可以将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法。
-
插入排序的时间复杂度是多少?
如果待排序的数据是有序的。我们每次只比较一个数据就能确定插入位置,所以最好的时间复杂度是O(n)。如果待排序的数据是逆序的,每次插入都相当于在数组的首部插入数据,所以需要移动大量的数据,所以最坏的情况,时间复杂度是O(n*n)。
三、选择排序
选择排序类似于插入排序,也分为已排序区和未排序区。但是选择排序每次都会从未排序区间找到最小的元素,将其放入已排序区间的末尾。如下图所示:
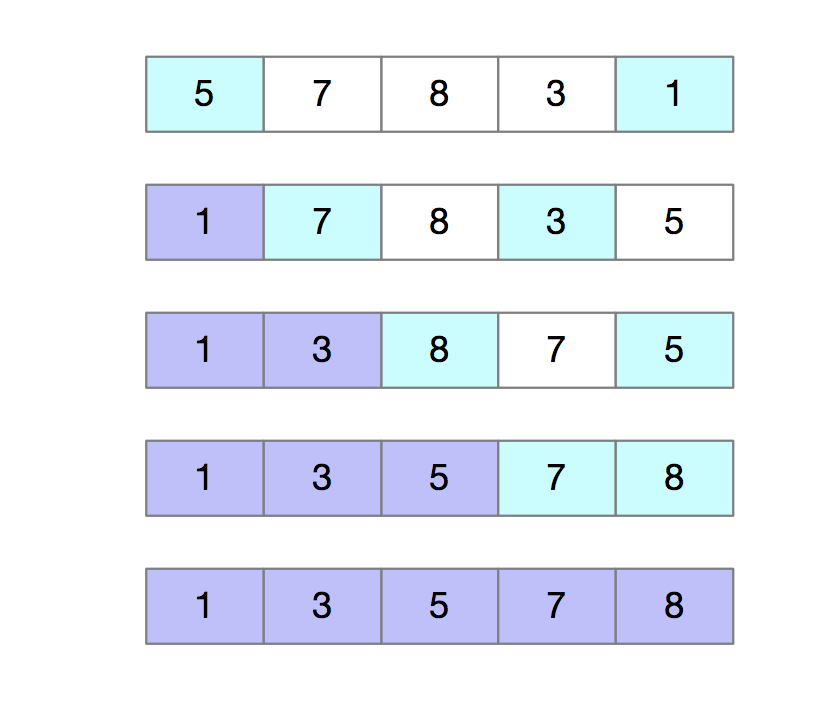
def select_sort(a,n):
if n<=1:
return
for i in range(n):
min_index=i
for j in range(i,n):
if a[j]<a[min_index]:
min_index=j
temp = a[i]
a[i] = a[min_index]
a[min_index] = temp
a=[5,7,8,3,1]
insert_sort(a,len(a))
print(a)
下面我们来分析一下选择排序。
-
选择排序算法是原地排序吗?
通过代码可以看到,选择排序只用到了常数级的临时空间,所以选择排序的空间复杂度为O(1),是一种原地排序算法。
-
选择排序的时间复杂度是多少?
通过代码可以看到,选择排序的最好情况的时间复杂度、最坏情况的时间复杂度和平均情况的时间复杂度都是O(n*n)。
-
选择排序是稳定的排序算法吗?
选择排序是不稳定的排序算法。从代码可以看到,选择排序每次都找剩余未排序元素中的最小值来和前面的元素交换位置,这样就破坏了稳定性。
四、归并排序
归并排序的思想是:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好的两部分合并在一起,这样整个数组就有序了。
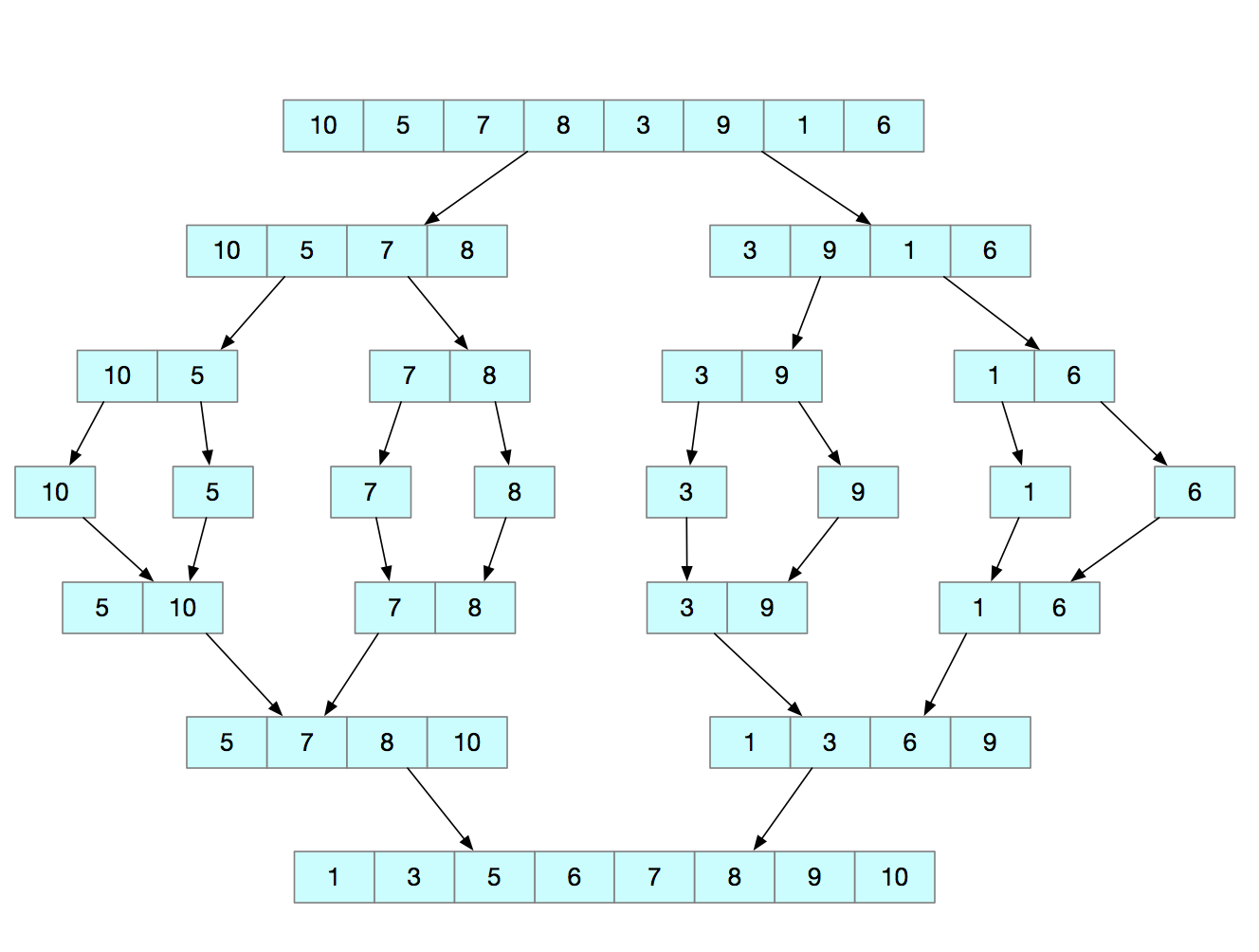
归并排序使用的是分治思想。分治就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大的问题也就解决了。
def merget_sort(A,n):
merget_sort_m(A,0,n-1)
def merget_sort_m(A,p,r):
#递归终止条件
if p>=r:
return
q=p+(r-p)//2
merget_sort_m(A,p,q)
merget_sort_m(A,q+1,r)
#将A[p:q],A[q+1:r]合并到A[p:r]
merge(A,p,q,r)
def merge(A,p,q,r):
i=p
j=q+1
tmp=[]
while i<=q and j<=r:
if A[i]<=A[j]:
tmp.append(A[i])
i=i+1
else:
tmp.append(A[j])
j = j + 1
start=i if i<=q else j
end=q if i<=q else r
tmp.extend(a[start:end+1])
a[p:r+1]=tmp
a=[4, 3, 2, 1]
merget_sort(a,len(a))
print(a)
下面我们来分析一下归并排序。
-
归并排序是稳定的排序算法吗?
结合代码可以看出,归并排序稳定不稳定的关键在于merge函数,在合并的过程中,如果A[p:q]和A[q+1:r]之间值有相同的元素时,把A[p:q]中的元素放入tmp数组中,这样就保证了值相同的元素在合并前后顺序不变。所以归并排序是一个稳定的排序算法。
-
归并排序的时间复杂度是多少?
归并排序的时间复杂度是O(nlogn)
-
归并排序的空间复杂度是多少?
通过代码可以看到,归并排序不是原地排序算法,需要借助额外的存储空间。通过merge函数可以看到,归并排序的空间复杂度是O(n)。
五、快速排序
最后,我们来看一下快速排序。快速排序也是利用分治的思想。快速排序的核心思想是:如果要排序数组中下标从p到r之间的数,我们选择p到r之间的任何一个数作为pivot(分区点)。我们遍历p到r之间的数,将小于pivot的放到左边,将大于pivot的放到右边,将pivot放到中间。经过这一步后,数组p到r之间的数据就被分成了三部分,前面p到q-1都是小于pivot的,中间是pivot,后面q+1到r都是大于pivot的。
假如我们选择数组p到r的最后一个元素作为pivot,对数组5,7,8,3,6来进行快速排序。我们来看一下代码实现。
def quick_sort(A,n):
quick_sort_m(A,0,n-1)
def quick_sort_m(A,p,r):
#递归终止条件
if p>=r:
return
q=partition(A,p,r)
quick_sort_m(A,p,q-1)
#将A[p:q],A[q+1:r]合并到A[p:r]
quick_sort_m(A,q+1,r)
def partition(A,p,r):
povit=A[r]
i=p
for j in range(p,r):
print(j)
if(A[j]<povit):
temp=A[i]
A[i]=A[j]
A[j]=temp
i=i+1
temp=A[i]
A[i]=A[r]
A[r]=temp
return i
a=[5, 7, 8, 3, 6]
quick_sort(a,len(a))
print(a)
其中partition函数是选择数组的最后一个元素作为pivot,然后对A[p:r]分区,函数返回pivot的下标。
我们来看一下一次快速排序的过程。如下图所示:
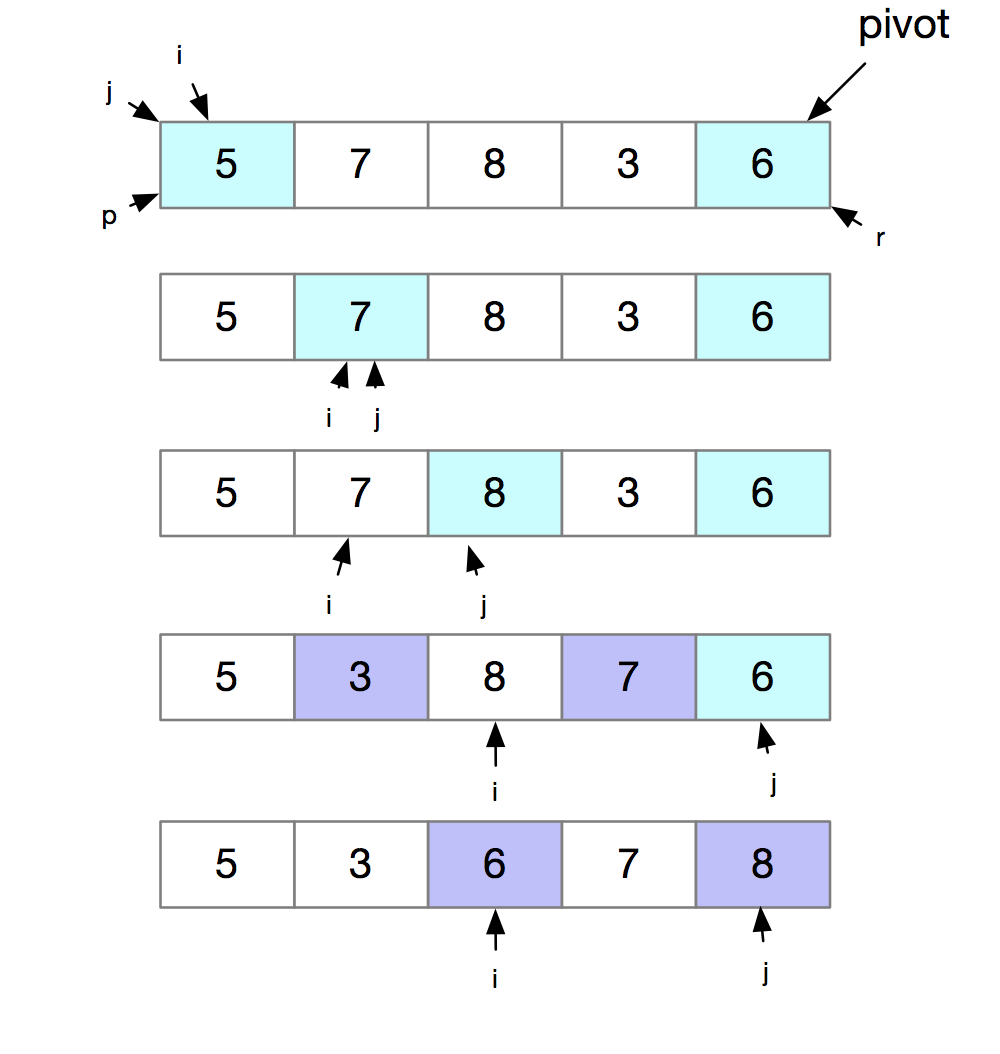
下面我们来分析一下快速排序。
-
快速排序是稳定的排序算法吗?
因为分区会涉及到交换操作,如果数组中有两个相同的元素,经过分区操作以后,相同元素的先后顺序会发生改变,所以快速排序不是稳定的排序算法。
-
快速排序算法的时间复杂度是多少?
快速排序也是用递归来实现的,如果每次分区操作,正好把数组分成大小相
近的两个小区间,那快排的时间复杂度就是O(nlogn)。最坏的情况是如果数组是有序的,每次取最后一个元素作为pivot,那每次分区得到的区间是不均等的。我们需要n次分区操作,才能完成快排的整个过程。每次分区大概都需要扫描n/2个元素。这种情况下,快排的时间复杂度就从O(nlogn)退化成O(n*n)。
-
快速排序算法的空间复杂度是多少?
通过代码可以看到,快速排序只用到了常数级的临时空间,所以选择排序的
空间复杂度为O(1),是一种原地排序算法。
到此为止,我们已经分享了五种经典的排序算法,你学会了吗?
欢迎大家留言和我交流。
了解更多有趣内容,获取更多资料,请关注公众号“程序员学长” 。



