数据结构与算法复习--（2）

算法和算法分析

• 算法的定义
  • 对特定问题求解方法和步骤的一种描述，它是指令的有限序列。其中每个指令表示一个或多个操作。
• 算法的描述
  • 自然语言：英语、中文
  • 流程图：传统流程图、NS流程图
  • 伪代码：类语言：类C语言
  • 程序代码：C语言程序、Java语言程序
• 算法与程序
  • 算法是解决问题的一种方法或一个过程，考虑如何将输入转换成输出，一个问题可以电多种算法
  • 程序是用某种程序设计语言对算法的具体实现。
    
• 算法特性：一个算法必须具备以下五个重要特性
  • 有穷性 一个算法必须总是在执行有穷步之后结束，且每一步都在有穷时间内完成。
  • 确定性 算法中的每一条指令必须有确切的含义，没有二义性，在任何条件下，只有唯一的一条执行路径，即对于相同的输入只能得到相同的输出。
  • 可行性 算法是可执行的，算法描述的操作可以通过已经实现的基本操作执行有限次来实现。
  • 输入 一个算法有零个或多个输入。
  • 输出 一个算法有一个或多个输出。
• 算法设计的要求
  • 正确性(Correctness)
  • 可读性(Readability)
  • 健壮性(Robustness)
  • 高效性(Efficiency)

一个好的算法在满足设计要求的前提下，主要考虑算法的效率，通过算法的效率高低来评判不同算法的优劣程度

• 算法效率一下两个方面来考虑：
  1.时间效率：指的是算法所耗费的时间
  2.空间效率：指的是算法执行过程中所耗费的存储空间

  • 时间效率和空间效率有时候是矛盾的

• 算法时间效率的度量

  • 算法时间效率可以用依据该算法编制的程序在计算机上执行所消耗的时间来度量
  • 两种度量方法
    • 事后统计
      • 将算法实现，测算其时间和空间开销
    • 事前分析
      • 对算法所消耗资源的一种估算方法
      • 一个算法的运行时间是指一个算法在计算机上运行所耗费的时间大致可以等于计算机执行一种简单的操作(如赋值、比较、移动等）所需的时间与算法中进行的简单操作次数乘积。
        算法运行时间=一个简单操作所需的时间*简单操作次数
      • 也即算法中每条语句的执行时间之和
        算法运行时间=Σ每条语句的执行次数*该语句执行一次所需的时间

• 为了便于比较不同算法的时间效率，我们仅比较它们的数量级
  例如：两个不同的算法，时间消耗分别是：
  T1(n)=10n^2 与 T2(n)=5n^3

• 若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度(O是数量级的符号)，简称时间复杂度。
  例：T(n)=2n³⁺³ⁿ2+2n+1
  n➡∞时，T(n)/n^{3➡2，这表示n充分大时，T(n)与n}3是同阶或同数量，引入“O”记号，则T(n)可记作：
  T(n)=O(n^3)
  

• 对于复杂的算法，可以将它分成几个容易估算的部分，然后利用大O加法法则和乘法法则，计算算法的时间复杂度：
  a> 加法规则
  

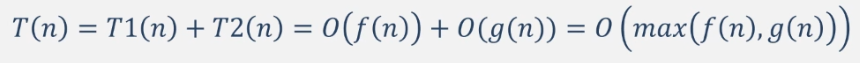
  b> 乘法规则
  

时间复杂度T(n)按数量级递增顺序为：

空间复杂度

• 算法要占据的空间

  • 算法本身要占据的空间，输入/输出，指令，常数，变量等
  • 算法要使用的辅助空间