医疗花费预测(保姆级教程)
目标
想要一开始快速抓住一个实验的方向,我觉得一个好方法就是抓住实验目的。
本实验:根据一个人的年龄、性别、BMI、子女个数、是否吸烟和生活地区,预测这个人在医疗方面花费的金额。
线性回归
这里我想问个问题,线性回归是什么,或者说针对于DBSCAN聚类算法之后得到的样本,进行线性回归的作用?
线性回归是一种统计分析方法,用于通过一个或多个自变量(特征值)和因变量(目标值)之间的线性关系进行建模
针对本实验:DBSCAN聚类算法可以将数据集划分为不同的簇,线性回归操作为每个簇建立一个特定的线性关系模型,从而更准确地分析和预测每个簇内的数据点。
追根溯源的了解
因为我们小组负责的是三部分:线性回归、结果预测、结果分析。
经过上述的解释,我们会发现,要想实现准确的线性回归、相对合理的结果分析,其实需要从头全方位,做完成前面所有的步骤,包括:数据读取、预处理、分析。
数据读取
import pandas as pd train = pd.read_csv("E:/《数据分析与可视化》/第6章 医疗花费预测/train.csv") train.head(5)
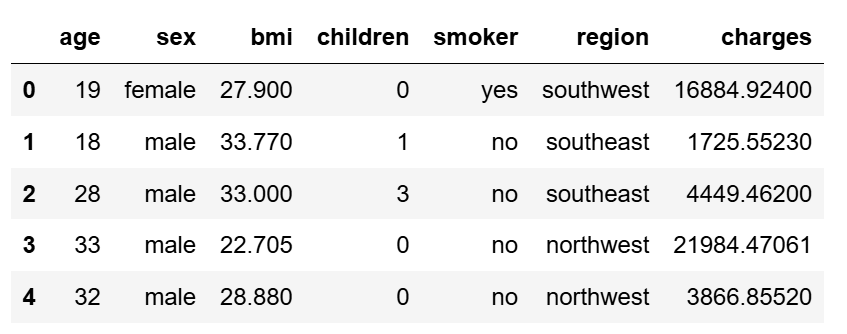
数据预处理
from sklearn.preprocessing import OrdinalEncoder import numpy as np encoder = OrdinalEncoder(dtype=np.int) train[['sex', 'smoker', 'region']] = \ encoder.fit_transform(train[['sex', 'smoker', 'region']]) train.head(5)
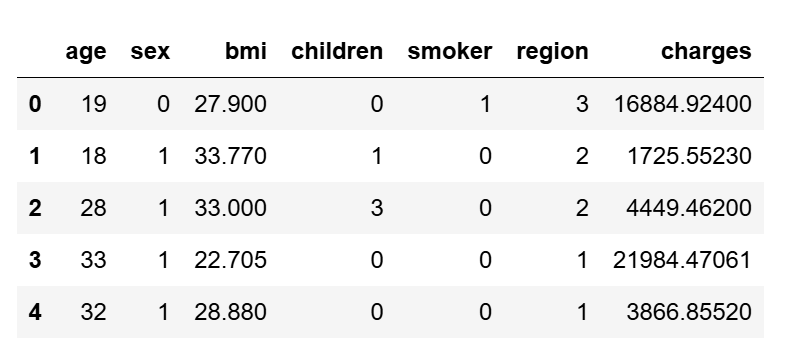
查看数据分布
在处理完字符串类型的转换后,对其余数据进行观察,发现age、bmi和charges属于连续数据,而children是离散数据。
这边老师说过:离散数据是整数等只能取特定值的数据
这边我从导数(瞬时变化率)方面来解释一下:
离散数据:不能直接求导,相邻点的之间只能用差分来求解瞬时变化率
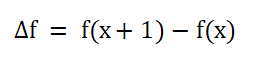
连续数据:能直接求导,用导数来表示瞬时变化率
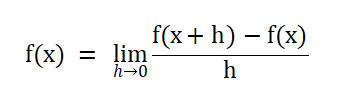
在本案例中,使用seaborn库对连续数据的分布进行可视化:
import seaborn seaborn.distplot(train['charges'])
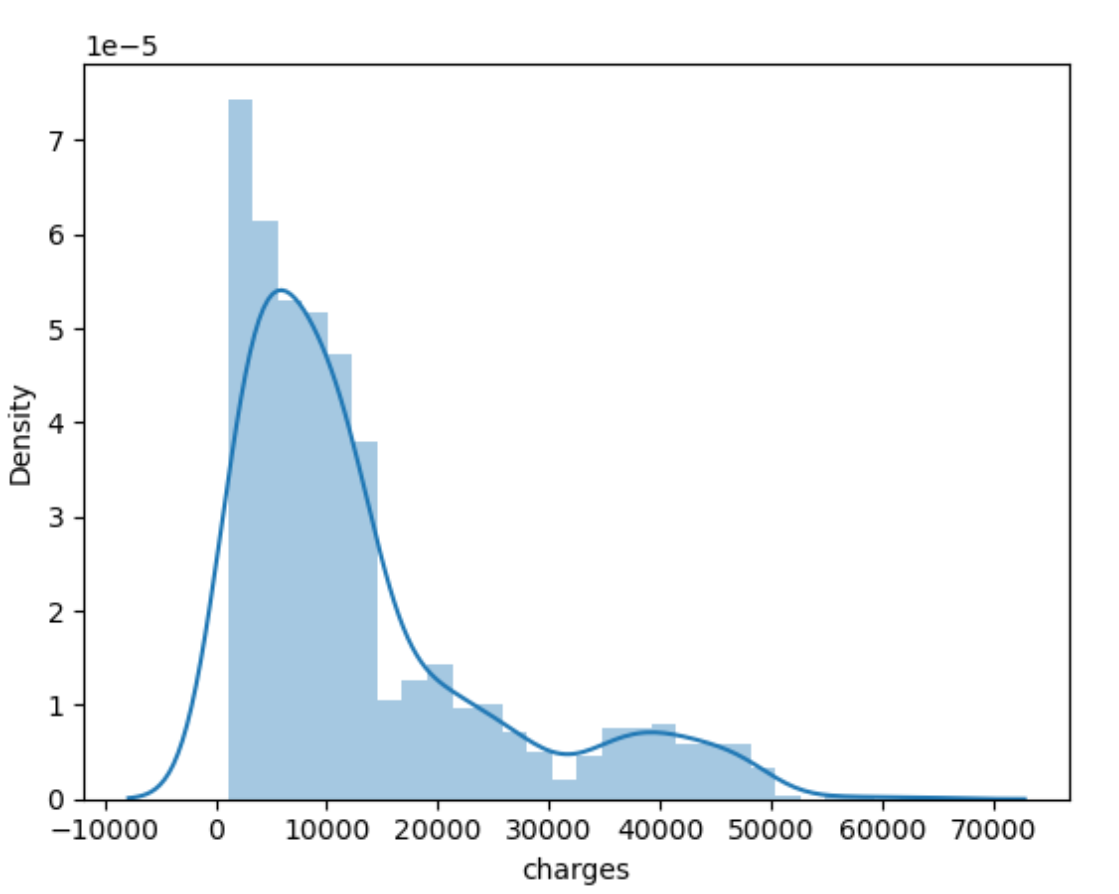
可以看出,charges近似符合对数正态分布,因此对charges取对数,再一次进行可视化charges的对数、age和bmi的可视化结果
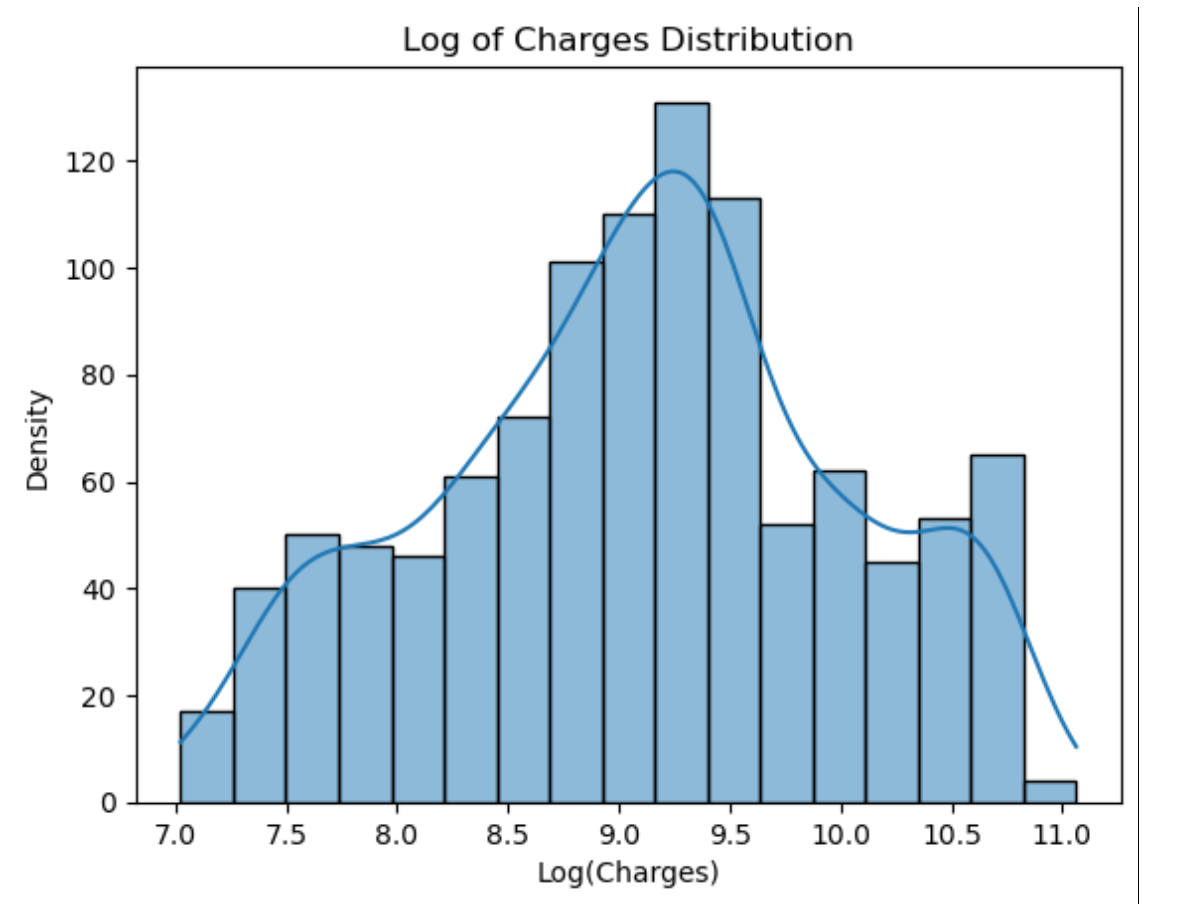
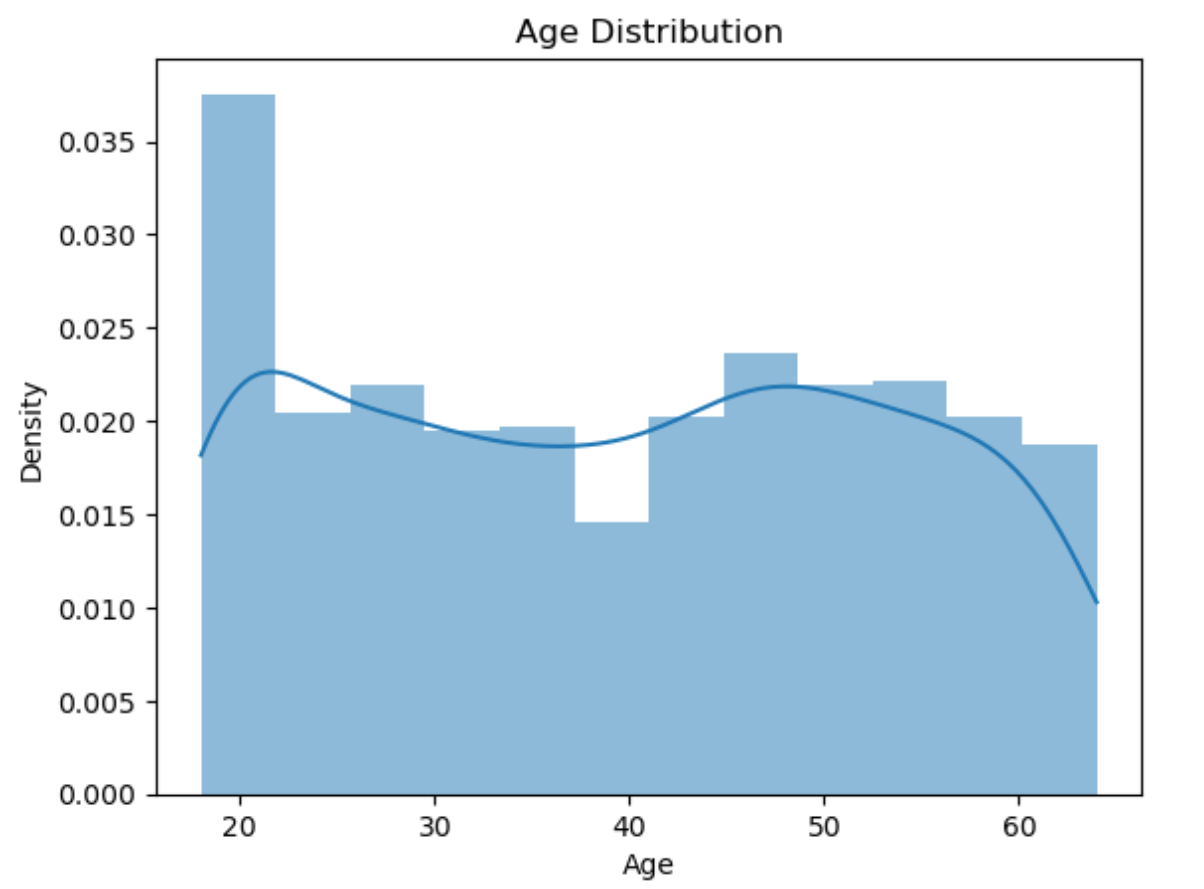
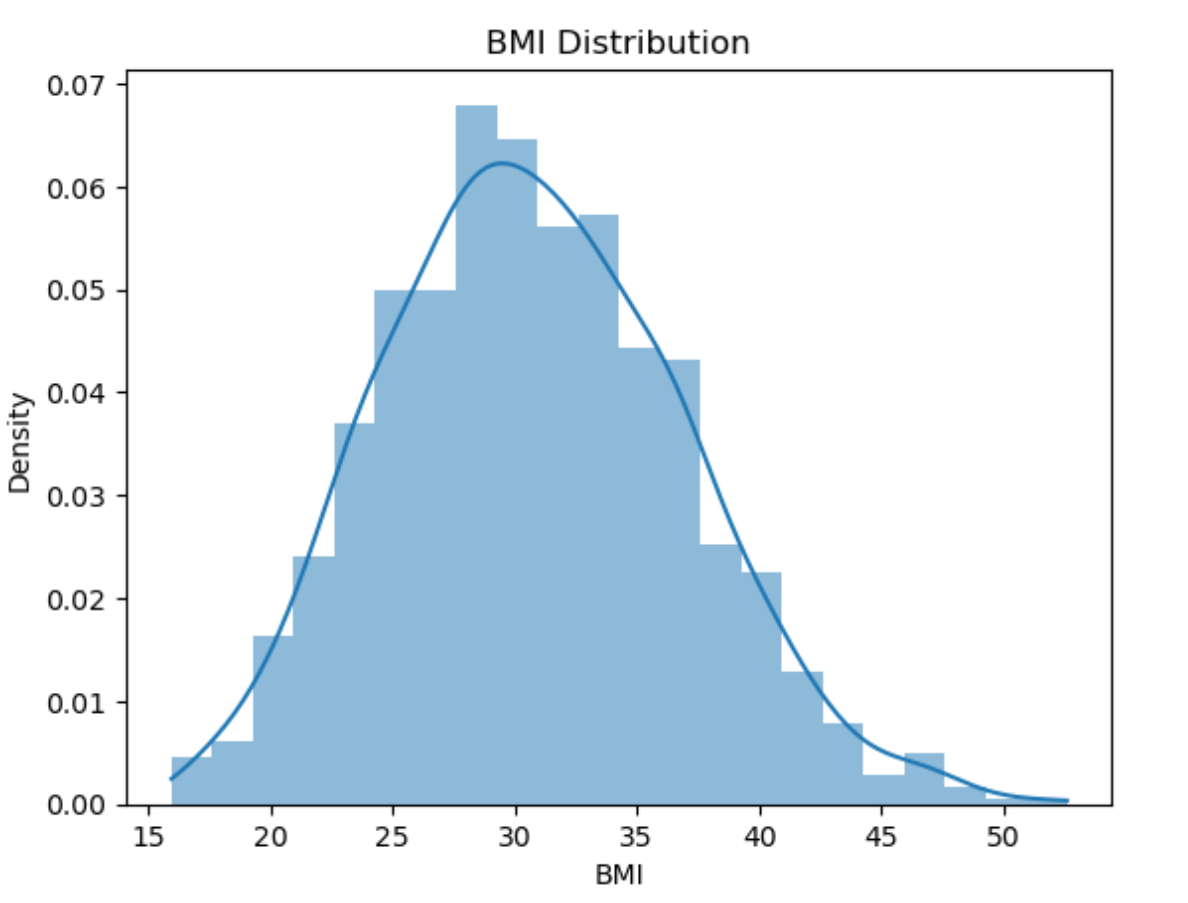
sns.pairplot(train[['log_charges', 'age', 'bmi']]) plt.show()
在这边我因为后文要进行线性关系分析,所以我想要是没有进行聚类,那么结果会是怎么样的。
在这边我运用了pairplot方法,他默认会为每一对变量生成散点图,即使这些变量之间可能没有明显的线性关系,生成了一个3阶图。
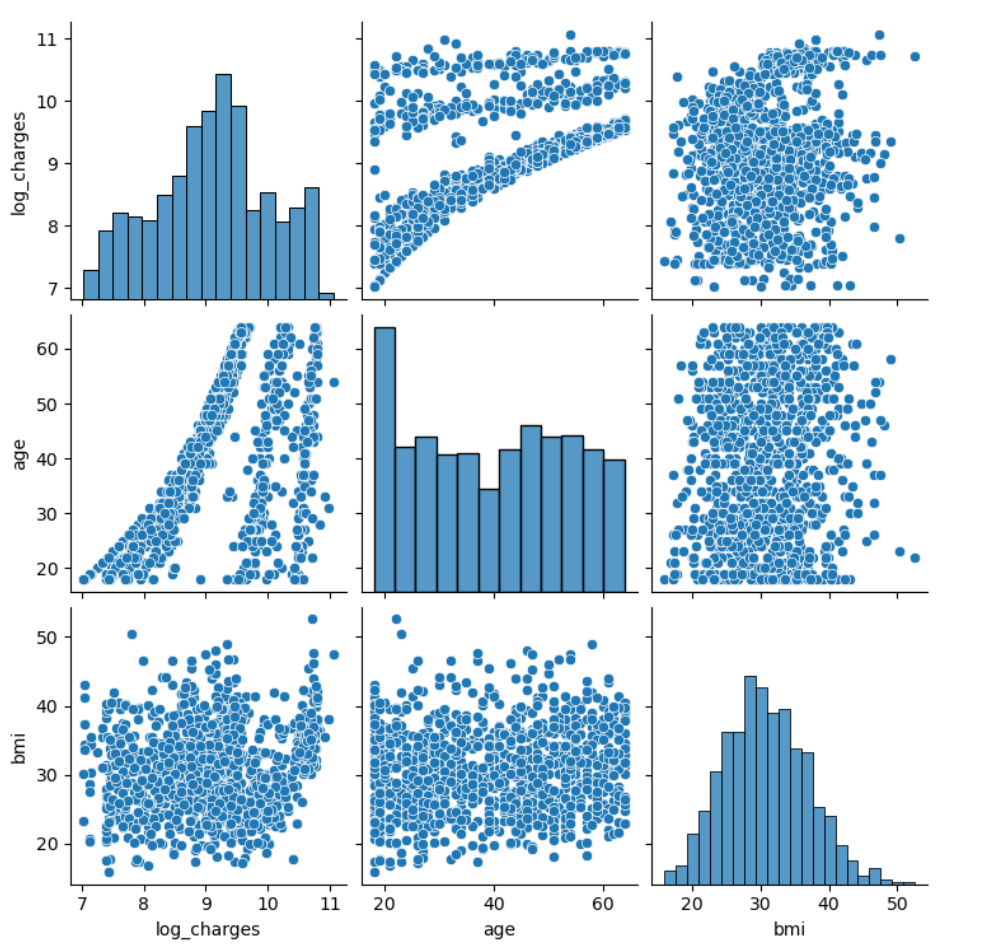
初步结果分析
其实所有聚类方法、线性回归模型,无非都是提高最后结果的精准度,但其实在聚类之前,我们已经可以看出来一点端倪,或者用结果分析更准确。
log_charges与age之间存在正相关关系,随着年龄的增加,log_charges也增加。- log_charges与bmi之间的关系不太明显,数据点分布较为分散,没有明显的相关性。
age与bmi之间也没有明显的相关性,数据点分布较为随机。
相互之间关系的差别,也直接提醒了我们:线性回归模型不能通过链接不同样本来建立,需要对每一个类样本自身进行线性建模,也就是说需要建立三个模型。
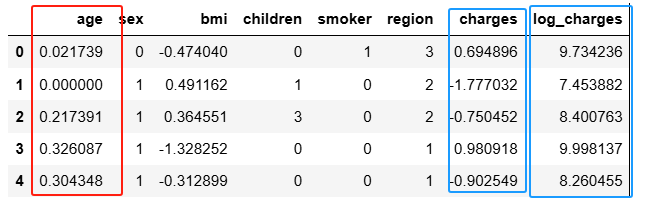
from sklearn.preprocessing import MinMaxScaler, StandardScaler min_max_scaler = MinMaxScaler() zscore_scaler = StandardScaler() train['charges'] = np.log(train['charges']) train[['age']] = min_max_scaler.fit_transform(train[['age']]) train[['bmi', 'charges']] = zscore_scaler.fit_transform(train[['bmi', 'charges']]) train.head(5)
Min-Max 归一化
使用最大最小值标准化将均匀分布的age映射到区间[0,1]
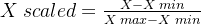
Z-score 标准化
log_chaeges和bmi服从正态分布,使用Z-score标准化方法映射取值
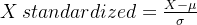
协方差矩阵和热力图
热力图有个有点,通过颜色很直接的反映多个变量之间相关性的强弱
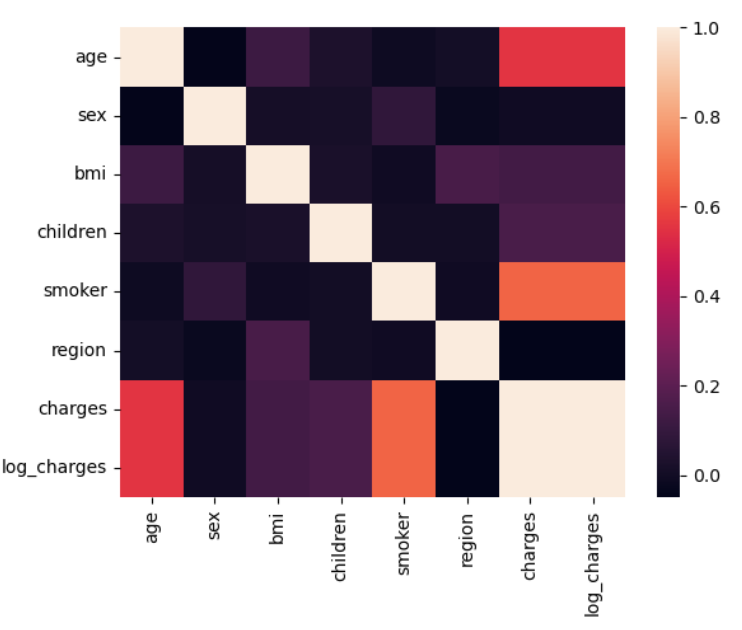
由图可以在我之前的散点图3阶图前面添加一点关系:smoker
DBSCAN聚类算法
针对于密度的聚类算法,通过指定一个虚径e和一个数量阈值M,构造一个圆,在半径范围内超过M数量的点集的点称为核心点;边界点是在半径内e内,但数量不超过M的点集的点;其余是噪点。
通过每个点的大量计算,这个对于人来说工作量太大,将所有核心点标记为同一类别,合成点集。
这边我做一个课外拓展:
大家有没有在概率论的课外学习中,或者竞赛中接触过一个很类似的分类方法,但不是用于聚类的(提示:也是用于求点的)
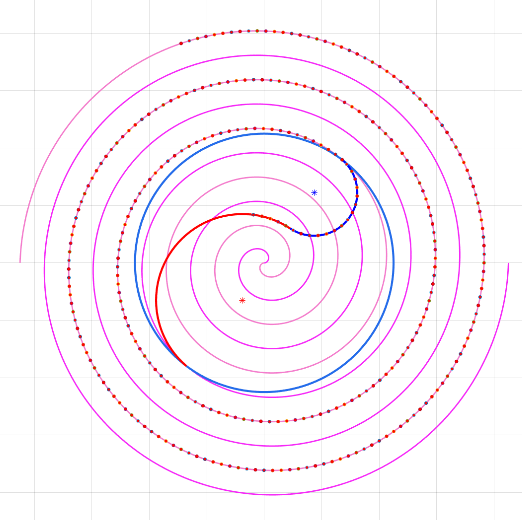
这边是2024年数学建模竞赛A题中的龙舟碰撞问题,这边除了利用四阶龙格库塔方法暴力迭代的方式,我当时想到了另外一种方法,利用蒙特卡洛方法随机生成点,给每个点赋以虚拟半径,随机给点,碰撞后就标红,最后,点最红的(也就是最密集的地方就是核心位置,类似于上述核心点)这样就可以利用其余的边界点和噪点规避碰撞。这俩个方法虽然解决的问题不一样,但是核心解决问题的方式一样,这么好的东西,我们不能仅仅学过就好了,应该内化于心,用于各个问题中实现他多方面的价值)
当然这里面的每一处都涉及数据分析,可视化,这方面也要紧紧掌握。
回归本实验:
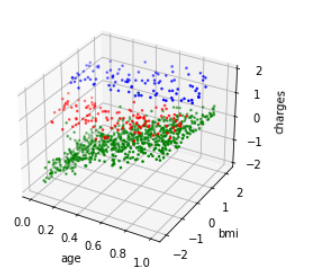
def graph3dc(train, x, y, z, type_name="type"): ax = plt.figure().add_subplot(111, projection = '3d') data = train[train[type_name] == 0] ax.scatter(data[x], data[y], data[z], s=10, c='r', marker='.') data = train[train[type_name] == 1] ax.scatter(data[x], data[y], data[z], s=10, c='g', marker='.') data = train[train[type_name] == 2] ax.scatter(data[x], data[y], data[z], s=10, c='b', marker='.') ax.set_xlabel(x) ax.set_ylabel(y) ax.set_zlabel(z) plt.show() graph3dc(train, 'age', 'bmi', 'charges')
样本分为3,再次分析age和charges关系
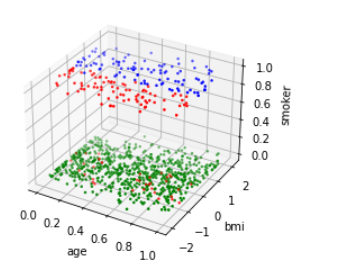
修改参数,观察age和smokers的聚类关系,从而再次验证age、smokers和charges的关系。
支持向量机分类算法
这边有需要提到上述的蒙特卡洛核心方法,因为他们取点分类的方法压根没有标准,所以仅仅适合得到标签,方便我们进行结果检验和方向选择,通过聚类方法我们知道了age、smokers和charges都有明显的关系,所以基于这个点,我们通过点集之间的相互的影响关系,设立最短距离标准,建立超平面,通过超平面对空间的点进行分类。
from sklearn.svm import SVC train_svm = train[train["type"] != -1] svm = SVC(kernel='linear') svm.fit(train_svm[["age", "bmi", "smoker"]], train_svm["type"]) train["type_predict"] = svm.predict(train[["age", "bmi", "smoker"]]) (train[train["type"] == train["type_predict"]]).shape[0] / train.shape[0]
利用非噪声点对支持向量机进行训练,将DBSCAN聚类的结果作为验证集来对比支持向量机,最后得出的结果约为83%。
线性回归
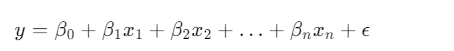
这是线性回归的标准方程
from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error train["age2"] = train["age"] ** 2 models = {} for t in train["type"].unique(): if t == -1: continue train_re = train[train["type"] == t] models[t] = LinearRegression() models[t].fit(train_re[["age", "age2", "bmi"]], train_re["charges"]) train["charges_predict"] = 0 for t in train["type_predict"].unique(): train.loc[train["type_predict"] == t, "charges_predict"] = \ models[t].predict(train.loc[train["type_predict"] == t, ["age", "age2", "bmi"]]) mean_squared_error(train["charges"], train["charges_predict"])
其实误差的含义很明显,真实值和预测值的对比,那么这边我们是如何确定预测值的
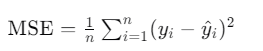
通过该公式,我们可以很明确的算出误差值。
这边我在数学理论检验中,发现一个问题,可能也会有人好奇,根据图像,大家很容易发现age和charges的关系并非简单的线性关系,看起来更像二次函数关系。
那么为什么可以利用线性回归呢?
这边涉及到一点线性代数的知识,也就是多项线性回归:他是线性回归的扩展,允许模型拟合数据中的非线性关系。
那么最后的一点疑惑我们也可以解决了。
结果预测
test = pd.read_csv("test.csv") submission = test.copy(deep=True)
test[['sex', 'smoker', 'region']] = \ encoder.transform(test[['sex', 'smoker', 'region']]) test[['age']] = min_max_scaler.transform(test[['age']]) test[['bmi', 'charges']] = zscore_scaler.transform(test[['bmi', 'charges']]) test["type"] = svm.predict(test[["age", "bmi", "smoker"]])
test["age2"] = test["age"] ** 2
for t in test["type"].unique():
test.loc[test["type"] == t, "charges"] = \models[t].predict(test.loc[test["type"] == t,
["age", "age2", "bmi"]])
test[["bmi", "charges"]] = zscore_scaler.inverse_transform(test[["bmi", "charges"]])
submission["charges"] = np.exp(test["charges"]) submission.to_csv('submission.csv', index=False)
补充:
在预测模型中,确定哪些变量对预测结果影响最大通常需要通过特征重要性分析来完成。特征重要性分析可以帮助我们理解模型预测中各个特征的贡献度。不同的模型和方法可能会提供不同的特征重要性指标。以下是一些常用的方法和模型来评估特征的重要性:
1)支持向量机(SVM):在SVM中,可以使用系数的绝对值或者核方法中支持向量的权重来评估特征的重要性。
2)线性模型(如线性回归、逻辑回归):在线性模型中,特征的重要性可以通过系数的大小来评估。系数的绝对值越大,特征对模型预测的影响越大。
3)决策树和随机森林:在决策树中,可以通过查看每个特征在树中作为分裂节点的次数来评估特征的重要性。随机森林模型会为每个特征提供一个重要性评分,这个评分是基于每个特征在构建多个决策树时降低不纯度的能力计算得出的。
4)梯度提升树(如XGBoost、LightGBM):这些模型提供了特征重要性指标,可以显示每个特征在模型中的贡献度。
5)基于模型的特征选择方法:可以使用递归特征消除(RFE)等方法来识别最重要的特征。
6)基于统计的特征选择方法:可以使用卡方检验、互信息、ANOVA等统计方法来评估特征与目标变量之间的关系强度。
结果分析
test = pd.read_csv("test.csv") seaborn.lineplot(data={'test': test["charges"], 'submission': submission["charges"]})
#使用seaborn的lineplot函数绘制test中的charges和submission中的charges的折线图,比较原始数据和预测结果

我们发现模型的预测值和真实值在一些峰值有差别,大致的曲线相同
这个差别,我们需要重回age2这个点、归一化和线性回归模型建立这几个方面。
标准差、方差、最小最大化、type、平均值、标准差、age2非线性化。
补充:
数据可视化是数据分析中非常重要的一部分,它可以帮助我们更直观地理解数据和结果。除了seaborn库中的lineplot函数外,Python中还有许多其他的库和方法可以用于数据可视化。以下是一些常用的库和它们提供的一些可视化方法:
1)Seaborn:
基于Matplotlib,提供了更高级的接口,用于绘制更复杂的统计图形。
常用方法:boxplot, violinplot, heatmap, pairplot, jointplot等。
2)Matplotlib:
这是Python中最基础的绘图库,提供了丰富的绘图功能。
常用方法:plot, scatter, bar, hist, boxplot, heatmap等。
3)Pandas:
Pandas内置了一些基于Matplotlib的绘图功能,可以直接在DataFrame上调用。
常用方法:plot, hist, boxplot, scatter等。
4)WordCloud:
用于生成词云的库,可以直观地展示文本数据中词汇的频率。
5)ggplot:
一个模仿R语言中ggplot2的Python库,提供类似的语法和功能。



