第一节 线性代数与方程的关系（笔记）

本笔记在Gilbert Strang教授教学基础上，增加了我自己的理解，如有不妥之处，还请大家批评指正。教授的学习视频如下：
方程组的几何解释

1、线性代数的基本问题

求解线性方程组是线性代数的基本问题。下面我们围绕一个二元一次方程组讨论相关内容。

\[\left\{\begin{matrix}2x-y=0 & \\ -x+2y=3 \end{matrix}\right. \]

2、从行图像理解方程组

从几何意义角度出发，方程组中每一个等式代表一个直线。
用python画出两个方程的图像：

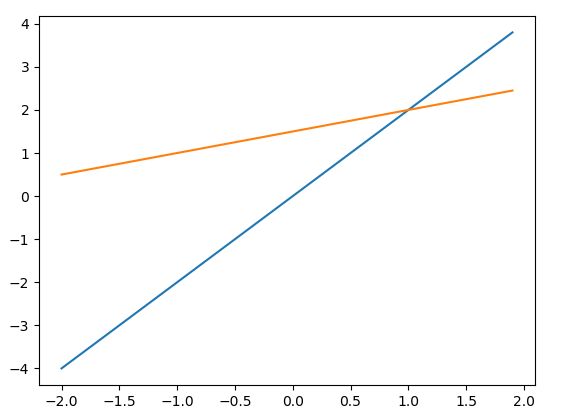
两条直线相交于(1,2)。

3、从列图像理解方程组

从系数角度来考虑问题，将变量和系数分开组成新的形式。

\[x\begin{bmatrix}2\\ -1\end{bmatrix}+y\begin{bmatrix}-1 \\ 2\end{bmatrix}=\begin{bmatrix}0 \\ 3\end{bmatrix} \]

变量x、y的系数都是以向量的形式表示。这两个向量经过x和y放大组合后变成向量

\[\begin{bmatrix}0 \\ 3\end{bmatrix} \]

(1,2)是方程组的解，此时的线性组合的图像如下：

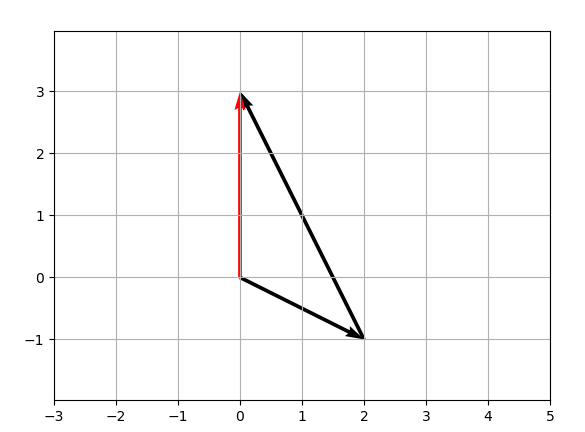
4、方程组的矩阵形式

我们再把列图像的代数形式进一步深化，也就是已知的方程组系数放一起，变量放一起，于是形成了系数矩阵和变量向量相乘的形式。

\[\begin{bmatrix}2& -1\\ -1& 2\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}0\\ 3\end{bmatrix} \]

令：

\[A=\begin{bmatrix}2& -1\\ -1& 2\end{bmatrix} \]

\[X=\begin{bmatrix}x\\ y\end{bmatrix} \]

\[b=\begin{bmatrix}0\\ 3\end{bmatrix} \]

方程组就简化成了：

\[AX=b \]

与此同时，我们发现了两种计算b的方式：

为什么X是列向量的形式而不是行向量的形式?
我们将AX=b简化成行和列的数量：A:(2,2)、X:(2,1)、b:(2,1)。在这样的组合中，A是2行,X是两行，相乘后b是2行；A是2列，X是1列，最后相乘b变成1列，我们可以理解为A决定b的行数，X决定b的列数。如果我们把X:(1,2),也就是行向量的形式[x, y]，那么A是2行，X是1行，相乘b是2行；而A是2列，X是2列，最后b却是1列，这个规则没法解释。

（1） 行计算

行计算是根据方程组获得。
其中:

\[0 = 2x-y \\3 = -x+2y \]

我们推广到一般的形式

\[b_{11}=A_{11}X_{11}+A_{12}X_{21} \\b_{21}=A_{21}X_{11}+A_{22}X_{21} \]

进一步我们可以推广到三元一次方程...

（2） 列计算

列计算的方式是根据方程组的向量组合形式获得

\[\begin{bmatrix}0\\ 3\end{bmatrix} = x\begin{bmatrix}2\\ 1\end{bmatrix}+y\begin{bmatrix}-1\\ 2\end{bmatrix} \]

b就是A中列向量的线性组合。

5、小结##

线性代数是由求解线性方程组引出。有两种理解方程组的形式：第一种是我们一直都学习的一个方程一个图像的形式，方程组的解就是这些图形相交的部分；第二种是向量的形式，向量形式将方程组简化为向量方程式，其解就是线性组合的系数。再第二种的基础上，又延伸出方程组的矩阵形式，这种形式将方程组中已知的系数和未知的变量从形式上区分开来。同时有行图像和列图像，我们理解了矩阵形式的乘法含义。