hashmap的泊松分布，二项式分布？
什么是二项式分布？
二项式分布就是只有两种结果的概率事件 在执行n次之后 某种结果的分布情况，就是n次伯努利实验，比如抛了n次硬币，k次正面的概率。
概率 = （k->n） p^k (1-p)^（n-k）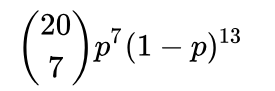
这种的抛20次 出现 7次正面的概率，p是每次抛出现正面的概率也就是0.5。
两个重点：
- 每次试验独立：第n次试验不受n-1次试验的影响，也不影响n+1次试验；
- 结果有且只有两个，并且互相对立：要么成功，要么失败，成功的概率+失败的概率=1；
这个就是二项式分布
什么是泊松分布？
是离散随机分布的一种，通常被使用在估算在 一段特定时间/空间内发生成功事件的数量的概率。泊松分布是二项分布p趋近于零、n趋近于无穷大的极限形式。
在某个时间/空间内出现的二项式分布。
就像这种，当n趋近于无线大的时候的概率。
二项式分布的期望是 E(x) = np = μ => p = μ/n 所以
=》
=》 
=》 
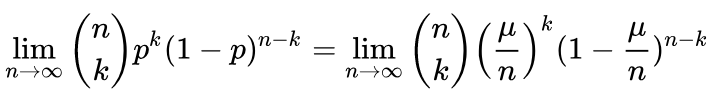
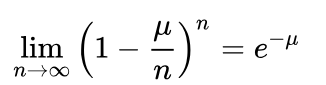
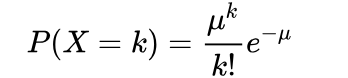μ=λ
说到这里其实要知道hashmap里面的阈值是 thershold = loadFactor*capacity 的；而默认的loadFactor是0.75，官网解释是说泊松分布算出来的，其实不然，这里泊松分布算出来的树出现的概率，当树化的阈值是8，加载系数是0.75的时候 出现树化的概率为 0 .00000006，jdk开发设计hashmap的时候，为了平衡树和链表的性能（树比链表遍历快，但是树的结点是链表结点大小的两倍，所以当树出现的概率比较小的时候的性价比就高了，所以取加载系数的时候平衡了下性能 取0.75）。平衡性能其实就是平衡时间与空间 个人认为。
- 原注释的内容和目的都是为了解释在java8 HashMap中引入Tree Bin（也就是放入数据的每个数组bin从链表node转换为red-black tree node）的原因
- 原注释：Because TreeNodes are about twice the size of regular nodes, we use them only when bins contain enough nodes to warrant use(see TREEIFY_THRESHOLD).
- TreeNode虽然改善了链表增删改查的性能，但是其节点大小是链表节点的两倍
- 虽然引入TreeNode但是不会轻易转变为TreeNode（如果存在大量转换那么资源代价比较大），根据泊松分布来看转变是小概率事件，性价比是值得的
- 泊松分布是二项分布的极限形式，两个重点：事件独立、有且只有两个相互对立的结果
- 泊松分布是指一段时间或空间中发生成功事件的数量的概率
- 对HashMap table[]中任意一个bin来说，存入一个数据，要么放入要么不放入，这个动作满足二项分布的两个重点概念
- 对于HashMap.table[].length的空间来说，放入0.75*length个数据，某一个bin中放入节点数量的概率情况如上图注释中给出的数据（表示数组某一个下标存放数据数量为0~8时的概率情况）
- 举个例子说明，HashMap默认的table[].length=16，在长度为16的HashMap中放入12（0.75*length）个数据，某一个bin中存放了8个节点的概率是0.00000006
- 扩容一次，16*2=32，在长度为32的HashMap中放入24个数据，某一个bin中存放了8个节点的概率是0.00000006
- 再扩容一次，32*2=64，在长度为64的HashMap中放入48个数据，某一个bin中存放了8个节点的概率是0.00000006
所以，当某一个bin的节点大于等于8个的时候，就可以从链表node转换为treenode，其性价比是值得的。
