最左匹配原则

写在前面：我在上大学的时候就听说过数据库的最左匹配原则，当时是通过各大博客论坛了解的，但是这些博客的局限性在于它们对最左匹配原则的描述就像一些数学定义一样，往往都是列出123点，满足这123点就能匹配上索引，否则就不能。但是我觉得编程不是死记硬背，这个所谓最左匹配原则肯定是有他背后的原理的。所以我尝试说明一下这个原理，这样以后用上优化索引的时候就不需要去记这些像数学定理一样的东西。了解原理比记住某些表面特点，我觉得是更聪明的方式。

1.简单说下什么是最左匹配原则
顾名思义：最左优先，以最左边的为起点任何连续的索引都能匹配上。同时遇到范围查询(>、<、between、like)就会停止匹配。
例如：b = 2 如果建立(a,b)顺序的索引，是匹配不到(a,b)索引的；但是如果查询条件是a = 1 and b = 2或者a=1(又或者是b = 2 and b = 1)就可以，因为优化器会自动调整a,b的顺序。再比如a = 1 and b = 2 and c > 3 and d = 4 如果建立(a,b,c,d)顺序的索引，d是用不到索引的，因为c字段是一个范围查询，它之后的字段会停止匹配。

2.最左匹配原则的原理
最左匹配原则都是针对联合索引来说的，所以我们有必要了解一下联合索引的原理。了解了联合索引，那么为什么会有最左匹配原则这种说法也就理解了。

我们都知道索引的底层是一颗B+树，那么联合索引当然还是一颗B+树，只不过联合索引的健值数量不是一个，而是多个。构建一颗B+树只能根据一个值来构建，因此数据库依据联合索引最左的字段来构建B+树。
例子：假如创建一个（a,b)的联合索引，那么它的索引树是这样的

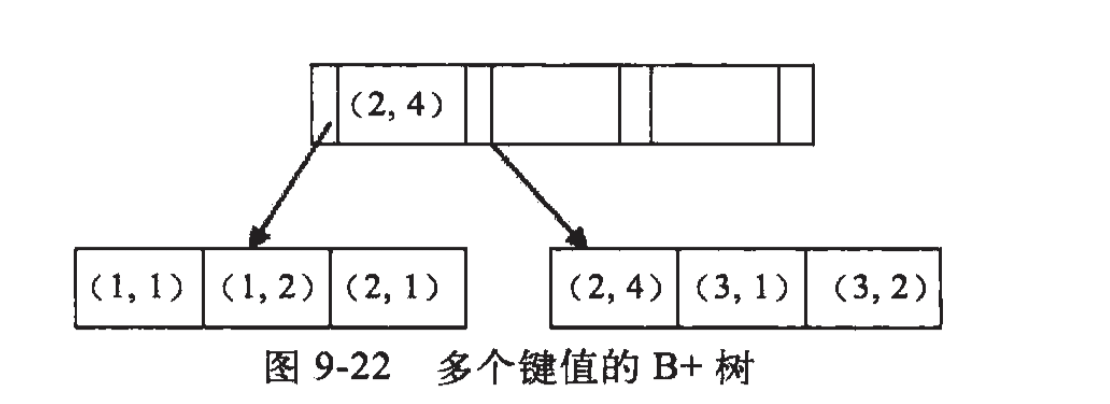
可以看到a的值是有顺序的，1，1，2，2，3，3，而b的值是没有顺序的1，2，1，4，1，2。所以b = 2这种查询条件没有办法利用索引，因为联合索引首先是按a排序的，b是无序的。

同时我们还可以发现在a值相等的情况下，b值又是按顺序排列的，但是这种顺序是相对的。所以最左匹配原则遇上范围查询就会停止，剩下的字段都无法使用索引。例如a = 1 and b = 2 a,b字段都可以使用索引，因为在a值确定的情况下b是相对有序的，而a>1and b=2，a字段可以匹配上索引，但b值不可以，因为a的值是一个范围，在这个范围中b是无序的。