64.最小路径和

2020-04-09

最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

题解:

思路1: 动态规划

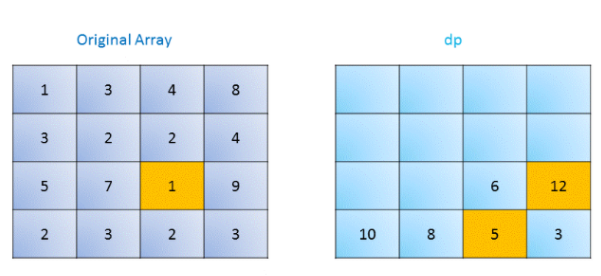
我们新建一个额外的 dpdp 数组，与原矩阵大小相同。在这个矩阵中，dp(i, j)dp(i,j) 表示从坐标 (i, j)(i,j)

到右下角的最小路径权值。我们初始化右下角的 dpdp 值为对应的原矩阵值，然后去填整个矩阵，对于每个元素考虑移动到右边或者下面，

因此获得最小路径和我们有如下递推公式：

dp(i,j)=grid(i,j)+min(dp(i+1,j),dp(i,j+1))

 

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function (grid) {
  let m = grid.length; // 行数
  let n = grid[0].length; // 列数
  let dp = Array(m).fill(0).map(x => Array(n).fill(0)); // 新建一个m行n列 全部为0 的空数组
  let r = 0; // grid[i][j]右边一个的值
  let b = 0; // grid[i][j]下面一个的值
  for (let i = m - 1; i >= 0; i--) {
    for (let j = n - 1; j >= 0; j--) {
      if (i === m - 1 && j === n - 1) {
        dp[i][j] = grid[i][j]; // 如果是最右下角的 那么直接赋值grid右下角的值
        continue;
      };
      
      b = i === m - 1 ? Number.MAX_SAFE_INTEGER : dp[i + 1][j]; // 如果是最后一行 最后一行没有下一行的元素所以是无限大
      r = j === n - 1 ? Number.MAX_SAFE_INTEGER : dp[i][j + 1]; // 如果是最后一列 最后一列没有右边的元素 所以是无限大
      dp[i][j] = grid[i][j] + Math.min(r, b); // dp[i][j]的值是他和右边和下面中较小的那个的和
    }
  }
  return dp[0][0];
};