加法器
加法器
1.1 半加器
半加器用于计算2个单比特二进制数a与b的和,输出结果sum(s)和进位carry(c)。在多比特数的计算中,进位c将作为下一相邻比特的加法运算中。单个半加器的计算结果是2c+s。其真值表、逻辑表达式、verilog描述和电路图分别如下所示。
逻辑表达式:
$$s=a'b |ab'$$
$$c=ab$$
module half_adder( input a, input b, output c, output s); assign c=a&b; assign s=a^b; endmodule//verlog描述
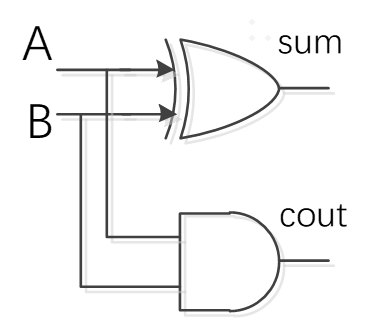
1.2 全加器
全加器不同于半加器的地方是:全加器带有进位输入cin。输入为a,b,cin, 输出为sum(s)和carry(cout),均是单比特信号。s为a,b,cin三个单比特数的和,cout为a,b,cin三个数超过2后的进位。真值表、逻辑表达式、verilog描述和电路图分别如下所示。
module full_adder( input A, input B, input CI, output CO, output S); assign CO= CI&(A^B)|A&B; assign S=A^B^CI; endmodule//verlog描述

$$CI(A^B)+AB=CI(AB+A'B)+AB=AB'CI+A'BCI+ABCI+AB=ACI+BCI+AB=CI(A+B)+AB$$
逻辑表达式:
$$s=a^\prime bcin^\prime+ab^\prime cin^\prime+a^\prime b^\prime cin+abcin$$
$$=cin^\prime(a^\prime b+ab^\prime)+cin(a^\prime b+ab^\prime)^\prime$$
$$=a⊕b⊕cin$$
$$cout=abcin^\prime +a^\prime bcin+ab^\prime cin+abcin=ab+acin+bcin$$
$$cout= ab+ (cin (a⊕b))$$

传统六门方案
1.3 行波进位加法器RCA
N-bit加法器可以根据1-bit全加器组合而成。每个全加器的输出进位cout作为下一个全加器的输入进位cin,这种加法器称为行波进位加法器(Ripple-carry adder,简称RCA).
module rca_add#(parameter DIN=4)( input [DIN-1:0] add_A, input [DIN-1:0]add_B, input CI, output [DIN-1:0] S, output COUT ); wire [DIN:0] C_temp; assign C_temp[0]=CI; assign COUT=C_temp[DIN]; generate genvar i;
for(i=0;i< DIN-1;i=i+1) begin full_adder u( .A(add_A[i]), .B(add_A[i]), .CI(C_temp[i]) .S(S[i]) .COUT(C_temp[i+1]) ); end endgenerate endmodule
如一个4比特加法器的结构如上图所示,其中A,B为4比特的加数,S为A+B的和,cout为该加法器的进位输出。
从输入a,b,cin到输出s和cout,有以下路径:
a->s:经过xor1,xor2两个门电路
b->s:经过xor1,xor2两个门电路
cin->s:经过xor2一个门电路
a->cout:经过xor1,and1,or1三个门电路
b->cout:经过xor1,and1,or1三个门电路
cin->cout:经过and2,or1两个门电路
由这些路径可知,从a,b,cin输入数据准备好,到所有的s和cout完成,a或b到cout共有三个门电路延迟,是全加器的最长路径,且s不参与下一级全加器运算,cout将作为下一个cin输入继续计算下一级的s和cout。
由上图可以看出得到进位cout的结果依赖于c3,c2,c1,c0,对于32-bit,64-bit,128-bit等加法器,进位链将显得更加长。所以,行波进位加法器设计简单,只需要级联全加器即可,但它的缺点在于超长的进位链,限制了加法器的性能。

每一个全加器计算的时候必须等待它的进位输入产生后才能计算,所以16个全加器并不是同时进行计算的,而是一个一个的串行计算。这样会造成较大的延迟。
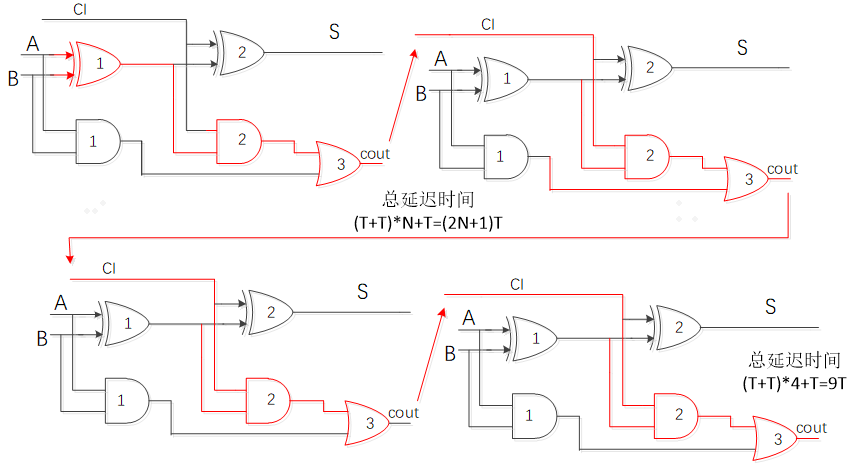
由N个全加器级联的行波进位加法器除了第一个进位c1有3个门延迟外,剩余N-1个全加器生成进位需要2个门电路延迟,所以N比特行波进位加法器最长路径共有“(3+(N-1)*2)=2N+1”个门电路延迟,如上图4比特行波进位加法器,红色描绘的路径即是最长路径,共有2*4+1=9个门电路延迟。每增加一位,增加一个与门和或门的延时,$t_{adder}=(N-1)*t_{carry}+t_{sum}$
进位旁路/跳跃加法器CSKA
进位旁路加法器(Carry Skip Adder,CSA,CSKA),也称Carry Bypass Adder。进位旁路加法器的思想在于加速进位链的传播,在某种情况下,到达第i位的进位无需等待第i-1位进位。在4比特RCA中,最长的进位链为c0->c1->c2->c3->c4,也就是说,每一位全加器都有进位,这条路径也是最长的关键路径。进位旁路加法器通过加入旁路逻辑来缩短这条最长路径,该旁路逻辑由2选1数据选择器,第x级进位和第y级进位和进位bypass信号组成。
由Mbit级联构成的Nbit进位旁路加法器的关键路径延迟为:
$$t_{add}=t_{setup}+M*t_{carry}+(N/M-1) t_{skip}+M*t_{carry}+t_{sum}$$
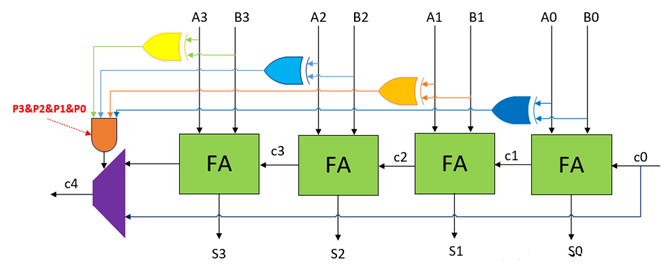
根据RCA: P3&P2&P1&P0=1时c4=c0;进位c0直接传播至c4,而不需再经过4级全加器的延迟,这就是进位旁路加法器的核心。下面分析P3&P2&P1&P0=1时,c0可以直接传播至c4的原因,先看c4的生成逻辑:
$$c_4=G_3+c_3 P_3=G_3+(G_2+G_1 P_2+G_0 P_1 P_2+c_0 P_0 P_1 P_2 ) P_3=G_3+G_2 P_3+G_1 P_2 P_3+G_0 P_1 P_2 P_3+c_0 P_0 P_1 P_2 P_3$$
当P3&P2&P1&P0=1时,则$P3=P2=P1=P0=1$,所以c4生成逻辑如下:
$$c_4=G_3+G_2+G_1+G_0+c_0$$
在介绍超前进位加法器中,我们定义了PG:
$$P_i=a_i⊕b_i, i=0,1,2,…,N-1$$
$$G_i=a_i b_i, i=0,1,2,…,N-1$$
P是a与b异或的结果,只有a=0,b=1或者a=1,b=0时,P才可能等于1,而G=ab,所以只要P=1,G则一定为0,所以G3=G2=G1=G0=0。最后结论与上述一致:当P3&P2&P1&P0=1时,c4的生成逻辑最终变成c4=c0。由Mbit级联构成的Nbit进位旁路加法器的关键路径延迟为:
$$t_{add}=t_{setup}+M*t_{carry}+(N/M-1) t_{skip}+M*t_{carry}+t_{sum}$$
以上关键路径发生在:c0走第一级Block,经过4级全加器,进位从bit0到bit3生成c4,中间进位经过bypass逻辑。最后一级走Block逻辑,经过4级全加器,进位从bit12到bit15生成c16.其中:
Tsetup:A,B低位到第一级block的时间
tcarry:每个进位传播Block中全加器产生进位的时间
Tskip:进位通过skip逻辑的时间
Tsum:从最后个进位到S输出的时间

16比特CSKA结构
可能在此处读者会有一个疑问,为什么最长的delay会是中间两级路径,如果加法器进位全部走Block逻辑,应该具有更长的延迟啊?其实走最长的路径,中间路径会被旁路,也就是执行0111_1111_1111_1111 + 0000_0000_0000_0001的情况,此时中间两级的P都为1,所以中间两级进位被旁路。第一级进位产生后,中间两级被旁路,最后一级经过RCA进位链,也就是下图中红色描绘出的路径图。

16比特CSKA关键路径图
1.3.1 进位旁路加法器关键路径与优化
将N比特加法器,以m比特为一组,分成N/m组,如下式16比特进位旁路加法器,N=16,m=4,共有4组,该16比特CSKA由4比特CSKA级联而成,其中4比特CSKA由4个全加器组成的Block,进位逻辑Skip logic和2选1数据选择器三部分组成。
module cska_add #(width=16) ( input [width-1:0] add_A, input [width-1:0] add_B, input CI, output [width-1:0] SUM, output CO ); wire [width>>2:0] C; assign C[0] = CI; assign CO = C[width>>2]; genvar i; generate for( i=0; i<width>>2; i=i+1) begin cska_4bit u_cska_4bit ( .add_A(add_A[i*4+3:i*4] ), .add_B(add_B[i*4+3:i*4] ), .CI(C[i] ), .SUM(SUM[i*4+3:i*4] ), .CO(C[i+1])); end endgenerate endmodule module cska_4bit#(parameter width=4)( input [width-1:0] add_A, input [width-1:0] add_B, input CI, output [width-1:0] SUM, output CO ); wire[width:0]C; wire[width-1:0]P; assign C[0]=CI; genvar i; generate for( i=0; i<width; i=i+1) begin full_adder_cska u_full_adder_cska( .A ( add_A[i] ), .B ( add_B[i] ), .CI ( C[i] ), .CO ( C[i+1] ), .S ( SUM[i] ), .P ( P[i] ) ); end //carry bypass assign sel = P[0] & P[1] & P[2] & P[3]; assign CO = sel ? CI : C[width]; endgenerate endmodule module full_adder_cska( input A, input B, input CI, output CO, output S, output P ); assign CO= CI&(A^B)|A&B; assign S=A^B^CI; assign P=A^B; endmodule
1.4 超前进位加法器LCA
对于更宽的加法器N,行波进位加法器关键路径越长,限制了加法器的性能,对于高速处理器等将是个极大的瓶颈。所以,超前进位加法器(Lookahead Carry Adder,简称LCA)可以优化改进行波进位器的关键路径。RCA的缺点在于第k位的进位Ck必须依赖于前一级的Ck-1,所以最高位的进位将必须等待之前所有级进位计算完毕后才能计算出结果。所以,超前进位加法器的思想是并行计算进位Ck。
s=a^b^cin
cout= a&b|(cin &(a^b))
观察上式s和cout,将共有部分分别定义:P= a^b ; G=a&b
对于N比特LCA加法器,进位与和公式将重新书写如下:
假设输入a[N-1:0],b[N-1:0], c0=cin;
$$s_i=P_i⊕c_i$$
$$c_{i+1}=G_i+c_i P_i$$
$$c_0=c_{in}$$
$$c_{out}=c_N $$
$$其中P_i=a_i⊕b_i i=0,1,2,…,N-1$$
$$G_i=a_i b_i i=0,1,2,…,N-1$$
其中进位传播项$P_i$由一个与第i位输入相关异或门实现, 进位生成项$G_i$由一个与第i位输入相关的与门实现。以4比特LCA加法器为例,其进位链与和公式分别计算如下:
输入进位为 ,a[N-1:0],b[N-1:0]:
$$c_1=G_0+c_0P_0$$
$$c_2=G_1+c_1P_1=G_1+(G_0+c_0 P_0)P_1=G_1+G_0 P_1+c_0 P_0 P_1$$
$$c_3=G_2+c_2 P_2=G_2+(G_1+G_0 P_1+c_0 P_0 P_1)P_2=G_2+G_1 P_2+G_0 P_1 P_2+c_0 P_0 P_1P_2$$
$$c_4=G_3+c_3 P_3=G_3+(G_2+G_1P_2+G_0 P_1 P_2+c_0 P_0 P_1 P_2 )P_3$$
$$=G_3+G_2 P_3+G_1 P_2 P_3+G_0P_1P_2P_3+c_0 P_0 P_1 P_2 P_3 )$$
$$s_0=P_0⊕c_0$$
$$s_1=P_1⊕c_1$$
$$s_2=P_2⊕c_2$$
$$s_3=P_3⊕c_3$$
根据上述式子,可以计算出从输入所有的a,b和c0,LCA的输出进位c4只需要3级门电路延迟,c0,c1,c2,c3同时生成,同时由于S3=P3^c3,所以4比特LCA关键路径为4级门延迟。Ci和Si,其结构图为:
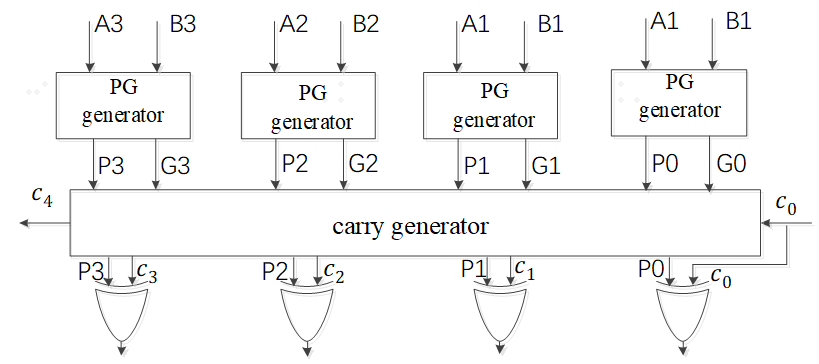

从输入所有的a,b和c0,LCA的输出进位c4只需要3级门电路延迟,c0,c1,c2,c3同时生成,同时由于S3=P3 xor c3,所以4比特LCA关键路径为4级门延迟。虽然经过了很多门电路,但他们的计算是同时的,而4比特RCA计算出c4需要9个门电路延迟。同样是32比特加法器,理想的LCA(全部展开所有的进位逻辑)关键路径延迟理论上只需要4个门电路,而RCA的关键路径延迟为65个门电路。如果采用4比特级联LCA,形成32比特LCA,则需要(3+7*2+1)=18级门电路延迟,相比RCA,缩短了关键路径的长度。
以上比较忽略多输入门延迟,真正的门电路延迟计算需根据不同的门电路库文件,且对AND/OR/NAND等门电路输入数目有限制,如通常的4输入。此处只可意会。
总而言之,RCA的缺点在于关键路径长,限制了速度,性能不高;LCA关键路径短,速度快,进位链计算依赖少,但对于位宽较大的加法器,PG和进位生成逻辑大,存在较大扇入扇出,变化信号多,会有较多的glitch,且面积与复杂度比同等的RCA大。
RCA的缺点在于关键路径长,限制了速度,性能不高;RCA的缺点在于关键路径长,限制了速度,性能不高;LCA关键路径短,速度快,进位链计算依赖少,但对于位宽较大的加法器,PG和进位生成逻辑大,存在较大扇入扇出,变化信号多,会有较多的glitch,且面积与复杂度比同等的RCA大。
$C[0]=CI$
$C[1]=G[0]+C[0]P[0]$
$C[2]=G[1]+G[0]P[1]+C[0]P[0]P[1]$
$C[3]=G[2]+G[1]P[2]+G[0]P[1]P[2]+C[0]P[0]P[1]P[2]$
$C[4]=G[3]+G[2]P[3]+G[1]P[2]P[3]+G[0]P[1]P[2]P[3]+C[0]P[0]P[1]P[2]P[3]$
/* assign SUM[0]=P[0]^C[0]; assign SUM[1]=P[1]^C[1]; assign SUM[2]=P[2]^C[2]
assign SUM[3]=P[3]^C[3]*/
module lca_add( input[3:0] add_A, input[3:0] add_B, input CI, output[3:0]SUM, output CO ); wire [4:0]C; wire [3:0]G; wire [3:0]P; assign P=add_A^add_B; assign G=add_A&add_B; assign C[0]=CI; assign C[1]=G[0]|C[0]&P[0]; assign C[2]=G[1]|C[1]&P[1]; assign C[3]=G[2]|C[2]&P[2]; assign C[4]=G[3]|C[3]&P[3]; assign SUM=P^C[3:0]; assign CO=C[4]; endmodule
1.5 混合型超前进位加法器
对于位宽更大的LCA如16,32,64比特LCA等可以并行生成所有的PG和进位C,但这会造成电路极大的扇入和扇出;另外可以根据4比特LCA级联而成,如16比特LCA可由如下图级联而成(属RLCA):

1.6 进位选择加法器CSA
进位选择加法器(Carry Select Adder)由2个行波进位加法器和选择器构成,其中一个RCA加法器假定进位为0,另外一个RCA加法器假定进位为1,其结构如下
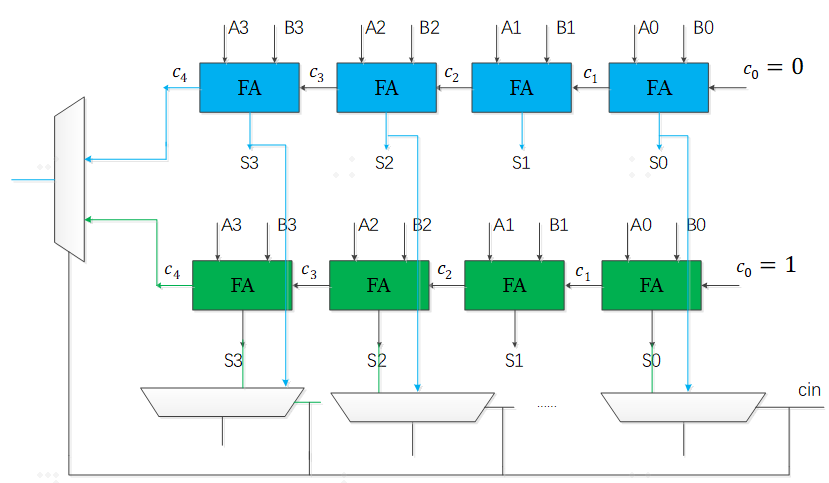
上面一排蓝色4个全加器组成的RCA,假定进位输入c0=0;下面一排青色4个全加器组成的RCA假定进位输入c0=1。如果来自低级的进位cin为0,则选择上面蓝色的进位c4作为该加法器的进位输出;如果来自低级的进位Cin为1,则选择青色RCA的进位c4作为该加法器的进位输出。同时Cin作为选择器选择信号,控制S3~S0的输出来自于蓝色RCA还是绿色RCA。
如下图16比特进位选择加法器,以4比特进位选择加法器为结构级联,每一级的进位可以同时经过4个全加器延迟同时生成,而选择信号在经过最低位的4比特RCA后生效,经过三个数据选择器的延迟,c16就会生成。所以,相比于同等16比特的行波进位加法器,进位选择加法器极大地提高了速度,是面积换取速度设计的典型代表。
由Mbit级联构成的Nbit进位选择加法器的关键路径延迟为:
$$t_{add}=t_{setup}+Mt_{carry}+N/M t_{mux}+t_{sum}$$
Tsetup:A,B低位到第一级block的时间
tcarry:每个RCA Block中全加器产生进位的时间
T :进位通过mux逻辑的时间
Tsum:从最后一个进位到S输出的时间
//two RCAS and Carry and Sum Select module csea_add #(width=16)( input [width-1:0] add_A, input [width-1:0] add_B, input CI, output [width-1:0] SUM, output CO ); wire [width-1:0]sum_sel0; wire [width-1:0]sum_sel1; wire [4:0]select; wire [4:0]c_sel0; wire [4:0]c_sel1; assign c_sel0[0]=0; assign c_sel1[0]=0; assign select[0]=CI; assign sum_sel1[3:0]=sum_sel0[3:0]; assign CO= select[4]; genvar i; generate for (i=0;i<width>>2;i=i+1) begin if (i==0)begin ripple_add u_csea_4bit_c0( .add_A(add_A[3:0]), .add_B(add_B[3:0]), .CI(select[0]), .SUM(sum_sel0[3:0]), .CO(select[1]) ); assign SUM[3:0]=sum_sel0[3:0]; end else begin ripple_add u_csea_4bit_sel0( .add_A(add_A[i*4+3:i*4]), .add_B(add_B[i*4+3:i*4]), .CI(1'b0), .SUM(sum_sel0[i*4+3:i*4]), .CO(c_sel0[i+1]) ); ripple_add u_csea_4bit_sel1( .add_A(add_A[i*4+3:i*4]), .add_B(add_B[i*4+3:i*4]), .CI(1'b1), .SUM(sum_sel1[i*4+3:i*4]), .CO(c_sel1[i+1]) ); assign select[i+1]=select[i] ? c_sel1[i+1] : c_sel0[i+1]; assign SUM[i*4+3:i*4]= select[i]? sum_sel1[i*4+3:i*4] : sum_sel0[i*4+3:i*4]; end end endgenerate endmodule
进位选择加法器总结:
优势:对于更大位宽加法器高位进位不取决于进位传播,速度更快。但正确的输出必须等待正确的进位选择信号输出。
缺点:电路面积花费巨大,对于N比特加法器,需要几乎比RCA翻倍的全加器个数和许多多余的数据选择器。
另外对于N比特进位选择加法器构成的基础块,其大小可以相同,也可以不同,即其中的RCA全加器个数可以不同。
由进位选择加法器组成的加法器器又称为Conditional Sum Adder。
进位保存加法器
进位保存加法器(Carry Save Adder,CSA),使用进位保存加法器在执行多个数加法时具有极小的进位传播延迟,它的基本思想即将3个加数的和减少为2个加数的和,将进位c和和s分别计算保存,并且每比特可以独立计算c和s,所以速度极快。
在许多加法计算中,一般有2个以上,或者更多的加数。
如: Sum = A + B + C + D + E + …
最直接的办法是:先将A+B结果计算出来,再与C计算,依次进行,而进位保存加法器将进位Carry与和Sum分开计算,计算步骤如下:
(1)计算和Sum:每一列数相加,对进制数取模(取余数),此处为二进制,如(0+1+0)=1,(0+1+1)=0,(1+1+1)=1。
(2)计算进位Carry:从竖式低位开始计算,低位向高位进位,每一列的数相加对进制数取商。如下式中,(0+1+0)/2 = 0 … 1,(1+1+0)/ 2 = 1 … 0,忽略余数。低位向高位传递进位。
(3)如下式子中,3个数的和变成了2个数的和,Carry和Sum,分别是11100和00001,注意,此处Carry是11100不是1110,因为是低位往高位进位,最低位进位为0,从竖式也可以看出,对Carry和Sum相加,结果仍然是11101,即29。

对于m个数相加,每个数n比特宽,总共需要m-1次加法。假如使用超前进位加法器LCA的话,直接相加法总共需要的门延迟为O(lgn);如果使用CSA树形加法器,门延迟将变为O(lg m * lg n)。
使用进位保存加法器CSA结构则可以将门延迟降到更低,其结构如上图(2)所示,它将3个数相加转换为2个数相加,在树的根部,加数宽度变为O(n+log m),因此如果最后一个加法器用LCA的话,则门延迟为O(lg(n+lg m))。
如果最低位相加并对2取商后为1,则该C[i]应该是C[1],C[0]总是为0,当前级的进位结果计算完之后应该写到前一级,
module csa_add #(width=4) (
input [width-1:0] add_A,
input [width-1:0] add_B,
input [width-1:0] add_C,
input CI,
output [width:0] c;
output [width:0] s;
output [width:0] SUM,
output CO
);
assign c[0]=0;
assign s[width]=0;
genvar i;
generate
for(i=0; i<width; i=i+1) begin
full_adder u_full_adder(
.A ( add_A[i] ),
.B ( add_B[i] ),
.CI ( add_C[i] ),
.CO ( c[i+1] ),
.S ( s[i] )
);
end
endgenerate
wire [width+1:0] cout_temp; wire [width:0] SUM;
assign cout_temp[0]=CI;
assign CO=cout_temp[width+1];
genvar k;
generate
for(k=0; k<width+1; k=k+1) begin
full_adder u_full_adder(
.A ( c[k] ),
.B ( s[k] ),
.CI (cout_temp[k] ),
.CO (cout_temp[k+1] ),
.S ( SUM[k] )
);
end
endgenerate
endmodule//verlog描述
module full_adder(
input A,
input B,
input CI,
output CO,
output S
);
assign CO= CI&(A^B)|A&B;
assign S=A^B^CI;
endmodule//verlog描述
1.7 3:2 Compressor
3:2 Compressor是进位保存加法器的一种,它将三个数的和转换为2个数的和,根据算式的行为,列出其真值表如下:
|
输入 |
输出 |
|||
|
a |
b |
cin |
s |
cout |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
3:2 Compressor其实就是一个全加器,所以只要将全加器的进位作为一个其中一个加数输入,经过如下的变换,就可以将全加器FA生成进位保存加法器CSA。
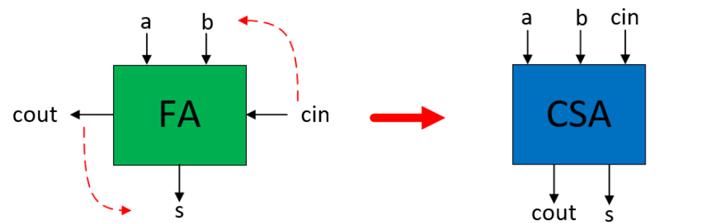
三个32比特的数x,y,z相加,其CSA结构如下:
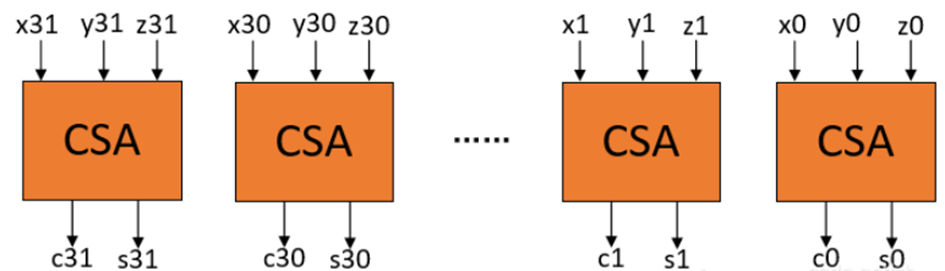
在使用verilog设计一个算式如Sum = A + B + C + D;则可以设计一个全加器,由全加器组成N比特的CSA结构,将多个数合并,经过两级CSA,最后将进位C[N-1:0]与和Sum[N-1:0]通过一个加法器相加,注意进位传入到任何模块中时,需要将C[N-1:0]乘以2,因为这是它合并后真正的数。


