第04次作业-树

1.学习总结

1.1树结构思维导图

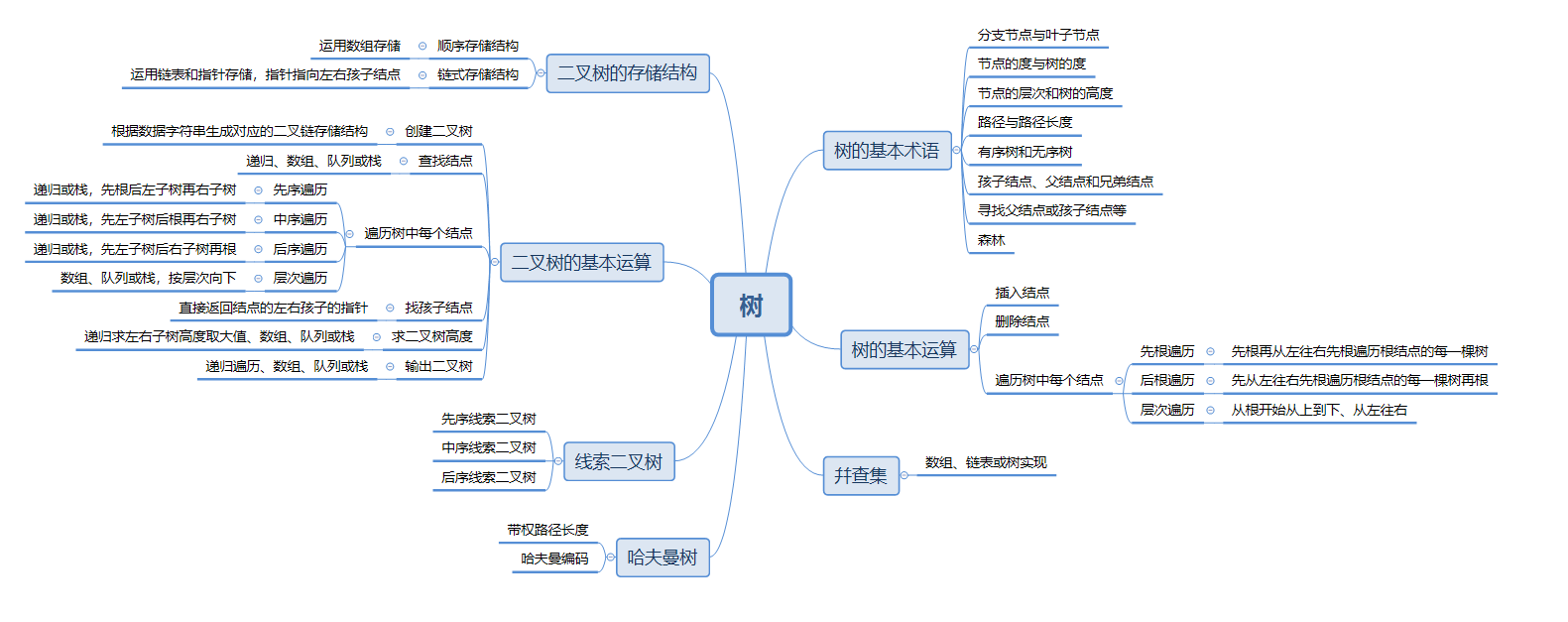
1.2 树结构学习体会

对树结构的认识：树的结构是一种非线性结构，数据元素之间是一对多的关系，解决关于树的问题时可以用递归、栈、数组、队列。
遇到的困难：树的操作不熟练，解决树的问题可以运用递归、栈、数组、队列，解题方式多样，难以运用自如。
树结构可以解决的问题：哈夫曼编码、家谱处理、表达式处理

2.PTA实验作业

题目1：7-8 jmu-ds-二叉树叶子结点带权路径长度和

1. 设计思路

构造树
先序遍历二叉树，若树不为空找到叶子结点(左右子树均为空的结点)
带权路径长度和=每个叶子（(结点深度-1)*权重)之和

2.代码截图

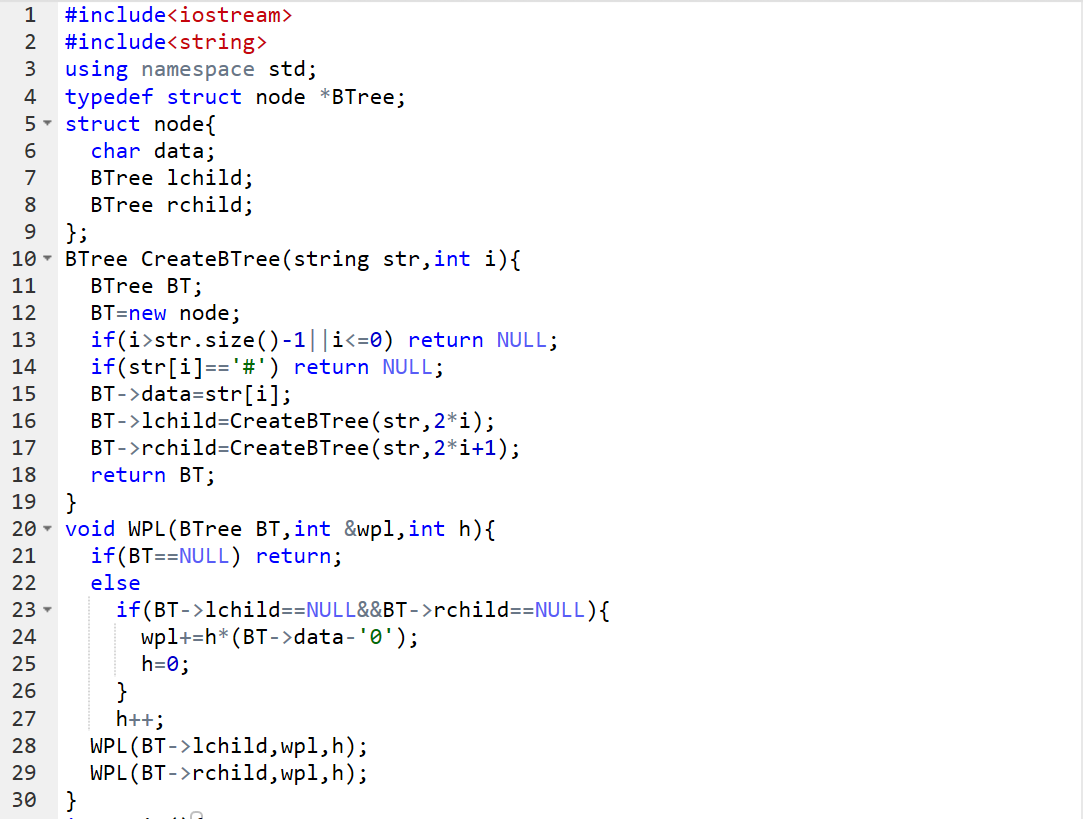
3. PTA提交列表说明。

题目2：6-4 jmu-ds-表达式树

1. 设计思路

建立表达式二叉树：
依次判断读入字符串的字符
若字符为操作数，创建结点并入操作数栈
若字符为运算符，判断运算符栈栈顶运算符与该运算符优先级
若该运算符优先级高，该运算符入运算符栈
若该运算符优先级低，运算符栈顶两个符号出栈并创建结点入栈
运算符栈栈顶运算符与该运算符优先级相同，栈顶运算符出栈
取出两个操作数和一个运算符出栈构造结点入栈

计算表达式树：
若为叶子结点(左右子树均为空)，返回结点值
否则，取操作数和运算符进行计算

2.代码截图

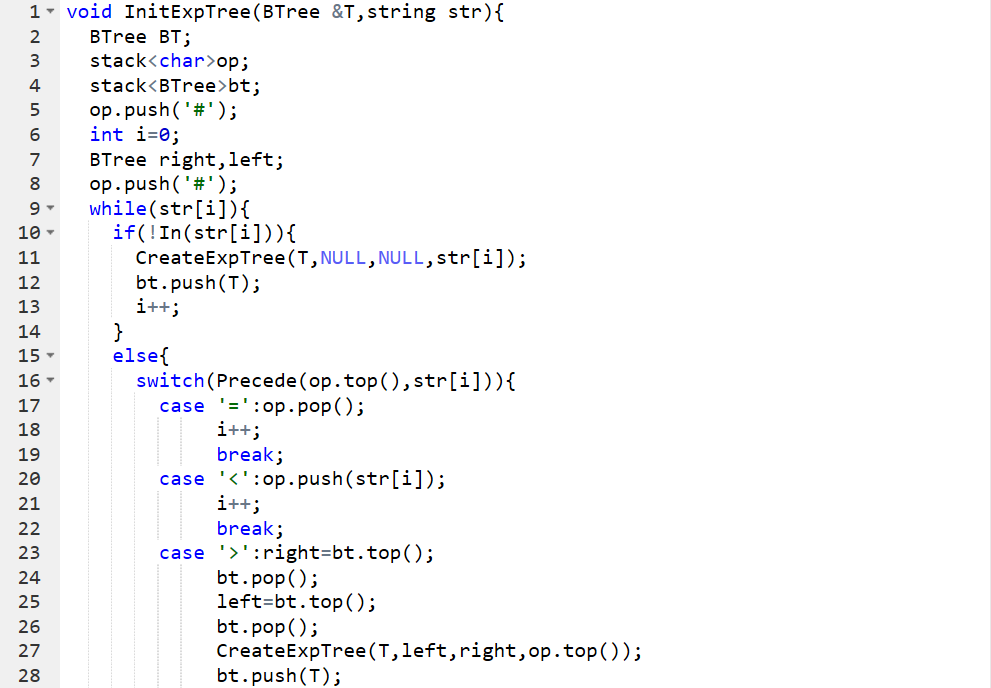
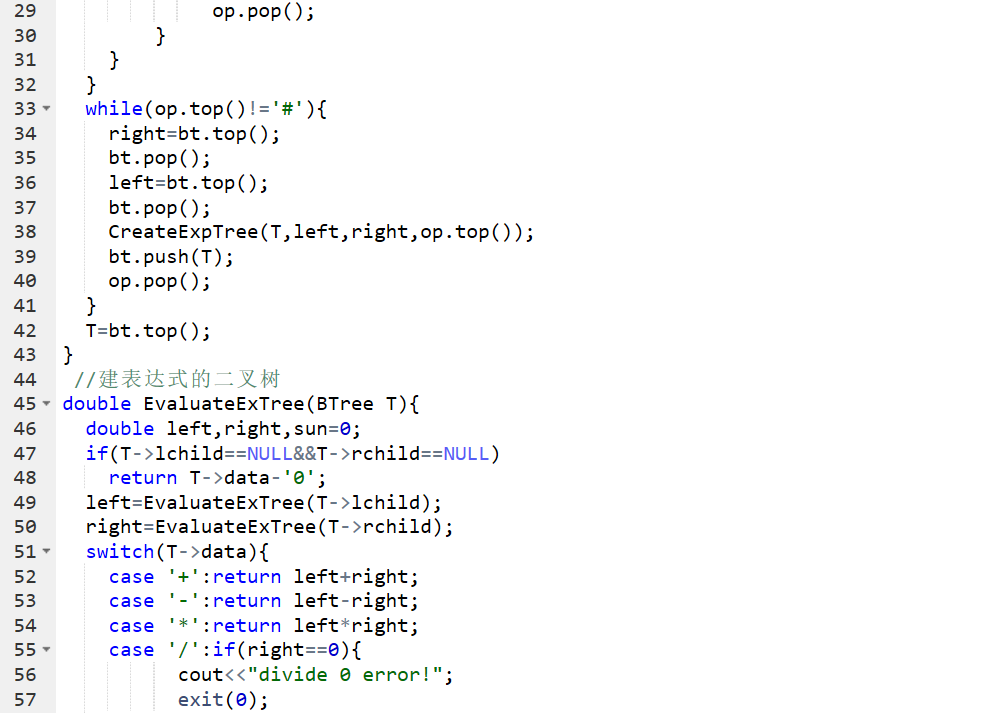
3. PTA提交列表说明。

答案错误：除0错误
原因：计算表达式树函数有返回值，遇到除数为0的情况
解决方法：将

case '/':if(right==0)
			cout<<"divide 0 error!";
	    else return left/right;
	}

改为

case '/':if(right==0){
			cout<<"divide 0 error!";
			exit(0);
		}
	    return left/right;
	}

题目3：7-7 修理牧场

1. 设计思路

定义a[n]存放长度，sum表示每次锯木头的费用，total表示总费用
将木块长度存入数组并按从小到大顺序排序
for i=0 to n-2
    sum=最小两项和
    total+=sum
    将sum插入数组，数组保持从小到大顺序
end for
输出总费用

2.代码截图

3. PTA提交列表说明。

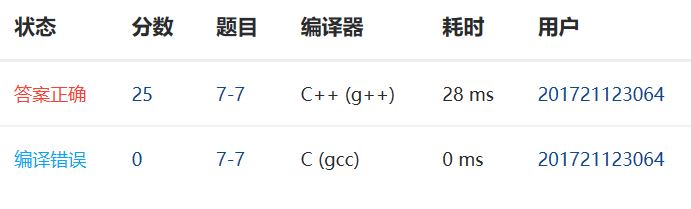
编译错误：使用C++头文件却用C编译器

3.截图本周题目集的PTA最后排名

3.1 PTA排名截图

3.2 我的总分：

1.5分

4. 阅读代码（必做）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 3;
struct node{
    int dad, mom;   
    char sex;       
    node(): dad(-1), mom(-1), sex('M'){} 
}fam[N];
bool Find(int a, int b, int cnt)
{
    if(a == -1 || b == -1) return true;
    if((fam[a].dad != -1 && fam[a].dad == fam[b].dad) || (fam[a].mom != -1 && fam[a].mom == fam[b].mom))
        return false;
    cnt++;
    if(cnt >= 4) return true;
    return(Find(fam[a].dad, fam[b].mom, cnt) && Find(fam[a].mom, fam[b].dad, cnt) && Find(fam[a].dad, fam[b].dad, cnt) && Find(fam[a].mom, fam[b].mom, cnt));
}
int main()
{
    int n, m, id;
    scanf("%d", &n);
    while(n--)
    {
        scanf("%d", &id);
        getchar();
        scanf("%c%d%d", &fam[id].sex, &fam[id].dad, &fam[id].mom);
        if(fam[id].dad != -1)
            fam[fam[id].dad].sex = 'M';
        if(fam[id].mom != -1)
            fam[fam[id].mom].sex = 'F';
    }
    scanf("%d", &m);
    int a, b;
    while(m--)
    {
        scanf("%d%d", &a, &b);
        if(fam[a].sex == fam[b].sex)
            printf("Never Mind\n");
        else
        {
            if(Find(a, b, 0))
                printf("Yes\n");
            else
                printf("No\n");
        }
    }
    return 0;
}

该代码功能：判断两个人最近的共同祖先是否五代以内，能否通婚
优点:利用递归遍历判断，代码简洁，可读性较强
代码相关地址:https://blog.csdn.net/jiang_1603/article/details/79731264

5. 代码Git提交记录截图