二叉树、前序遍历、中序遍历、后序遍历
一、树
在谈二叉树前先谈下树和图的概念
树:不包含回路的连通无向图(树是一种简单的非线性结构)
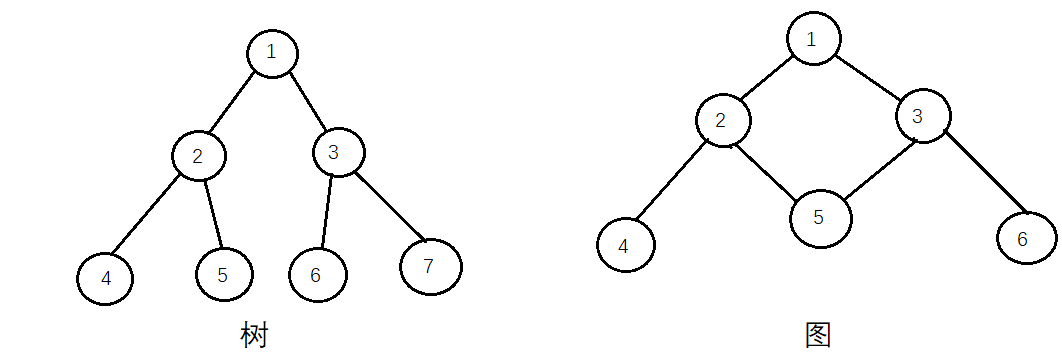
树有着不包含回路这个特点,所以树就被赋予了很多特性
1、一棵树中任意两个结点有且仅有唯一的一条路径连通
2、一棵树如果有n个结点,那它一定恰好有n-1条边
3、在一棵树中加一条边将会构成一个回路
4、树中有且仅有一个没有前驱的结点称为根结点
在对树进行讨论的时候将树中的每个点称为结点,
根结点:没有父结点的结点
叶结点:没有子结点的结点
内部结点:一个结点既不是根结点也不是叶结点
每个结点还有深度,比如上图左边的树的4号结点深度是3(深度是指从根结点到这个结点的层数,根结点为第一层)
二、二叉树
基本概念:
二叉树是一种非线性结构,二叉树是递归定义的,其结点有左右子树之分
二叉树的存储结构:
二叉树通常采用链式存储结构,存储结点由数据域和指针域(指针域:左指针域和右指针域)组成,二叉树的链式存储结构也称为二叉链表,对满二叉树和完全二叉树可按层次进行顺序存储
特点:
1、每个结点最多有两颗子树
2、左子树和右子树是有顺序的,次序不能颠倒
3、即使某结点只有一个子树,也要区分左右子树
4、二叉树可为空,空的二叉树没有结点,非空二叉树有且仅有一个根节点
二叉树中有两种特殊的二叉树:满二叉树、完全二叉树
满二叉树:二叉树中每个内部结点都有存在左子树和右子树(或者说满二叉树所有的叶结点都有同样的深度)
满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树
(满二叉树的严格的定义是:一颗深度为h且有2h-1个结点的二叉树)
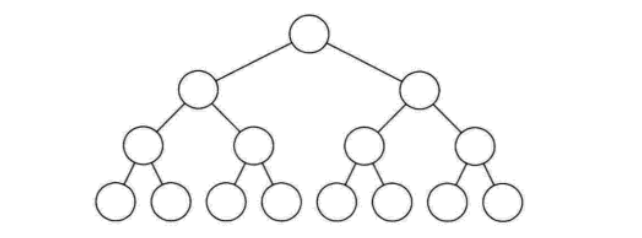
(图片来源:https://www.cnblogs.com/polly333/p/4740355.html)
完全二叉树:
第一种解释:如果一颗二叉树除最右边位置上有一个或几个叶结点缺少外,其他是丰满的那么这样的二叉树就是完全二叉树(这句话不太好理解),看下面第二种解释
第二种解释:除第h层外,其他各层(1到h-1)的结点数都达到最大个数,第h层从右向左连续缺若干结点,则这个二叉树就是完全二叉树
也就是说如果一个结点有右子结点,那么它一定也有左子结点
第三种解释:除最后一层外,每一层上的节点数均达到最大值,在最后一层上只缺少右边的若干结点
完全二叉树的形状类似于下图
为了方便理解请看下图(个人理解:完全二叉树就是从上往下填结点,从左往右填,填满了一层再填下一层)
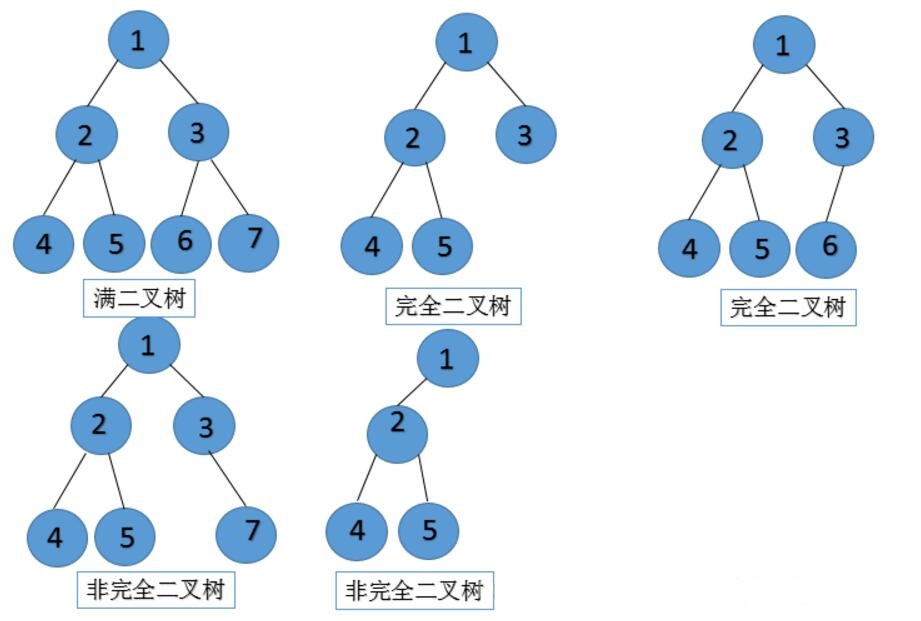
(图片来源:https://www.cnblogs.com/polly333/p/4740355.html#3)
二叉树相关词语解释:
结点的度:结点拥有的子树的数目
叶子结点:度为0的结点(tips:在任意一个二叉树中,度为0的叶子结点总是比度为2的结点多一个)
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
树的高度:树中结点的最大层次
二叉树基本性质:
性质1:在二叉树的第k层上至多有2k-1个结点(k>=1)
性质2:在深度为m的二叉树至多有2m-1个结点
性质3:对任意一颗二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个
性质4:具有n个结点的完全二叉树的深度至少为[log2n]+1,其中[log2n]表示log2n的整数部分
存储方式
存储的方式和图一样,有链表和数组两种,用数组存访问速度快,但插入、删除节点操作就比较费时了。实际中更多的是用链来表示二叉树(下面的实现代码使用的是链表)
实现代码:
1 #include <stdio.h>
2 #include <stdlib.h>
3 #define N 10
4
5 typedef struct node
6 {
7 char data;
8 struct node *lchild; /* 左子树 */
9 struct node *rchild; /* 右子树 */
10
11 }BiTNode, *BiTree;
12
13 void CreatBiTree (BiTree *T) /* BiTree *T等价于 struct node **T */
14 {
15 char ch;
16
17 scanf("%c", &ch);
18 if (ch == '#') /* 当遇到#时,令树的结点为NULL,从而结束该分支的递归 */
19 {
20 *T = NULL;
21 }
22 else
23 {
24 *T = (BiTree)malloc(sizeof(BiTNode));
25 if (*T == NULL)
26 {
27 printf("内存分配失败");
28 exit(0);
29 }
30 (*T)->data = ch; /* 生成结点 */
31 CreatBiTree(&(*T)->lchild); /* 构造左子树 */
32 CreatBiTree(&(*T)->rchild); /* 构造右子树 */
33 /* 这里需要注意的是->的优先级比&高,所以&(*T)->lchild得到的是lchild的地址 */
34 }
35
36 }
37 int main()
38 {
39 int level = 1;
40
41 BiTree t = NULL;
42 printf("以前序遍历方式输入二叉树\n");
43 CreatBiTree(&t); /* 传入指针的地址 */
44 }
上面的代码采用的是以前序遍历方式输入二叉树,当输入“#”时,指针指向NULL,说明是改结点是叶结点
三、二叉树的遍历(前序\中序\后序遍历)
二叉树的遍历是指不重复地访问二叉树中所有结点,主要指非空二叉树,对于空二叉树则结束返回,二叉树的遍历主要包括前序遍历、中序遍历、后序遍历
前序遍历:首先访问根结点,然后遍历左子树,最后遍历右子树(根->左->右)
顺序:访问根节点->前序遍历左子树->前序遍历右子树
1 /* 以递归方式 前序遍历二叉树 */
2 void PreOrderTraverse(BiTree t, int level)
3 {
4 if (t == NULL)
5 {
6 return ;
7 }
8 printf("data = %c level = %d\n ", t->data, level);
9 PreOrderTraverse(t->lchild, level + 1);
10 PreOrderTraverse(t->rchild, level + 1);
11 }
中序遍历:首先遍历左子树,然后访问根节点,最后遍历右子树(左->根->右)
顺序:中序遍历左子树->访问根节点->中序遍历右子树
1 /* 以递归方式 中序遍历二叉树 */
2 void PreOrderTraverse(BiTree t, int level)
3 {
4 if (t == NULL)
5 {
6 return ;
7 }
8 PreOrderTraverse(t->lchild, level + 1);
9 printf("data = %c level = %d\n ", t->data, level);
10 PreOrderTraverse(t->rchild, level + 1);
11 }
后序遍历:首先遍历左子树,然后遍历右子树,最后访问根节点(左->右->根)
顺序:后序遍历左子树->后序遍历右子树->访问根节点
1 /* 以递归方式 后序遍历二叉树 */
2 void PreOrderTraverse(BiTree t, int level)
3 {
4 if (t == NULL)
5 {
6 return ;
7 }
8 PreOrderTraverse(t->lchild, level + 1);
9 PreOrderTraverse(t->rchild, level + 1);
10 printf("data = %c level = %d\n ", t->data, level);
11 }
从上面可以看出,三种遍历方式极其相似,只是语句 printf("data = %c level = %d\n ", t->data, level);的位置发生了变化


 浙公网安备 33010602011771号
浙公网安备 33010602011771号