洛谷P4016 负载平衡问题（费用流）

题目

https://www.luogu.com.cn/problem/P4016

思路

这题是网络流24题中的一道相对简单的题。既然是网络流题，我们先考虑怎么建图。

读入各仓库货物数\(a[i]\)求出平均值\(\frac{sum}{n}\)，我们就知道每一个仓库需要调入/调出多少货物，令\(f(i)=a[i]-\frac{sum}{n}\)。

新建一个源点S和一个汇点T，对于任意的\(i\)，若\(f(i)>0\)，说明该仓库要向其他仓库调出货物，我们加入一条从S到\(i\)的边，边权为0，容量为\(f(i)\)。可以看成本来没有东西，源点S通过这条边给了它\(f(i)\)个。它必须要把这\(f(i)\)个流走。

同理，若\(f(i)<0\)，说明该仓库要从其他仓库调入货物，我们加入一条从\(i\)到T的边，边权为0，容量为\(-f(i)\)。可以看成本来是负的，只有满足了这条边，才说明有其他仓库流向它将其补为0。

至于环内的边，没有限制，随便流，一定是满足负载平衡的。将每一个点与其相邻点连边，边权为1，容量为无穷。

图片可以帮助理解：

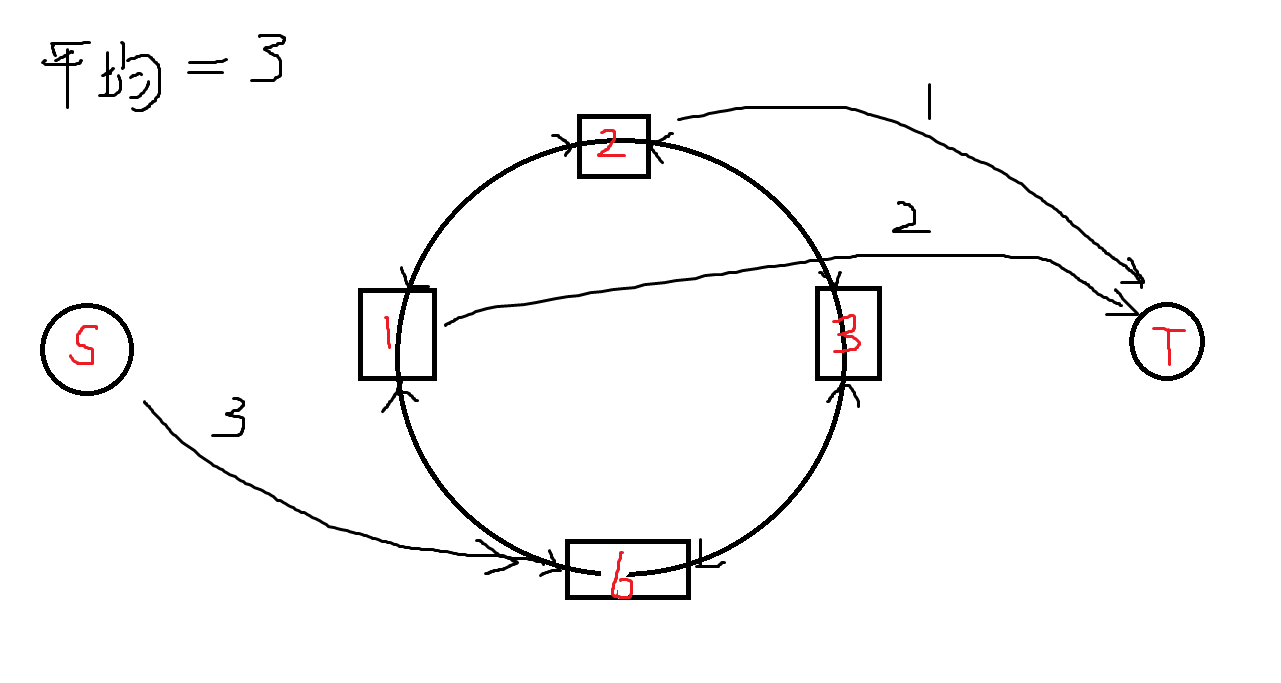
跑一遍最小费用最大流就ok了。图片只是示例，写代码的时候不要忘记处理反向边。

代码

#include<cstdio>
#include<cstdlib>
#include<queue>
#include<cstring>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;
int n,fst[110],nxt[1000],cnt=0,a[101],book[110],dis[110],pre[110];
struct edge{
    int u,v,w,cap;
} e[1000];
void add(int x,int y,int z,int k){
    e[++cnt].u=x;
    e[cnt].v=y;
    e[cnt].w=z;
    e[cnt].cap=k;
    nxt[cnt]=fst[x];
    fst[x]=cnt;
}
int spfa(){
    int i;
    queue<int> q;
    memset(book,0,sizeof(book));
    memset(dis,inf,sizeof(dis));
    dis[0]=0;book[0]=1;
    q.push(0);
    while(!q.empty()){
        int p=q.front();
        for(i=fst[p];i;i=nxt[i]){
            if(e[i].cap<=0) continue;
            if(dis[e[i].v]>dis[p]+e[i].w){
                dis[e[i].v]=dis[p]+e[i].w;
                pre[e[i].v]=i;
                if(!book[e[i].v]){
                    book[e[i].v]=1;
                    q.push(e[i].v);
                }
            }
        }
        book[p]=0;
        q.pop();
    }
    if(dis[n+1]<inf) return 1;
    else return 0;
}
int inv(int x){
    if(x&1) return x+1;
    else return x-1;
}
int dinic(){
    int i,ans=0;
    while(spfa()){
        int flow=inf;
        for(i=n+1;i;i=e[pre[i]].u)
            flow=min(e[pre[i]].cap,flow);
        for(i=n+1;i;i=e[pre[i]].u){
            e[pre[i]].cap-=flow;
            e[inv(pre[i])].cap+=flow;
        }
        ans+=flow*dis[n+1];
    }
    return ans;
}
int main(){
    int i,j,x,sum=0,ans;
    scanf("%d",&n);
    for(i=1;i<=n;i++){
        scanf("%d",&a[i]);
        sum+=a[i];
    }
    for(i=1;i<=n;i++){
        x=a[i]-sum/n;
        if(x<0){
            add(i,n+1,0,-x);
            add(n+1,i,0,0);
        }
        if(x>0){
            add(0,i,0,x);
            add(i,0,0,0);
        }
    }
    for(i=1;i<=n;i++){
        add(i,i%n+1,1,inf);
        add(i%n+1,i,-1,0);
        add(i,(i-2+n)%n+1,1,inf);
        add((i-2+n)%n+1,i,-1,0);
    }
    printf("%d",dinic());
    system("pause");
    return 0;
}