洛谷P1260 工程规划

题目链接

https://www.luogu.com.cn/problem/P1260

思路

这是一道差分约束模板题。什么是差分约束？简单来说就是一组\(n\)元一次不等式组，每个不等式以\(x_i-x_j\leq k\)的形式给出，求化简之后各个变量之间的关系。

可以看成图论问题，如果\(x_i-x_j\leq k\)，我们就建一条从\(x_j\)到\(x_i\)(注意顺序！！)，边权为\(k\)的边，表示\(x_j\)到\(x_i\)的距离\(\leq k\)，

钦定一个源点，那么对任意\(x_i\)，\(x_i\)需要满足从源点到\(x_i\)的路径代表的所有不等式，所以\(x_i\)的最大值就是源点到\(x_i\)的最短路（各个解集求交集，\(x_i\leq\)最短路）。

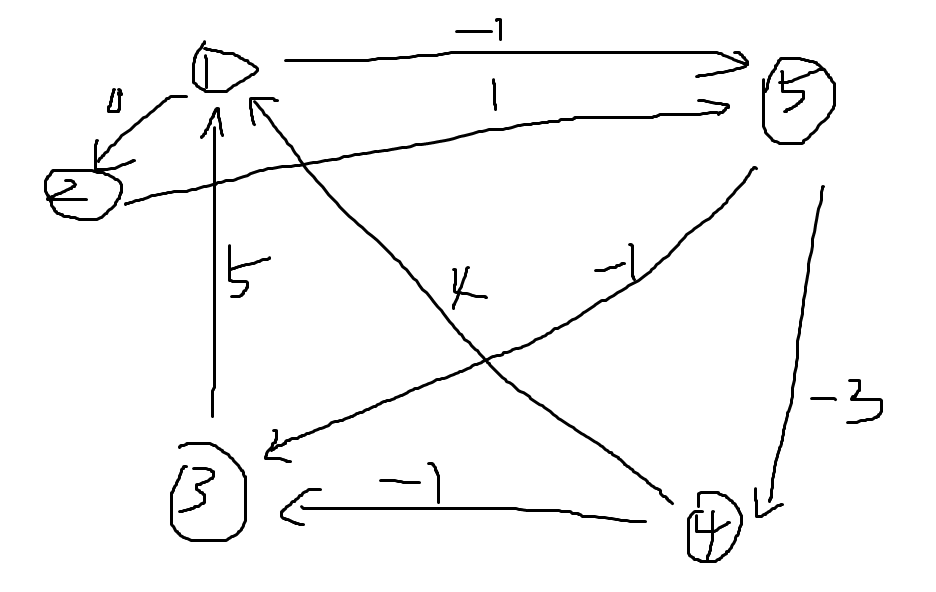
比如：\(\left\{\begin{array}\\x_5-x_1\leq -1\\{x_2-x_1<=0}\\x_5-x_2\leq 1 \end{array}\right.\)
联立解得\(x_5-x_1\leq -1\)，就是\(x_1\)到\(x_5\)的最短路。

注意有负权边，如果有负环的话该不等式组无解（相当于套圈之后\(x_i\leq x_i-C\)(C是某常数)），体现在spfa中就是某节点入队次数大于总点数。

但是这是针对连通图而言，如果图不连通，有的节点根本无法访问到，那就建一个超级源S，加入S到1至n号节点的n条边，边权为0。

代码

#include<cstdio>
#include<cstdlib>
#include<queue>
#define db double
#define inf 0x3f3f3f3f
#define maxn (int)(1e4+10)
using namespace std;
int fst[maxn],nxt[maxn],w[maxn],to[maxn],cnt=0,dis[maxn],n,m;
int book[maxn],flag=0,num[maxn];
void add(int x,int y,int z){
	w[++cnt]=z;
	to[cnt]=y;
	nxt[cnt]=fst[x];
	fst[x]=cnt;
}
bool spfa(){
	int i;
	queue<int> q;
	while(!q.empty()) q.pop();
	for(i=1;i<=n;++i)
		dis[i]=inf;
	q.push(n+1);
	book[n+1]=1;
	while(!q.empty()){
		int p=q.front();
		for(i=fst[p];i;i=nxt[i]){
			if(dis[p]+w[i]<dis[to[i]]){
				dis[to[i]]=dis[p]+w[i];
				if(!book[to[i]]){
					num[to[i]]++;
					if(num[to[i]]>n+1) return 0;
					q.push(to[i]);
					book[to[i]]=1;
				}
			}
		}
		book[p]=0;
		q.pop();
	}
	return 1;
}
int main(){
	int i,x,y,z,MIN=inf;
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;++i){
		scanf("%d%d%d",&x,&y,&z);
		add(y,x,z);
	}
	for(i=1;i<=n;i++){
		add(n+1,i,0);
	}
	if(spfa()){
		for(i=1;i<=n;i++)
			MIN=min(MIN,dis[i]);
		for(i=1;i<=n;i++)
			printf("%d\n",dis[i]-MIN);
	}
	else printf("NO SOLUTION");
	// system("pause");
	return 0;
}