python常用算法
常用排序算法
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括:
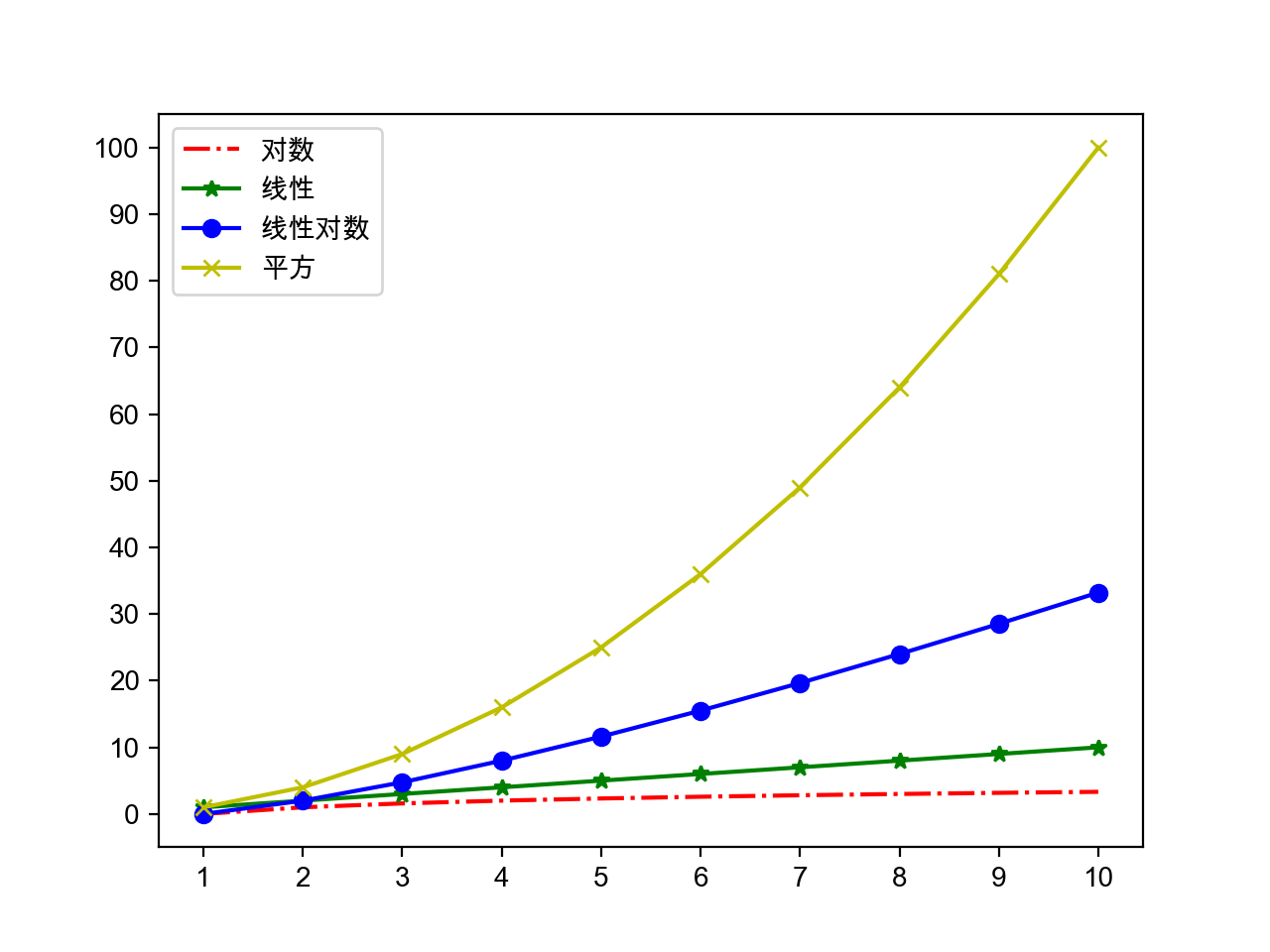
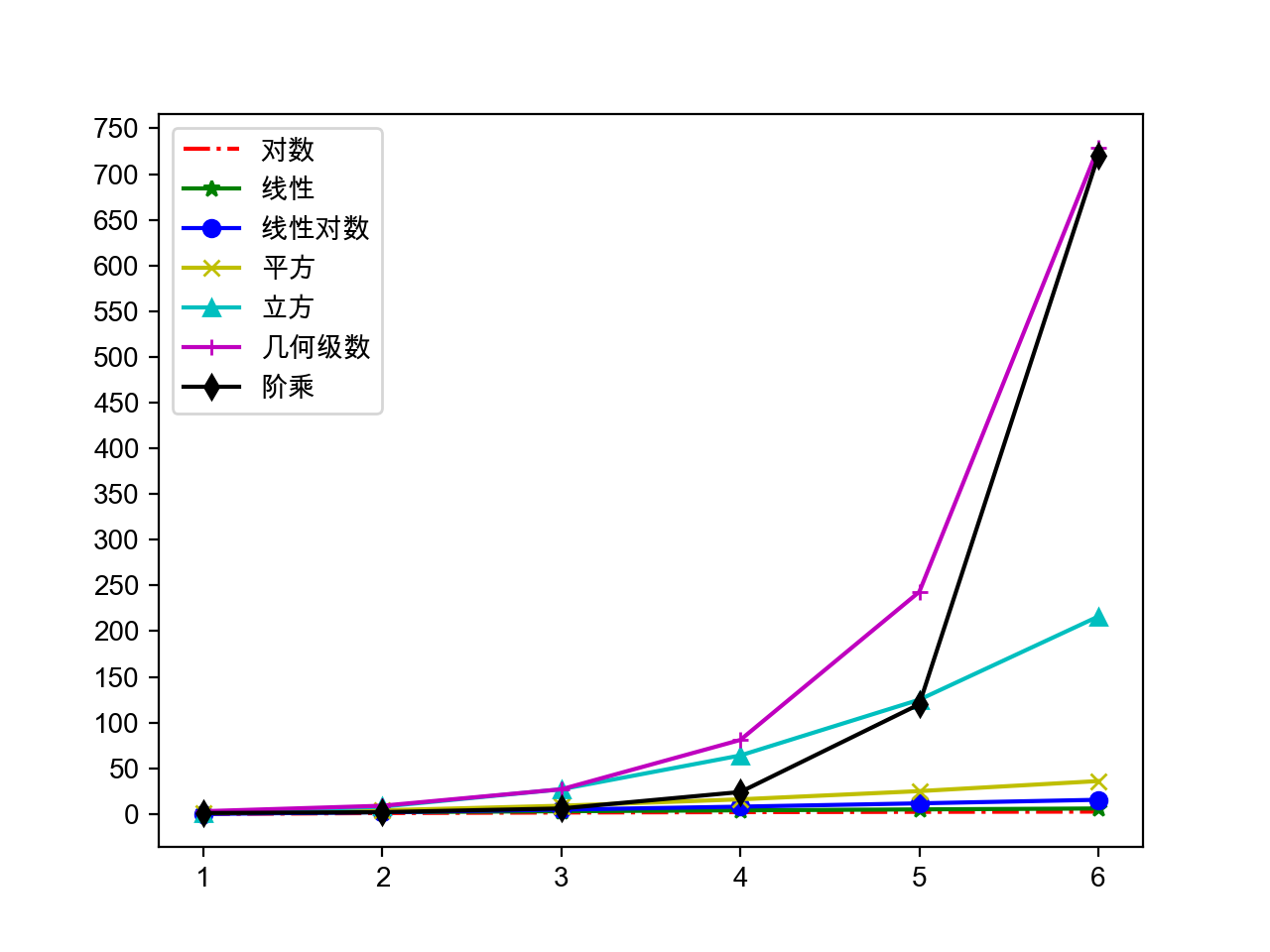
- 稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同
- 排序方式:In-place:占用常数内存,不占用额外内存;Out-place:占用额外内存
- n:数据规模
1. 冒泡排序
- 效率:O(n2)
- 原理:
- 1.每一趟比较相邻的元素,如果逆序(前大后小),就交换他们两个;每一趟都把大的元素往后调。
- n个元素最多n-1趟排序

def bubble_sort1(origin_items,comp=lambda x, y: x > y):
items = origin_items[:]
for i in range(len(items) - 1):
for j in range(i, len(items) - 1 - i):
if comp(items[j], items[j + 1]):
items[j], items[j + 1] = items[j + 1], items[j]
# 改进1
def bubble_sort1(origin_items,comp=lambda x, y: x > y):
items = origin_items[:]
for i in range(len(items) - 1):
swapped = False # 交换标志
for j in range(i, len(items) - 1 - i):
if comp(items[j], items[j + 1]):
items[j], items[j + 1] = items[j + 1], items[j]
if not swapped: # 如果一趟排序中没有交换,则说明整体有序,结束排序
break
# 改进版2
def bubble_sort2(origin_items, comp=lambda x, y: x > y):
"""高质量冒泡排序(搅拌排序)"""
items = origin_items[:]
for i in range(len(items) - 1):
swapped = False
for j in range(i, len(items) - 1 - i): # 从左向右排序
if comp(items[j], items[j + 1]):
items[j], items[j + 1] = items[j + 1], items[j]
swapped = True
if swapped:
swapped = False
for j in range(len(items) - 2 - i, i, -1): # 从右向左排序
if comp(items[j - 1], items[j]):
items[j], items[j - 1] = items[j - 1], items[j]
swapped = True
if not swapped:
break
return items
2. 选择排序
- 效率:O(n2)
- 原理:从头至尾扫描序列,找出最小的一个元素,和第一个元素交换,接着从剩下的元素中继续这种选择和交换方式,最终得到一个有序序列。
def select_sort(origin_items, comp=lambda x, y: x < y):
"""简单选择排序"""
items = origin_items[:]
for i in range(len(items) - 1):
min_index = i
for j in range(i + 1, len(items)):
if comp(items[j], items[min_index]):
min_index = j
items[i], items[min_index] = items[min_index], items[i]
return items
3. 插入排序
- 效率:
- 原理
- 将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
- 从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
def insertionSort(arr):
for i in range(len(arr)):
preIndex = i-1
current = arr[i]
while preIndex >= 0 and arr[preIndex] > current:
arr[preIndex+1] = arr[preIndex]
preIndex-=1
arr[preIndex+1] = current
return arr
4. 归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
- 自下而上的迭代;
分治法:
- 分割:递归地把当前序列平均分割成两半。
- 集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
def merge_sort(items, comp=lambda x, y: x <= y):
"""归并排序(分治法)"""
if len(items) < 2:
return items[:]
mid = len(items) // 2
left = merge_sort(items[:mid], comp)
right = merge_sort(items[mid:], comp)
return merge(left, right, comp)
def merge(items1, items2, comp):
"""合并(将两个有序的列表合并成一个有序的列表)"""
items = []
index1, index2 = 0, 0
while index1 < len(items1) and index2 < len(items2):
if comp(items1[index1], items2[index2]):
items.append(items1[index1])
index1 += 1
else:
items.append(items2[index2])
index2 += 1
items += items1[index1:]
items += items2[index2:]
return items
5. 快速排序
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为较小和较大的2个子序列,然后递归地排序两个子序列。步骤为:
- 挑选基准值:从数列中挑出一个元素,称为"基准"(pivot);
- 分割:重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(与基准值相等的数可以到任何一边)。在这个分割结束之后,对基准值的排序就已经完成;
- 递归排序子序列:递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。
# 快速排序 - 选择枢轴对元素进行划分,左边都比枢轴小右边都比枢轴大
def quick_sort(origin_items, comp=lambda x, y: x <= y):
items = origin_items[:]
_quick_sort(items, 0, len(items) - 1, comp)
return items
def _quick_sort(items, start, end, comp):
if start < end:
pos = _partition(items, start, end, comp)
_quick_sort(items, start, pos - 1, comp)
_quick_sort(items, pos + 1, end, comp)
def _partition(items, start, end, comp):
pivot = items[end]
i = start - 1
for j in range(start, end):
if comp(items[j], pivot):
i += 1
items[i], items[j] = items[j], items[i]
items[i + 1], items[end] = items[end], items[i + 1]
return i + 1



 浙公网安备 33010602011771号
浙公网安备 33010602011771号