看机器学习看到了回归函数,看了一半看不下去了,看到能用方差进行函数回归,又手痒痒了,自己推公式写代码验证:
常见的最小二乘法是一阶函数回归
回归方法就是寻找方差的最小值
y = kx + b
xi, yi
y-yi = kxi+b-yi
方差为
∑(kxi + b - yi )^2
f = k^2∑xi^2 + b^2 + ∑yi^2 +2kb∑xi - 2k∑xi*yi - 2yib
求极值需要对其求微分,因为是二元函数,因此使用全微分公式,其极值点应该在两个元的偏微分都为0处
δf/δk = 2k∑(xi^2)+2(∑xib-∑xi*yi) = 0
δf/δb = 2b +2(k∑xi -∑yi) = 0
b = ∑yi - k∑xi
2k∑(xi^2) + 2(∑xi∑yi - k(∑xi)^2-∑xi*yi)
k = (∑xi*yi - ∑xi∑yi)/(∑(xi^2)-(∑xi)^2)
以上就是最小二乘法的推导
那么扩展到二阶函数拟合回归
y = c0+c1*x+c2*x^2
xi, yi
y - yi = c0 + c1*xi + c2*xi^2 - yi
c0^2 + c1^2∑xi^2 + c2^2∑xi^4 +yi^2...
其三元偏微分表示如下
0 = c0 + c1∑xi + c2∑xi^2 - ∑yi
0 = c1∑xi^2 + c0∑xi + c2∑xi^3 - ∑xi*yi
0 = c2∑xi^4 + c0∑xi^2 + c1∑xi^3 - ∑xi^2 * yi
解方程可以求出三个参数
更高阶的回归可就不能手解方程了,需要用线性代数的知识
y = c0 + c1 * x + c2 * x^2 + c3 * x^3
0 = c0 + c1∑xi +c2∑xi^2 + c3∑xi^3 - ∑yi
0 = c0∑xi + c1∑xi^2 + c2∑xi^3 +c3∑xi^4 - ∑xi*yi
0 = c0∑xi^2 + c1∑xi^3 + c2∑xi^4 + c3∑xi^5 - ∑xi^2*yi
0 = c0∑xi^3 + c1∑xi^4 +c2∑xi^5 +c3∑xi^6 - ∑xi^3*yi
M * [c0, c1, c2, c3]T = [∑yi, ∑xi*yi, ∑xi^2*yi, ∑xi^3*yi]T
[c0, c1, c2, c3]T = M^-1 * [∑yi, ∑xi*yi, ∑xi^2*yi, ∑xi^3*yi]T
实际上这个最终转为了求矩阵逆的过程
因此多阶函数的拟合回归本质是矩阵求逆,这对于应用数学工具而言是比较容易的
更普遍的,对于y = ∑cj*gj(x)的形式,有
Yj = ∑(i)(gj(xi) * yi)
Mj,k = ∑(i)(gj(xi) * gk(xi))
M * C = Y; C = M^(-1) * Y (M 为矩阵,C和Y为向量)
求解Ck可以得到线性参数集
数学最优美的地方就是可以化繁为简,而同样优美的是代码,使用python写出以上过程的算法验证
以下程序基于numpy和matplotlib,其实简单应用用python确实足以替代matlab了
为了防止高次计算溢出,对x, y进行归一,之前没做这步,算到四次回归就溢出了
x' = x/xmax
y' = y/ymax
y = ∑(Cj * gj(x / xmax))*ymax
对:
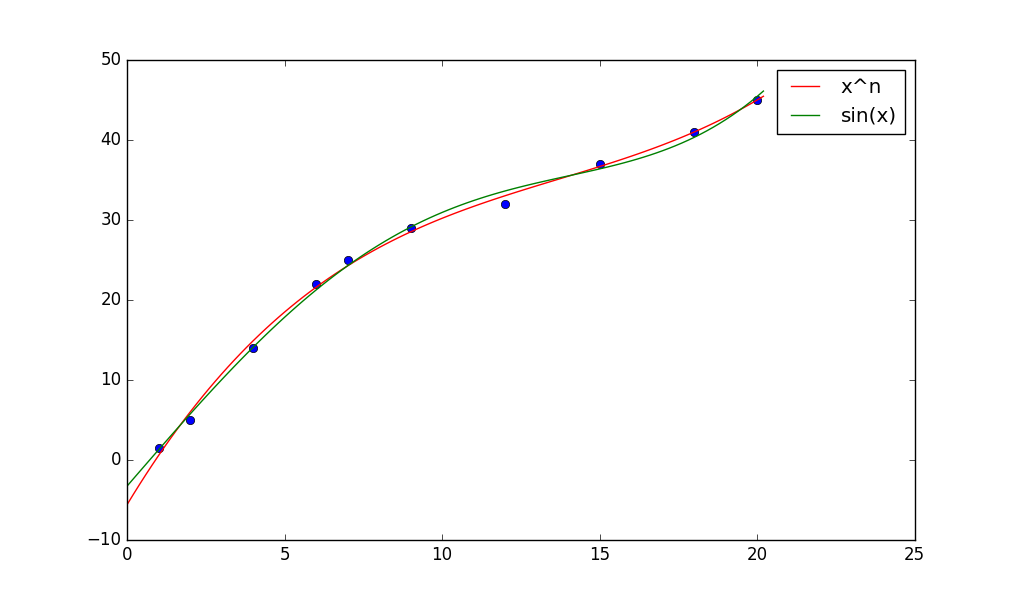
x = 1, 2, 4, 6, 7, 9, 12, 15, 18, 20
y = 1.5, 5, 14, 22, 25, 29, 32, 37, 41, 45
进行3阶函数回归计算,完整代码如下,为了强制符合PEP8规范,英文注释写的很蹩脚...
终于上代码了:
"""
name: regression
author: robocky
create time: 2017-1-1
description: Use polynomial function to fitting data
"""
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt
def polynomial(c: np.array, x: np.array, gs: list):
"""y = c0 * g0(x) + c1 * g1(x) + c2 * g2(x)...+ cn * gn(x)"""
return c.dot(np.array([g(x) for g in gs]))
def regression(x: np.array, y: np.array, gs: list):
"""Use inv of matrix to calculate regression
y = ∑ci * gi(x)
"""
y_res = np.array([sum(g(x) * y) for g in gs])
x_matrix = np.array([[sum(g(x) * h(x)) for g in gs] for h in gs])
return inv(x_matrix).dot(y_res)
def func_gen(n):
"""Generate power functions"""
return lambda x: x ** n
def func_gen_sin(n):
"""Generate sin functions"""
return (lambda x: x ** 0) if n == 0 else lambda x: np.sin(n * x)
if __name__ == '__main__':
# Test
x_list = np.array([1, 2, 4, 6, 7, 9, 12, 15, 18, 20])
y_list = np.array([1.5, 5, 14, 22, 25, 29, 32, 37, 41, 45])
g_list = [func_gen(i) for i in range(4)]
g_list2 = [func_gen_sin(i) for i in range(4)]
# Set numbers to unit, in order to avoid overflow
x_max, y_max = max(x_list), max(y_list)
c_list = regression(x_list / x_max, y_list / y_max, g_list)
c_list2 = regression(x_list / x_max, y_list / y_max, g_list2)
# plot
plt.figure()
plt.plot(x_list, y_list, 'bo')
x_line = np.arange(0, 1.02, 0.01)
plt.plot(x_line * x_max, polynomial(c_list, x_line, g_list) * y_max, color='red', label='x^n')
plt.plot(x_line * x_max, polynomial(c_list2, x_line, g_list2) * y_max, color='green', label='sin(x)')
plt.legend()
plt.show()
回归算法只有三行,当然计算过程都省略了,多项式也很简单
做了个函数生成器,理论上可以用任何函数进行回归运算,不过结果可能会发散,比如纯正弦函数,但加个常数项结果就收敛了
最后上个结果图