标题:方格分割
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
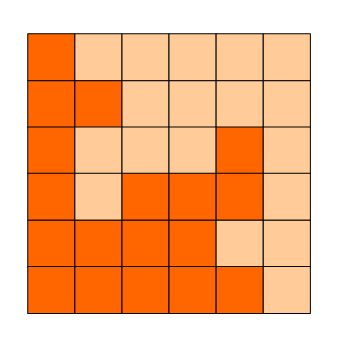
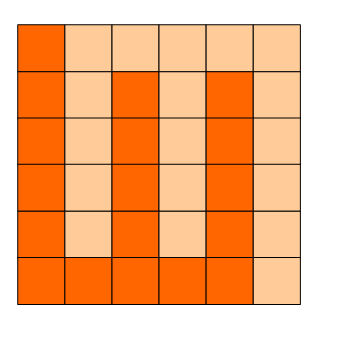
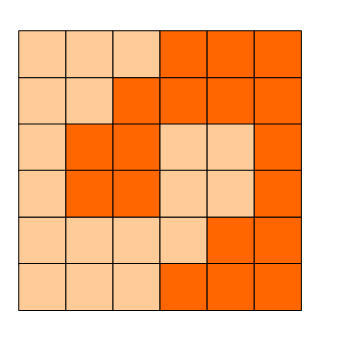
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
一开始想的是按着一个方块一个方块搜索,但是没有考虑到dfs只能是一笔画!!!所以样例的所有情况都没考虑到下面是我比赛的时候写的代码(知道结果的时候还是比较伤心的,花了大把的时间最后还是入坑了 哎 还是有待锻炼啊~~!!!):
<↓↓↓这个代码是错的哦!!!只是本人比赛时写的~~可以略过>
1 #include<stdio.h> 2 #include<math.h> 3 #include<ctype.h> 4 #include<string.h> 5 #include<stdlib.h> 6 7 int aa[4][2]={{0,1},{1,0},{0,-1},{-1,0}}; 8 int line[10][10]; 9 struct data { 10 int dis[6][6]; 11 }vis[10000]; 12 int sum; 13 void dfs(int x,int y,int n) 14 { 15 n++; 16 int i,j; 17 if(n>=18){ 18 for(i=0;i<6;i++){ 19 for(j=0;j<6;j++){ 20 vis[sum].dis[i][j]=line[i][j]; 21 //printf("%d ",line[i][j]); 22 } 23 //printf("\n"); 24 } 25 //system("pause"); 26 sum++; 27 return ; 28 } 29 int a,b; 30 for(i=0;i<4;i++){ 31 a=x+aa[i][0]; 32 b=y+aa[i][1]; 33 if(a>=0&&a<6&&b>=0&&b<6&&line[a][b]==-1){ 34 line[a][b]=1; 35 line[5-a][5-b]=0; 36 dfs(a,b,n); 37 line[a][b]=-1; 38 line[5-a][5-b]=-1; 39 } 40 } 41 return ; 42 } 43 int main () 44 { 45 memset(line,-1,sizeof(line)); 46 sum=0; 47 line[0][0]=1; 48 line[5][5]=0; 49 dfs(0,0,0); 50 int i,j,k,l,num=0; 51 for(i=0;i<sum;i++){ 52 int yy=0; 53 for(j=i+1;j<sum;j++){ 54 int y=1; 55 for(k=0;k<6;k++){ 56 for(l=0;l<6;l++){ 57 if(vis[i].dis[k][l]!=vis[j].dis[k][l]){ 58 y=0; 59 break; 60 } 61 } 62 if(y==0) 63 break; 64 } 65 if(y==1){ 66 yy=1; 67 break; 68 } 69 } 70 if(yy==0){ 71 for(k=0;k<6;k++){ 72 for(l=0;l<6;l++){ 73 printf("%d ",vis[i].dis[k][l]); 74 } 75 printf("\n"); 76 } 77 system("pause"); 78 num++; 79 } 80 } 81 printf("%d %d %d\n",sum,num,num/2);//sum为所有搜到的结果,num是去重之后的结果,因为num里面还没有考虑到左下和右上对称的情况,所以最后结果应对二取商 82 return 0; 83 }//最后结果是:45
后来在网上看到一个大牛写的解题报告,思路主要就是搜索他的切割线,把他的每种情况的切割线搜出来,虽然方块不是一笔画,但是他的切割线肯定是一个一笔画啊(一刀两快儿
),而且每一种切割线都会经过中间的那个点(肯定啊!!(3,3)和(4,4)肯定不在同一个块儿里面啊~~~所以切割线肯定会经过他们相邻的那个点),切割线应该从中点开始搜索,而且只要搜索到边线(就是已经把方块分成两部分了)就可以结束,从中点开始搜第一步有四个方向,而且任意一个方向反转一下都可以得到另一个方向的所有情况,所以使用边线搜索的结果最后应该除以/4,下面是从网上搜到的代码:出自http://blog.csdn.net/y1196645376/article/details/69718192/
1 #include <algorithm> 2 #include <string.h> 3 #include <iostream> 4 #include <stdio.h> 5 #include <string> 6 #include <vector> 7 #include <queue> 8 #include <map> 9 #include <set> 10 using namespace std; 11 const int N = 6; 12 int ans = 0; 13 int mpt[N+1][N+1]; 14 int dir[4][2] = {0,1,1,0,0,-1,-1,0}; 15 void dfs(int x,int y) 16 { 17 if(x == 0 || y == 0 || x == N || y == N){ 18 int i,j; 19 ans ++; 20 return; 21 } 22 for(int i = 0 ; i < 4 ; i ++) 23 { 24 int tx = x + dir[i][0]; 25 int ty = y + dir[i][1]; 26 if(mpt[tx][ty])continue; 27 mpt[tx][ty] = 1; 28 mpt[N-tx][N-ty] = 1; 29 dfs(tx,ty); 30 mpt[tx][ty] = 0; 31 mpt[N-tx][N-ty] = 0; 32 } 33 } 34 int main() 35 { 36 mpt[N/2][N/2] = 1; 37 dfs(N/2,N/2); 38 printf("%d\n",ans/4); 39 return 0; 40 }最后结果 509
但是看到这个代码之后呢,感觉还是有点问题,从中点开始搜索,有四个方向,最后结果除以四,但是在每一个方向里面也会有一些对称的啊例如下图啊假设一开始的时候从中心的点往右走,就可以得到这两种一不同的分割线(所以感觉还是有问题的,有待更新吧,也许是我考虑的东西多了吧):




 posted on
posted on

