hdu 1253 胜利大逃亡 (代码详解)解题报告

胜利大逃亡

Problem Description

Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.

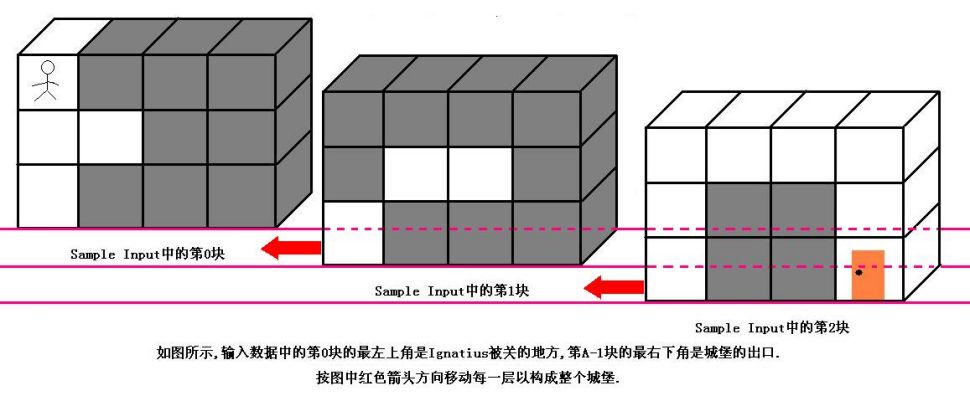
魔王住在一个城堡里,城堡是一个A*B*C的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.

 

Input

输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)

特别注意:本题的测试数据非常大,请使用scanf输入,我不能保证使用cin能不超时.在本OJ上请使用Visual C++提交.

 

Output

对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.

 

Sample Input

1 3 3 4 20 0 1 1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 1 1 0 0 1 1 0

 

Sample Output

11

 

题意：相当于给一个立方体，立方体的一个定点（1，1，1）找到另一个定点（a,b,c）,需要注意的是题目中（红颜色的）特别提醒，感觉这个题要是使用深搜的话会超时，所以这个是一个广搜，而且还是一个三维的广搜（其实三维的广搜和二位的没有什么区别，二位的是两个变量，三维的是三个变量罢了）。具体思路就是按照二位的广搜的思路来进行。

代码如下：

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<ctype.h>
#include<queue>
#include<stdlib.h>
#include<algorithm>
using namespace std;

int map[55][55][55];
int vis[55][55][55];		//vis用来标记
typedef struct{
    int z,x,y;
}node;
int aa[6][3]={1,0,0, -1,0,0, 0,0,1, 0,1,0, 0,0,-1, 0,-1,0}; 	//根据三维坐标轴，一共有六个方向
int a,b,c,tt,yy;
void bfs()
{
    node w,d;
    w.z=1;
    w.x=1;
    w.y=1;
    queue <node > q;
    q.push( w);
    while(!q.empty()){		//广搜
        d=q.front();
        for(int i=0;i<6;i++){
            w.z=d.z+aa[i][0];
            w.x=d.x+aa[i][1];
            w.y=d.y+aa[i][2];
            if(w.z>=1&&w.z<=a&&w.x>=1&&w.x<=b&&w.y>=1&&w.y<=c &&map[w.z][w.x][w.y]==0&&vis[w.z][w.x][w.y]==0){
                vis[w.z][w.x][w.y]=vis[d.z][d.x][d.y]+1;
                if(vis[w.z][w.x][w.y]>tt)		//为了防止超时进行适当的剪枝
                	return ;
                if(w.z==a&&w.x==b&&w.y==c){
                	yy=1;
                    printf("%d\n",vis[d.z][d.x][d.y]);
                    return ;
                }else {
                    q.push(w);
                }
            }
        }
        q.pop();
    }
    return ;
}
int main ()
{
    int t;
    int i,j,k;
    scanf("%d",&t);
    while(t--){
        scanf("%d %d %d %d",&a,&b,&c,&tt);
        memset(vis,0,sizeof(vis));
        for(i=1;i<=a;i++){
            for(j=1;j<=b;j++){
                for(k=1;k<=c;k++){
                    scanf("%d",&map[i][j][k]);
                }
            }
        }
        yy=0;
	vis[1][1][1]=1;
	bfs();
	if(yy==0){
            	printf("-1\n");
	}
    }
    return 0;
}