并查集(详)
作用:
判断两个点是否属于同一个集合
引入:
题意大致如下:输入n表示有n个人,m对x,y表示x,y在同一集合里,k对询问表示查询x,y是否在同一集合
这个问题的核心在于如何判断x,y在同一集合
其中一种暴力做法是,
使用数组fa[ ]表示:点x隶属于fa[x]所隶属的集合
初始化:
那么毫无疑问,初始化即为
for(int i=1;i<=n;++i) fa[i]=i;
因为最开始自己是只隶属于自己的集合
updata:
for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); while(u!=fa[u]) u=fa[u]; //寻找目前u的集合的集合头 while(v!=fa[v]) v=fa[v]; //寻找目前v的集合的集合头 fa[u]=v; //u的集合被合并到v的集合中,即u的集合的集合头变为v的集合的集合头 }
按照如上的代码可以使每个集合拥有两个性质:
1.该个集合中总有一个点x可以使fa[x]=x,暂且x称为"集合头",每个集合的集合头都不同
2.不论从那个点用fa[ ]值进行递归,总可以找到x即集合头
我们就可以顺利地用集合头代表这个集合
由于题目只查询两者是否属于同一集合,所以其中fa[u]=v等效于fa[v]=u,都是把两个集合合并成一个集合,所以实质上集合的合并等同于集合头的合并。
query:
只要判定两点的集合头是否相同,若相同则是同一个集合
for(int i=1;i<=k;++i){ int u,v; scanf("%d%d",&u,&v); while(u!=fa[u]) u=fa[u]; while(v!=fa[v]) v=fa[v]; if(u==v) printf("Yes\n"); else printf("No\n"); }
贴:
所以放一下暴力代码,暴力仍然可以水过这题.....
#include<bits/stdc++.h> #define maxn 1000010 using namespace std; int n,m,k,fa[maxn]; int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); while(u!=fa[u]) u=fa[u]; while(v!=fa[v]) v=fa[v]; fa[u]=v; } for(int i=1;i<=k;++i){ int u,v; scanf("%d%d",&u,&v); while(u!=fa[u]) u=fa[u]; while(v!=fa[v]) v=fa[v]; if(u==v) printf("Yes\n"); else printf("No\n"); } return 0; }
优化:
我们可以发现大量的时间用在了递归寻找集合点的过程上
如果在每次寻找的过程中把集合中的点直接连在集合头上,那么下次寻找就可以大大缩短寻找时间
路径合并:
一种基本的加速,有了路径合并的才叫并查集
本题中加速后的的复杂度大致是O(klogn),这个不给出证明了,比较复杂

若此时将把7的集合合并进5的集合里
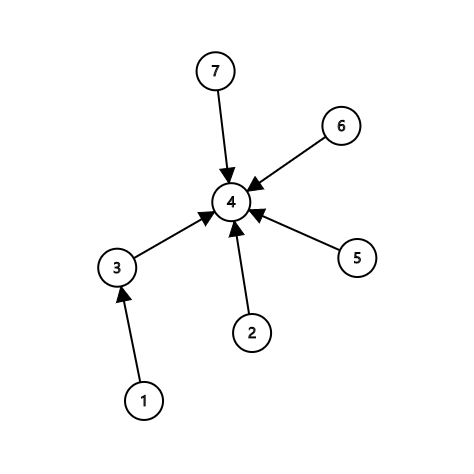
#include<bits/stdc++.h> #define maxn 1000010 using namespace std; int n,m,k,fa[maxn]; int find(int x){ int k=x; while(k!=fa[k]) k=fa[k]; while(x!=fa[x]){ int tmp=x; x=fa[x]; fa[tmp]=k; } return k; } int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); fa[find(u)]=find(v); } for(int i=1;i<=k;++i){ int u,v; scanf("%d%d",&u,&v); u=find(u); v=find(v); if(u==v) printf("Yes\n"); else printf("No\n"); } return 0; }
可以发现有明显的加速
常见版本:
更为常见的版本通常是递归进行的,因为这样方便(码量少),而且经常用合并函数进行
集合合并也包括集合附带属性的合并,用函数会显得比较简洁
#include<bits/stdc++.h> #define maxn 100010 using namespace std; int n,m,k,fa[maxn]; int find(int x){ if(x!=fa[x]) fa[x]=find(fa[x]); return fa[x]; } void merge(int x,int y){ int fa1=find(x),fa2=find(y); if(fa1==fa2) return; else fa[fa1]=fa2; } int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); merge(u,v); } for(int i=1;i<=k;++i){ int u,v; scanf("%d%d",&u,&v); int fa1=find(u),fa2=find(v); if(fa1==fa2) printf("Yes\n"); else printf("No\n"); } return 0; }
关于并查集按顺序连边:
并查集只能合并集合不能取消,如果要求减边,那么先用并查集合并到最后的结果再反过来加边即可。
如果按一定顺序连边就按照那个规则连就行了。
例题【洛谷P1111 修复公路】(按时间顺序连边)
#include<bits/stdc++.h> #define maxn 100010 using namespace std; int n,m,ans,fa[maxn]; struct node{ int x,y,t; }data[maxn]; bool cmp(node a,node b){ return a.t<b.t; } int find(int x){ if(x!=fa[x]) fa[x]=find(fa[x]); return fa[x]; } void merge(int x,int y){ int fa1=find(x),fa2=find(y); if(fa1==fa2) return; else{ fa[fa1]=fa2; ++ans; } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i) scanf("%d%d%d",&data[i].x,&data[i].y,&data[i].t); sort(data+1,data+m+1,cmp); for(int i=1;i<=m;++i){ merge(data[i].x,data[i].y); if(ans==n-1){ printf("%d",data[i].t); return 0; } } printf("-1"); return 0; }
关于连通块:
并查集可以做连通块的题目
目前连通块的个数=最开始的连通块数-并和次数
注意合并次数指两个不同的集合合并
例题【洛谷P1197 星球大战】(因为要减边所以反过来做+求连通块个数)
#include<bits/stdc++.h> #define maxn 400010 using namespace std; int n,m,k,ans,fa[maxn],pl[maxn]; bool v[maxn]; int head[maxn],edge_num; struct{ int to,nxt; }edge[maxn]; void add_edge(int from,int to){ edge[++edge_num].nxt=head[from]; edge[edge_num].to=to; head[from]=edge_num; } int find(int x){ if(x!=fa[x]) fa[x]=find(fa[x]); return fa[x]; } void merge(int x,int y){ int fa1=find(x),fa2=find(y); if(fa1==fa2) return; else fa[fa1]=fa2,--ans; } void Build(){ for(int i=1;i<=n;++i) fa[i]=i; ans=n; for(int i=1;i<=n;++i) if(!v[i]) for(int j=head[i];j;j=edge[j].nxt){ int to=edge[j].to; if(!v[to]) merge(i,to); } } void Solve(int x){ if(x==0) return; v[pl[x]]=false; for(int i=head[pl[x]];i;i=edge[i].nxt){ int to=edge[i].to; if(!v[to]) merge(pl[x],to); } int res=ans; Solve(x-1); printf("%d\n",res-x+1); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); add_edge(u+1,v+1); add_edge(v+1,u+1); } scanf("%d",&k); for(int i=1;i<=k;++i) scanf("%d",&pl[i]),pl[i]+=1,v[pl[i]]=true; Build(); int res=ans; Solve(k); printf("%d\n",res-k); return 0; }
关于带权并查集:
这些权值的处理可以根据并查集路径压缩的特质来处理
若是集合的权值,可以直接新建数组仿照fa[ ]的合并进而合并即可
另外有一点特别神奇,点的权值处理可以在路径压缩时进行处理
例题【洛谷P1196 银河英雄传说】
每在两列合并时,都需要将该列所有的战舰更新位置吗?
这样的话不就和最开始暴力“并查集”一样了吗。
我们可以发现,每列的战舰x的位置可以通过已知fa[x]更新出来
loc[x]表示以fa[x]为舰首时,x战舰的位置
只要进行一下两种操作即可
1.每次合并,先把i列舰首的位置更新出来,先处理i列舰首的位置,i列舰首的位置=j列的长度+1
2.我们规定只在路径压缩的时候更新该战舰的位置,那么第i列第x个战舰的真实位置即loc[x]=loc[fa[x]]+loc[x]-1
这里有点绕,理一理,当集合更新的后,loc[x]还是以fa[x]为舰首时的位置,而因为递归的缘故loc[fa[x]]已经更新完毕,
所以loc[fa[x]]是正确的,loc[x]目前看来是错误的
而更新完loc[x]后,再更新fa[x]值,fa[x]变为j列的舰头,此时loc[fa[x]]=1
为了使用fa[x]来处理loc所以并查集部分有变化
注意这题中合并要按顺序,是i列放在j列后面
#include<bits/stdc++.h> #define maxn 30010 using namespace std; int T,x,y; char ch; int fa[maxn],siz[maxn],loc[maxn]; int find(int x){ if(fa[x]==x) return x; int fath=find(fa[x]); loc[x]=loc[fa[x]]+loc[x]-1; fa[x]=fath; return fa[x]; } int main(){ scanf("%d",&T); for(int i=1;i<=maxn;++i) fa[i]=i,siz[i]=1,loc[i]=1; for(int i=1;i<=T;++i){ cin>>ch>>x>>y; int fa1=find(x),fa2=find(y); if(ch=='M') fa[fa1]=fa2,loc[fa1]=siz[fa2]+1,siz[fa2]+=siz[fa1]; else{ if(fa1!=fa2) printf("-1\n"); else printf("%d\n",abs(loc[y]-loc[x])-1); } } return 0; }
关于反集:
就是题目给定的规则,要好几个并查集一起操作
例题1【洛谷P1892 团伙】
关系整理(由于题目要求所以只需要连出友好线即可):
若p---敌--->q
p的敌人---友--->q的敌人
p的敌人---友--->q的朋友
q的敌人---友--->p的朋友
q的敌人---友--->p的敌人
若p---友--->q
p的朋友---友--->q的朋友
q的朋友---友--->p的朋友
把x+n的点当作x的敌人,那么n+1~n*2都是敌人集合
#include<bits/stdc++.h> using namespace std;
int father[10010]; int n,m,p,q,ans; char ch;
int find(int x) { if(father[x]!=x) father[x]=find(father[x]); return father[x]; }
int main(){ cin>>n>>m; for(int i=1;i<=2*n;i++) father[i]=i; for(int i=1;i<=m;i++){ cin>>ch>>p>>q; if(ch=='F') father[find(p)]=find(q); else{ father[find(n+p)]=find(q); father[find(n+q)]=find(p); } } for(int i=1;i<=n;i++) if(father[i]==i) ans++; cout<<ans; return 0; }
例题2【洛谷P2024 食物链】
类似于例1,这次是3个集合互连。
#include<bits/stdc++.h> #define maxn 100010 using namespace std; int n,m,fa[maxn*3],ans=0; int find(int x){ if(fa[x]!=x) fa[x]=find(fa[x]); return fa[x]; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=3*n;++i) fa[i]=i; for(int i=1;i<=m;++i){ int opt,x,y; scanf("%d%d%d",&opt,&x,&y); if(x>n||y>n){++ans;continue;} int fa1=find(x),fa2=find(y),fa3=find(x+n),fa4=find(y+n),fa5=find(x+n+n),fa6=find(y+n+n); //12同类 34猎物 56天敌 if(opt==1){ if(fa1==fa4||fa1==fa6) ++ans; else fa[fa1]=fa[fa2],fa[fa3]=fa[fa4],fa[fa5]=fa[fa6]; } else{ if(x==y){++ans;continue;} if(fa1==fa2||fa4==fa1) ++ans; else fa[fa6]=fa[fa1],fa[fa3]=fa[fa2],fa[fa5]=fa[fa4]; } } printf("%d",ans); }
关于特殊的区间覆盖的问题
如果一个题是区间覆盖,并且只查询最后的状态,那么这题的正解是并查集
因为是覆盖,最后的操作是会覆盖前面操作的,所以一般考虑反过来做
先执行最后的操作,然后再是前面的操作,将覆盖过的区间合并
例题【洛谷P2391 白雪皑皑】
题目中,把 (i*p+q)%N+1 和(i*q+p)%N+1 的染色 当作[L,R]区间的染色
先是反过来操作,先染最后一种颜色,再往前染,保证每一片雪花只染一次色
如果[L,R]区间的染色是从L染向R的大暴力,那么肯定会超时
当对一片雪花的操作结束时,这片雪花将不会再染,所以把这片雪花丢入一个集合,
这个集合用来加速从L走到R的过程,保证其每次都能给雪花染色,即跳过一连串的染过色雪花
集合的合并条件是相邻且染过色,这个集合维护一个值r,代表这个到了这个集合下一步应该走到r去染色
那么每次染[L,R]区间,从L开始走向R,每走的一个单位是一个集合的长度即跳到r位置,那么就可以跳过所有的染过色的部分
那么总的染色次数是n,复杂度是O(n+nlogn+2*m),而线段树的复杂度是O(n+m+nlogn+mlogn)
这题有很多细节,上面只是给个思路
#include<bits/stdc++.h> #define maxn 1000010 using namespace std; int n,m,p,q; int fa[maxn],col[maxn],lf[maxn],rt[maxn]; int find(int x){ if(fa[x]!=x) fa[x]=find(fa[x]); rt[fa[x]]=max(rt[fa[x]],rt[x]); //带权的合并 return fa[x]; } int main(){ scanf("%d%d%d%d",&n,&m,&p,&q); for(int i=1;i<=n;++i) rt[i]=i,fa[i]=i; for(int i=m;i>=1;--i){ int u=(1LL*i*p+q)%(1LL*n)+1,v=(1LL*i*q+p)%(1LL*n)+1; int l=min(u,v),r=max(u,v); while(l<r){ if(!col[l]) col[l]=i; //上色 int fath=find(l+1); //由于将当前和下一步合并,最右的染色范围是r,所以将r单独拎出来染 fa[find(l)]=fath; //合并染过色的雪花 l=rt[fath]; //更新下一步走的位置 } if(!col[r]) col[r]=i;//单独上色 } for(int i=1;i<=n;++i) printf("%d\n",col[i]); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号