正则化（L1和L2正则）

稀疏性表示数据中心0占比比较大

引西瓜书中P252原文：

 

 对于损失函数后面加入惩罚函数可以降低过拟合的风险，惩罚函数使用L2范数，则称为岭回归，L2范数相当与给w加入先验，需要要求w满足某一分布，L2范数表示数据服从高斯分布，而L1范数表示数据服从拉普拉斯分布。从拉普拉斯函数和高斯函数的图像上看，拉普拉斯函数取到0的概率更大，这样采用L1范数会有一些取到0

而且在小的数据是，L1比L2的惩罚力度大

 

我们对于最后的目标优化为 min D(w) + λ * R(w），其中R(w)表示正则项，然后我们转化为求解 min D(w), s.t. R(w) <= η。

 

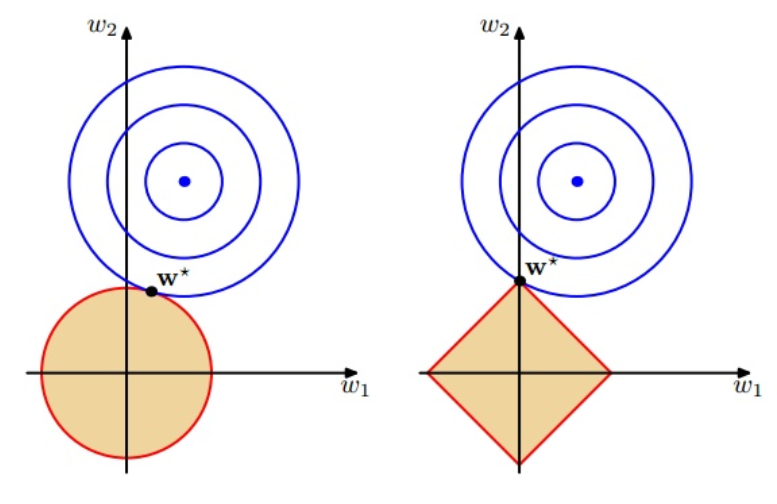
黄色区域为我们加入的惩罚项，转化以后相当于一个在黄色范围内求解最小值的一个过程。若相交为一篇区域，那么我们总能找到一点，在区域内，并且使得D(w)的值最小，最终图像会相切，其中λ越小限制范围越大，因为限制约小表明可以取的范围约大，所以橙色面积越大。

 

从数学公式的角度来说 L1 = |w1| + |w2| + ... + |wn| 导数 wi为1， 而L2 = 1/2 * (w1^2 + w2^2 + ... + wn^2）导数wi 为wi，取学习速率为λ， L1范数为：wi = wi - λ * 1，L2范数为 wi = wi - λ * wi，这样L1每次减去一个定值，总能减到0，而L2每次取自己的（1-λ），下降比较缓慢

参考链接：

https://www.zhihu.com/question/37096933 王小明，ser jamie

https://vimsky.com/article/969.html

《机器学习》 周志华