决策树 ID3,C4.5 CART
关于决策树
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据
缺点:可能会产生过度匹配问题
适用数据类型:数值型和标称型
ID3
ID3的决策树中主要使用了香农熵的概念,熵表示了数据的混乱程度,熵的值越大表示混乱程度越大
熵的计算公式为 H = -∑p(xi)log(P(xi)),表示P(xi)表示xi这种情况出现的概率
每次进行选择一个特征作为树的一层,选择层的原则是这样的。
先求出当前集合的熵值,然后爆枚每一种集合特征,然后对每一种特征在进行求小的熵值,然后作为这一类的熵值,每次选择最大的max(原本数据集的熵值 - 当前数据集的熵值)作为这一层的划分依据。
C4.5
C4.5是按照信息增益比率(gainratio)来进行划分的,增益比率通过引入一个被称作分裂信息(Splitinformation)的项来惩罚取值较多的Feature,分裂信息用来衡量Feature分裂数据的广度和均匀性:
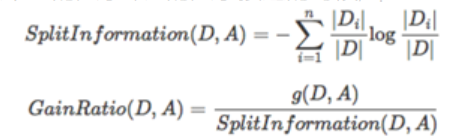
其中g(D,A)为熵函数
C4.5优缺点:
优点:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。
缺点:
(1)算法的计算效率较低,特别是针对含有连续属性值的训练样本时表现的尤为突出。
(2)算法在选择分裂属性时没有考虑到条件属性间的相关性,只计算数据集中每一个条件属性与决策属性之间的期望信息,有可能影响到属性选择的正确性。
CART
假设有K个类,样本点属于第k类的概率为![]() ,则概率分布的基尼指数定义为:
,则概率分布的基尼指数定义为:
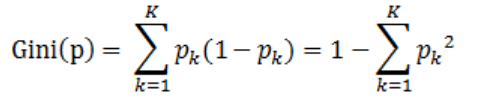
则在特征A的条件下,集合D的基尼指数定义为:
![]()
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大,样本集合的不确定性也就越大,这一点跟熵相似。
参考链接:
[1]https://blog.csdn.net/Andy_shenzl/article/details/83899431
[2]机器学习实战


