Codeforces Round #218 (Div. 2) 题解
- K-Periodic Array
题意:有n个数,有一个k,问最少修改几个数,使的a[i%k+1]都相等
思路:对每个位置都统计一下每种数字的出现次数,取最大值
代码:

#include <bits/stdc++.h> using namespace std; int n,k; int a[105]; int main() { scanf("%d%d", &n, &k); for(int i = 1; i <= n; i++) { scanf("%d",&a[i]); } int ans=0; for(int i = 1; i <= k; i++) { int cnt = 0,maxe = 0; map<int,int> mp; for(int j = i; j <= n; j += k) { mp[a[j]]++;cnt++; if(mp[a[j]]>maxe)maxe=mp[a[j]]; } ans+=cnt-maxe; } cout<<ans<<endl; return 0; }
B. Fox Dividing Cheese
题意:给出ab两个数字,每次可以对其中的一个数字*1/2,或者*1/3,或者*1/5,问最少几次可以使ab相等
思路:对ab进行2 3 5分解,看最后分解剩下的是否相等,如果不相等就打印-1,相等减去找到最小值
代码:

#include <bits/stdc++.h> using namespace std; int main() { int a,b; scanf("%d%d",&a,&b); int a2=0,a3=0,a5=0,b2=0,b3=0,b5=0; while(a%2==0)a/=2,a2++; while(a%3==0)a/=3,a3++; while(a%5==0)a/=5,a5++; while(b%2==0)b/=2,b2++; while(b%3==0)b/=3,b3++; while(b%5==0)b/=5,b5++; if(a!=b){ printf("-1\n"); } else{ printf("%d\n",abs(a2-b2)+abs(a3-b3)+abs(a5-b5)); } return 0; }
C. Hamburgers
题意:汉堡有BSC三种材料构成,先输入汉堡的配方,然后给出每种原料现在有多少,以及每种原料超市中的单价,以及你现在有多少钱,问最多可以做多少个汉堡
思路:对答案进行二分,然后判断做这么多汉堡需要多少钱
代码:

#include <bits/stdc++.h> using namespace std; typedef long long LL; char str[105]; LL cntb,cnts,cntc; LL numb,nums,numc; LL valb,vals,valc; LL a; bool check(LL x) { LL res = 0; LL as = x * cntb - numb; if(as > 0) res += as * valb; as = x * cnts - nums; if(as > 0) res += as * vals; as = x * cntc - numc; if(as > 0) res += as * valc; if(res <= a)return true; return false; } int main() { scanf("%s",str+1); cin>>numb>>nums>>numc; cin>>valb>>vals>>valc; cin>>a; int len = strlen(str+1); cntb = 0; cntb = 0; cntc = 0; for(int i = 1; i <= len; i++) { if(str[i] == 'B')cntb++; if(str[i] == 'S')cnts++; if(str[i] == 'C')cntc++; } LL l = 0,r = 1e15; LL ans = 0; while(l <= r){ LL mid =(l + r) >> 1; if(check(mid)){ l = mid + 1; ans = mid; } else r = mid - 1; } cout<< ans <<endl; return 0; }
D. Vessels
题意:有一个n(2e5)层的容器,每一层的容量为ai,每一层满了以后就会自动流入到下一层,有两种操作,一种是向第i层加入xi的水,第二种操作是查询第x层现在有多少水,
思路:用一个类似于跳表的东西维护每一层如果满了下一层流向哪里
代码:

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=2e5+7; int a[maxn],now[maxn]; int fa[maxn]; int n; int update(int id,int val) { if(now[id] + val <= a[id]) { now[id] += val; return id; } val = now[id] + val - a[id]; now[id] = a[id]; fa[id] = update(fa[id],val); return fa[id]; } int main() { scanf("%d",&n); for(int i = 1; i <= n; i++) { scanf("%d",&a[i]); fa[i] = i+1; } a[n+1]=1e15; int q; scanf("%d",&q); while(q--){ int op; scanf("%d",&op); if(op==1) { int as, qw; scanf("%d%d",&as,&qw); update(as, qw); } else { int as; scanf("%d",&as); printf("%d\n",now[as]); } } return 0; }
E. Subway Innovation
题意:在数轴上有n(3e5)个点,从中选出k个点,使的这k个点的价值最小,k个点的价值为这k个点中任意两个点的距离之和
思路:对数轴上的点排序,因为让最后答案最小,所以最后的点集肯定是数轴上连续的k个点,假设选了[l,r]的k个点,与[l+1,r+1]的关系是
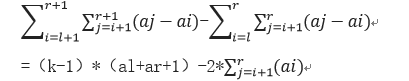
所以排序以后,直接On维护求出最小值即可
代码:

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=3e5+7; struct node { int id; LL val; bool operator <(const node &b)const { return val < b.val; } }; node a[maxn]; LL pre[maxn]; int main() { int n; scanf("%d",&n); for(int i = 1; i <= n; i++) { LL x; scanf("%lld",&x); node as; as.id = i; as.val = x; a[i] = as; } int K; scanf("%d",&K); sort(a + 1, a + 1 + n); for(int i = 1; i <= n; i++) { pre[i] = pre[i - 1] + a[i].val; } LL res = 0; for(int i = 1; i <= K; i++) { res += (i - 1) * a[i].val - pre[i - 1]; } LL maxe = res; int k=1; for(int i = K + 1; i <= n; i++) { res += (K - 1) * (a[i].val + a[i - K].val) - 2 * (pre[i - 1] - pre[i - K]); if(res < maxe) { maxe = res; k = i - K + 1; } } for(int i = k; i < K + k; i++) { printf("%d ",a[i].id); } puts(""); return 0; }



