我理解的数据结构(三)—— 队列(Queue)
我理解的数据结构(三)—— 队列(Queue)
一、队列
- 队列是一种线性结构
- 相比数组,队列对应的操作是数组的子集
- 只能从一端(队尾)添加元素,只能从另一端(队首)取出元素
- 队列是一种先进先出的数据结构(FIFO)
二、数组队列与循环队列
1. 数组队列
如果你有看过我之前的文章不要小看了数组或者栈,你就会发现,自己封装一个数组队列是如此的轻松加愉快!
(1)先定义一个接口,接口中定义队列需要实现的方法
``` public interface Queue<E> { int getSize(); boolean isEmpty(); // 查看队首元素 E getFront(); // 入队 void enqueue(E ele); // 出队 E dequeue(); } ```(2)实现数组队列
``` public class ArrayQueue<E> implements Queue<E> {// 这里的数组是在之前的文章中封装好的,直接拿来用就好了
private ArrayNew<E> array;
public ArrayQueue(int capacity) {
array = new ArrayNew<>(capacity);
}
public ArrayQueue() {
this(10);
}
public int getCapacity() {
return array.getCapacity();
}
@Override
public int getSize() {
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
@Override
public E getFront() {
return array.getFirst();
}
@Override
public void enqueue(E ele) {
array.addLast(ele);
}
@Override
public E dequeue() {
return array.removeFirst();
}
@Override
public String toString() {
StringBuffer res = new StringBuffer();
res.append(String.format("arrayQueue: size = %d, capacity = %d\n", getSize(), getCapacity()));
res.append("front [");
for (int i = 0; i < array.getSize(); i++) {
res.append(array.get(i));
if (i != getSize() - 1) {
res.append(", ");
}
}
res.append("] tail");
return res.toString();
}
}
<p><strong>(3)数组队列的复杂度</strong></p>
<table>
<thead><tr>
<th align="center">方法</th>
<th align="center">复杂度</th>
</tr></thead>
<tbody>
<tr>
<td align="center"><code>enqueue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>dequeue</code></td>
<td align="center">O(n)</td>
</tr>
<tr>
<td align="center"><code>front</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>getSize</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>isEmpty</code></td>
<td align="center">O(1)</td>
</tr>
</tbody>
</table>
<blockquote>这个时候我们会发现,在进行出队操作的时候,数组队列的复杂度是0(n),如果我们频繁的进行出队操作,那么其实数组队列的效率是很低的,如何提升数组队列的性能呢?这个时候我们就要用到循环队列了。</blockquote>
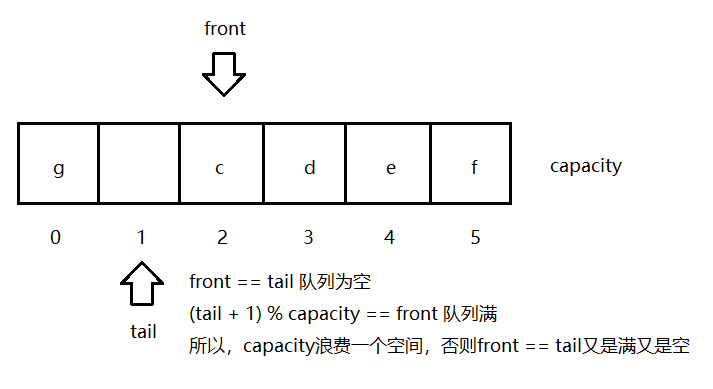
<h4>2. 循环队列队列</h4>
<blockquote>循环队列的原理:</blockquote>
<ol>
<li>
<code>dequeue</code>时,不要在去除队首元素时,把整体向前移动</li>
<li>维护 <code>front</code> 、 <code>tail</code> 和 <code>size</code> 这三个属性</li>
<li>
<code>enqueue</code>的时候<code>tail++</code>
</li>
<li>
<code>dequeue</code>的时候<code>front++</code>
</li>
</ol>
<p><strong>(1)实现循环队列</strong></p>
public class LoopQueue<E> implements Queue<E> {
private E[] array;
private int size;
private int front;
private int tail;
public LoopQueue(int capacity) {
// 我们需要浪费一个空间去判断队列是否已满,所以需要把capacity + 1
array = (E[])new Object[capacity + 1];
front = 0;
tail = 0;
size = 0;
}
public LoopQueue() {
this(10);
}
// 返回用户传递的队列大小
public int getCapacity() {
return array.length - 1;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return front == tail;
}
@Override
public E getFront() {
if (isEmpty()) {
throw new IllegalArgumentException("Queue is empty. Can't get front.");
}
return array[0];
}
@Override
public void enqueue(E ele) {
if (front == (tail + 1) % array.length) {
// 扩展队列长度为原长度2倍
resize(getCapacity() * 2);
}
array[tail] = ele;
size++;
tail = (tail + 1) % array.length;
}
@Override
public E dequeue() {
if (isEmpty()) { // 队列为空
throw new IllegalArgumentException("Queue is empty. Can't get dequeue.");
}
E ele = array[front];
size--;
array[front] = null;
front = (front + 1) % array.length;
if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
resize(getCapacity() / 2);
}
return ele;
}
private void resize(int newCapacity) {
E[] newArray = (E[]) new Object[newCapacity + 1];
for (int i = 0; i < size; i++) {
newArray[i] = array[(front + i) % array.length];
}
array = newArray;
front = 0;
tail = size;
}
@Override
public String toString() {
StringBuffer res = new StringBuffer();
res.append(String.format("queue: size = %d, capacity = %d\n", getSize(), getCapacity()));
res.append("front [");
// 循环条件,和循环增量都要注意下
for (int i = front; i != tail; i = (i + 1) % array.length) {
res.append(array[i]);
if ((i + 1) % array.length != tail) {
res.append(", ");
}
}
res.append("] tail");
return res.toString();
}
}
<p><strong>(2)循环队列的复杂度</strong></p>
<table>
<thead><tr>
<th align="center">方法</th>
<th align="center">复杂度</th>
</tr></thead>
<tbody>
<tr>
<td align="center"><code>enqueue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>dequeue</code></td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center"><code>front</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>getSize</code></td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center"><code>isEmpty</code></td>
<td align="center">O(1)</td>
</tr>
</tbody>
</table>
<h3>三、用时间说话</h3>
<p><strong>(1)用时方法</strong></p>
public static double test(Queue<Integer> q, int opCount) {
// 纳秒
long startTime = System.nanoTime();
Random random = new Random();
for (int i = 0; i < opCount; i++) {
q.enqueue(random.nextInt(Integer.MAX_VALUE));
}
for (int i = 0; i < opCount; i++) {
q.dequeue();
}
// 纳秒
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
<p><strong>(2)调用</strong></p>
// 十万次入队和十万次出队操作
int opCount = 100000;
ArrayQueue<Integer> aq = new ArrayQueue<>();
double time1 = test(aq, opCount);
System.out.println(time1);
LoopQueue<Integer> lq = new LoopQueue<>();
double time2 = test(lq, opCount);
System.out.println(time2);
<p><strong>(3)结果</strong></p>
<ul>
<li>14.635995113</li>
<li>0.054536447</li>
</ul>
<blockquote>这个就是算法和数据结构的力量!</blockquote>
原文地址:https://segmentfault.com/a/1190000016147024


