6 计算机的运算方法

6.1 无符号数和有符号数 

6.3 定点运算

6.2 数的定点表示和浮点表示 

6.4 浮点四则运算

6.5 算术逻辑单元 

 

 

 

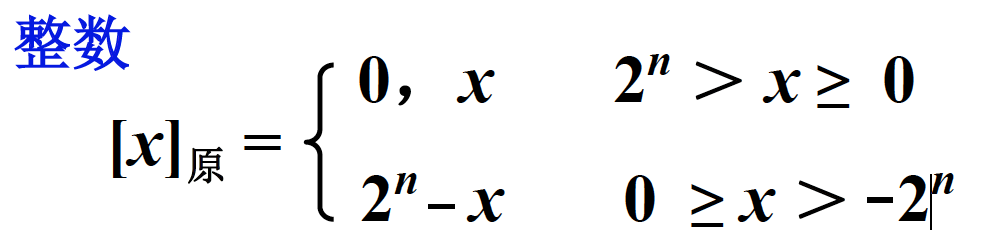
 解析一下：这是从数学上描述的负数的原码的表示：

x的原码的真值 = 2^n的真值 - x的真值，也就是2^n的真值 减去 x的真值得到的数的二进制表示就是x的原码。

比如-2, 2^2 - -2 = 6 ，所以-2的原码表示 是6的原码110

x是负数时，|x|+2^n = -x +2^n = 2^n - x

例如 -2 即 2^2 - (-2) ，也就是100 - -10 = 110，就是2的原码

 

减一个数 = 加上该数的补数。

即A-B= A+B的补数 = A + （模-B）

钟表中（mod 12），时针回调4h，则 6 -4 =2 =  6 + 8

 

 

 

 

 

 

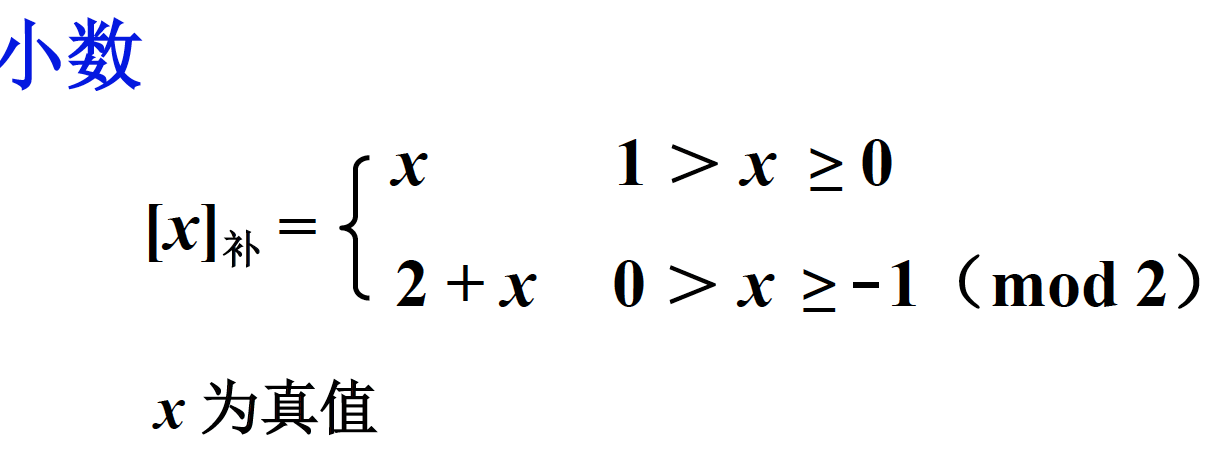
负数的模因为需要加符号位的原因，比通常意义的模大一倍。

 

 

 证明：

因为：

x原 = 2^n - x真

x补 = 2^(n+1) + x真

所以：

x原= 2^(n+1) - (x补-2^n) = （n+1）个1  - (x补-2^n)  +1 

所以x原 是

x补符号位保持不变，每位取反，末位加1 。

 

 

 对于正数，原码 = 补码 = 反码 

 对于负数 ，符号位为 1，其 数值部分 

原码除符号位外每位取反末位加 1  -> 补码

原码除符号位外每位取反 -> 反码 

 

 

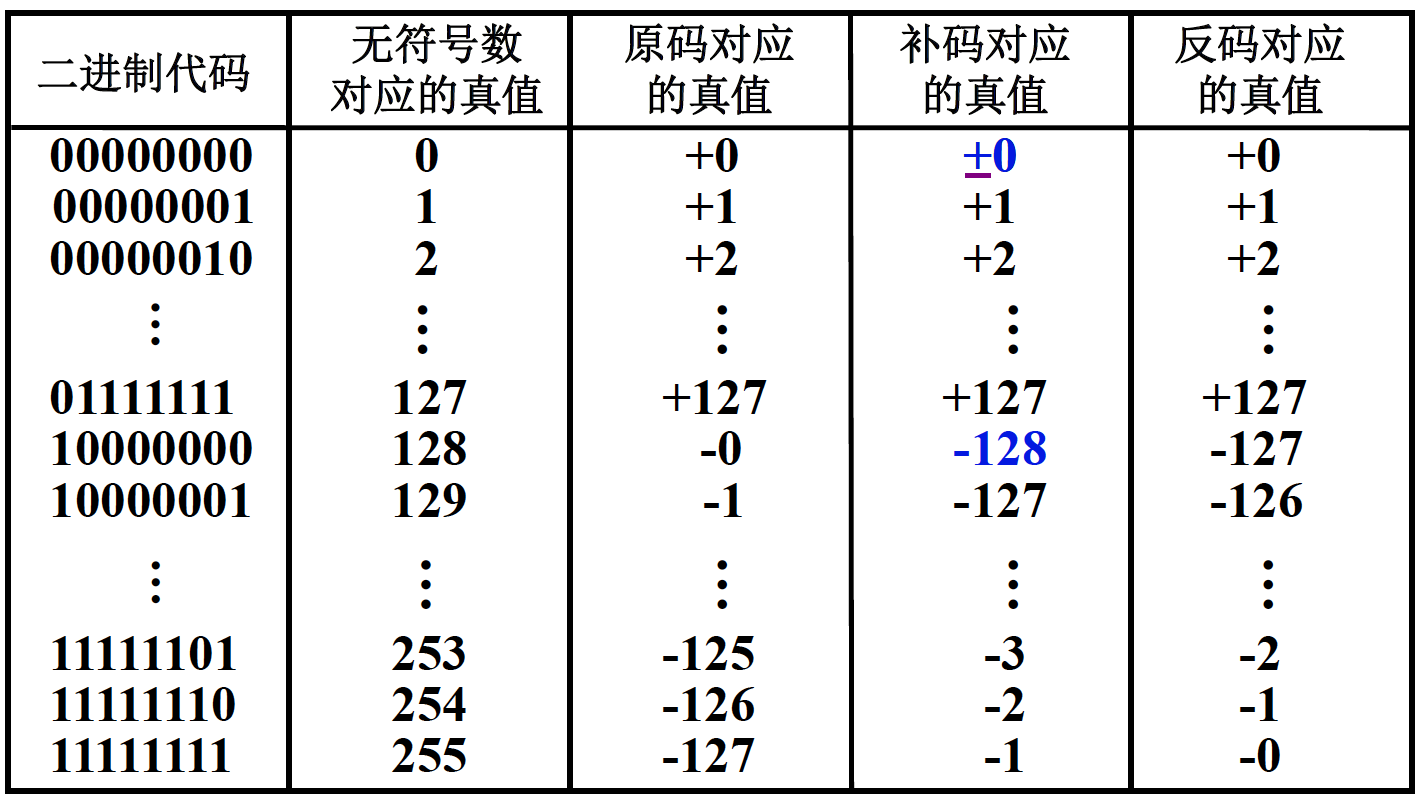
 根据上图可以看出，1和-127的补码的整数部分是一样的，

所以求-127的补码时，可以转换为求-1的原码

互为正负数的补码相加为2^(n+1)

对于<=0的数，

给出补码求真值：模减去整数位，添加正负号。

给出反码求真值: 模减去整数位+1，添加正负号。

 

移码是把补码符号位取反

 

 

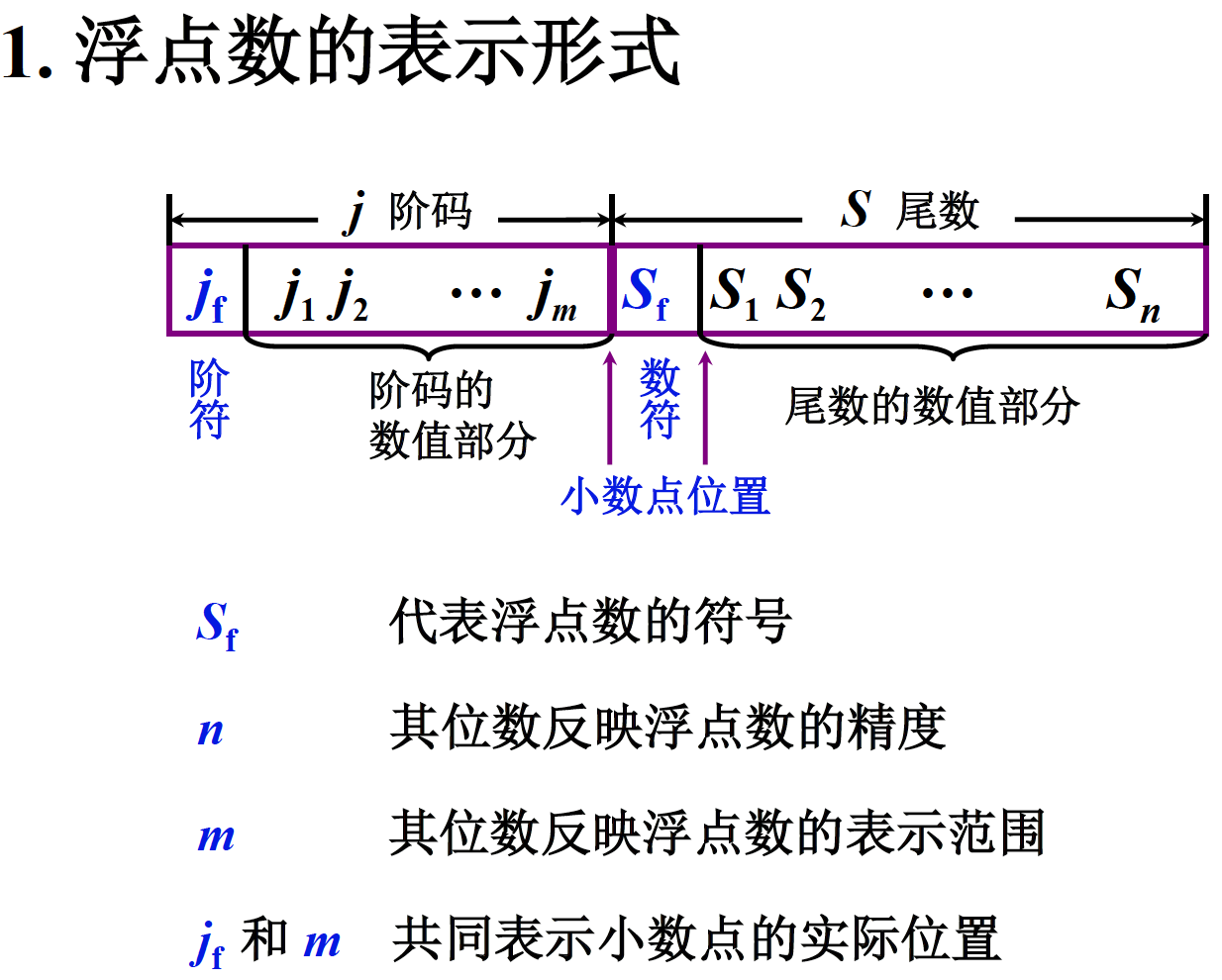
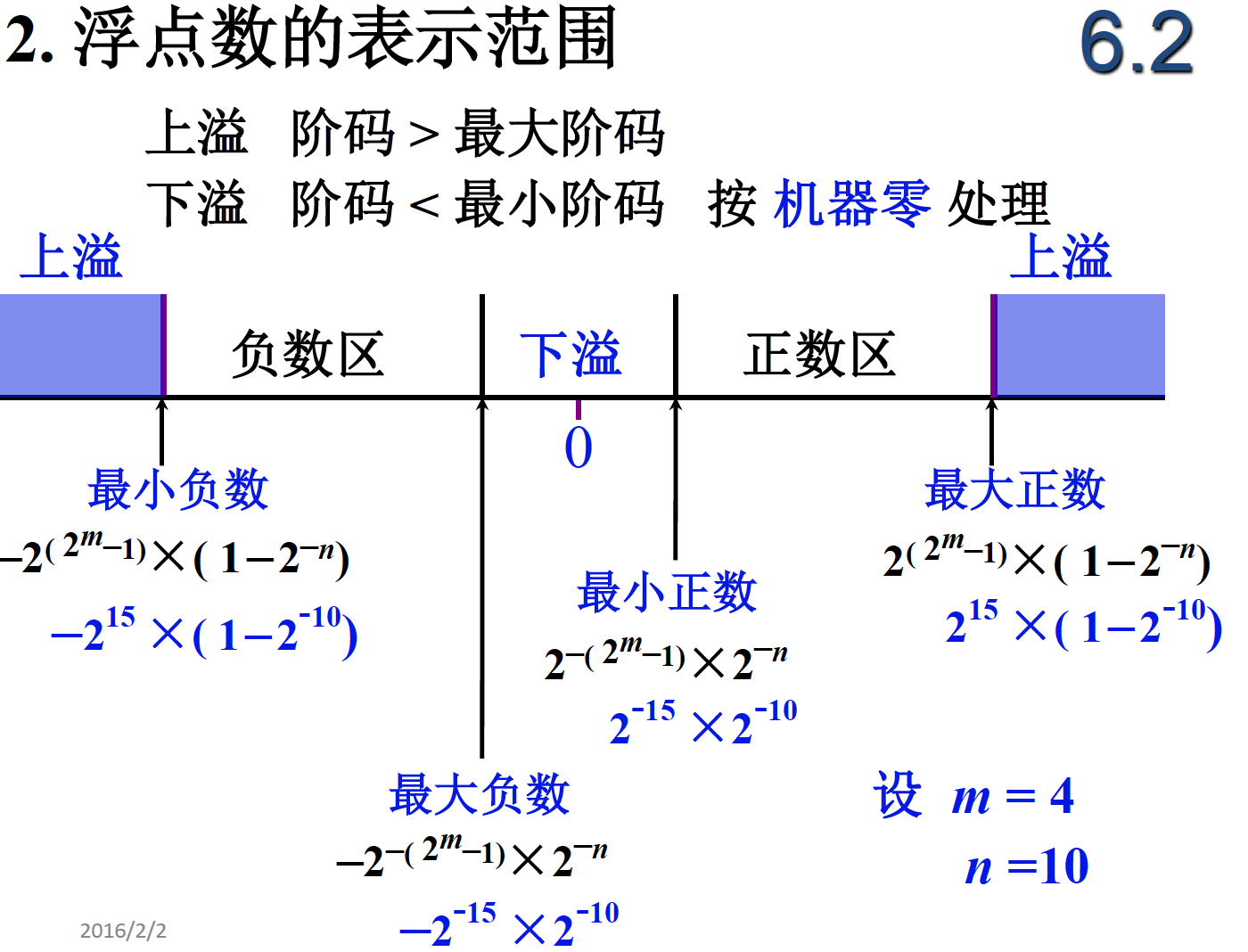
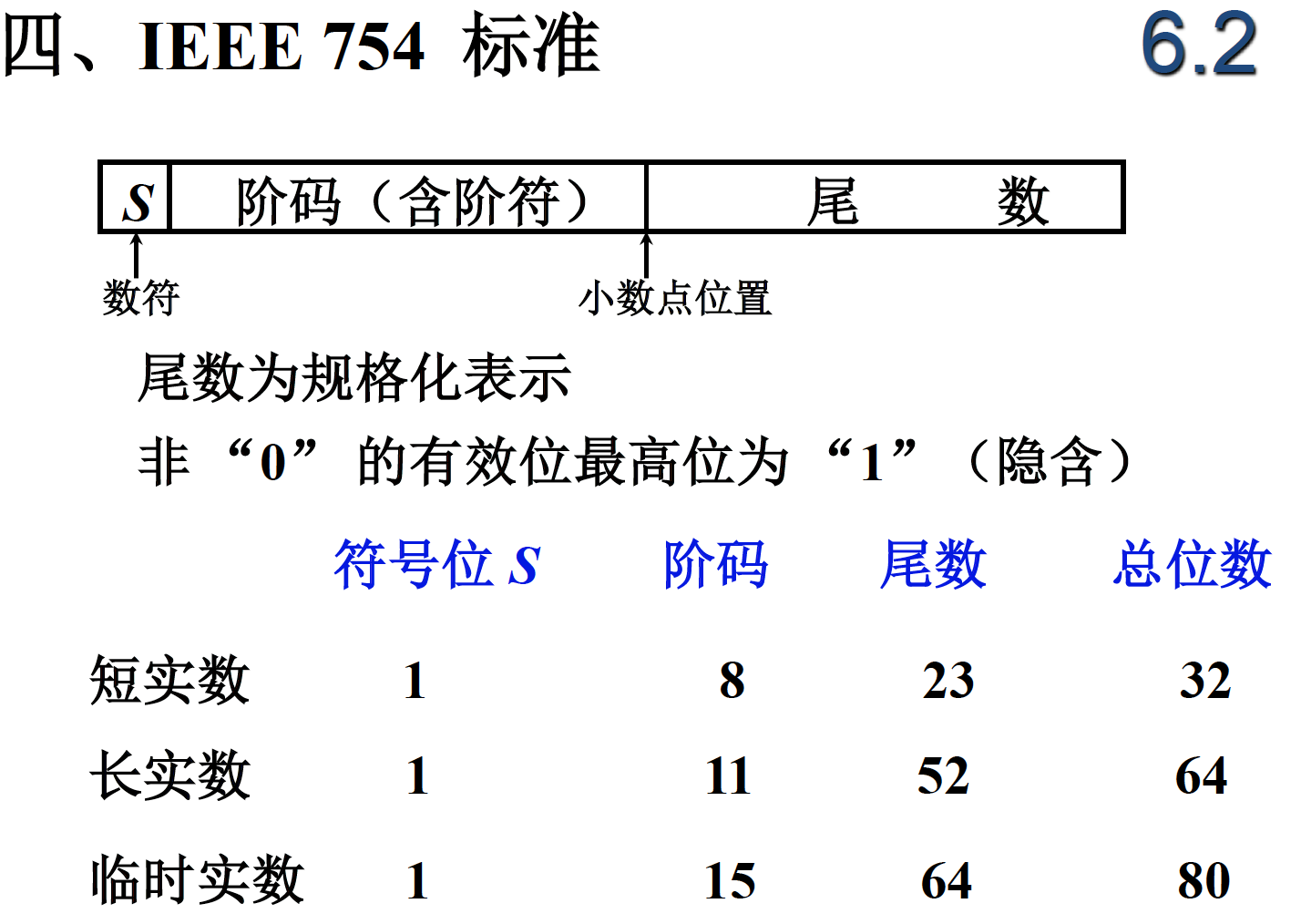
规格化浮点数的原因：为了更大的精确度。

规格化浮点数，要求小数点后一位不能是0，必须是1。
   （有点像科学计数法，但是和科学计数法比起来，小数点要左移一位。  ）

比如位数是2位情况下，

计算 0.1*0.1 = 0.01*2^1  *   0.01*2^1 = 0.0001*2^2,因为尾数只有2位，所以得到0.00*2^2，丢失精度。

如果规格化，0.1*0.1 = 0.1*2^0  *   0.1*2^0= 0.01*2^0,因为尾数只有2位，所以得到0.01*2^0，最大可能保留精度

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

注意，补码右移时，比如：-13>>2 = 7

 

算术移位和逻辑移位的区别 

算术移位  有符号数的移位 

逻辑移位  无符号数的移位 

 

 

 

 

 

 

 

 

 

 

 

 

 

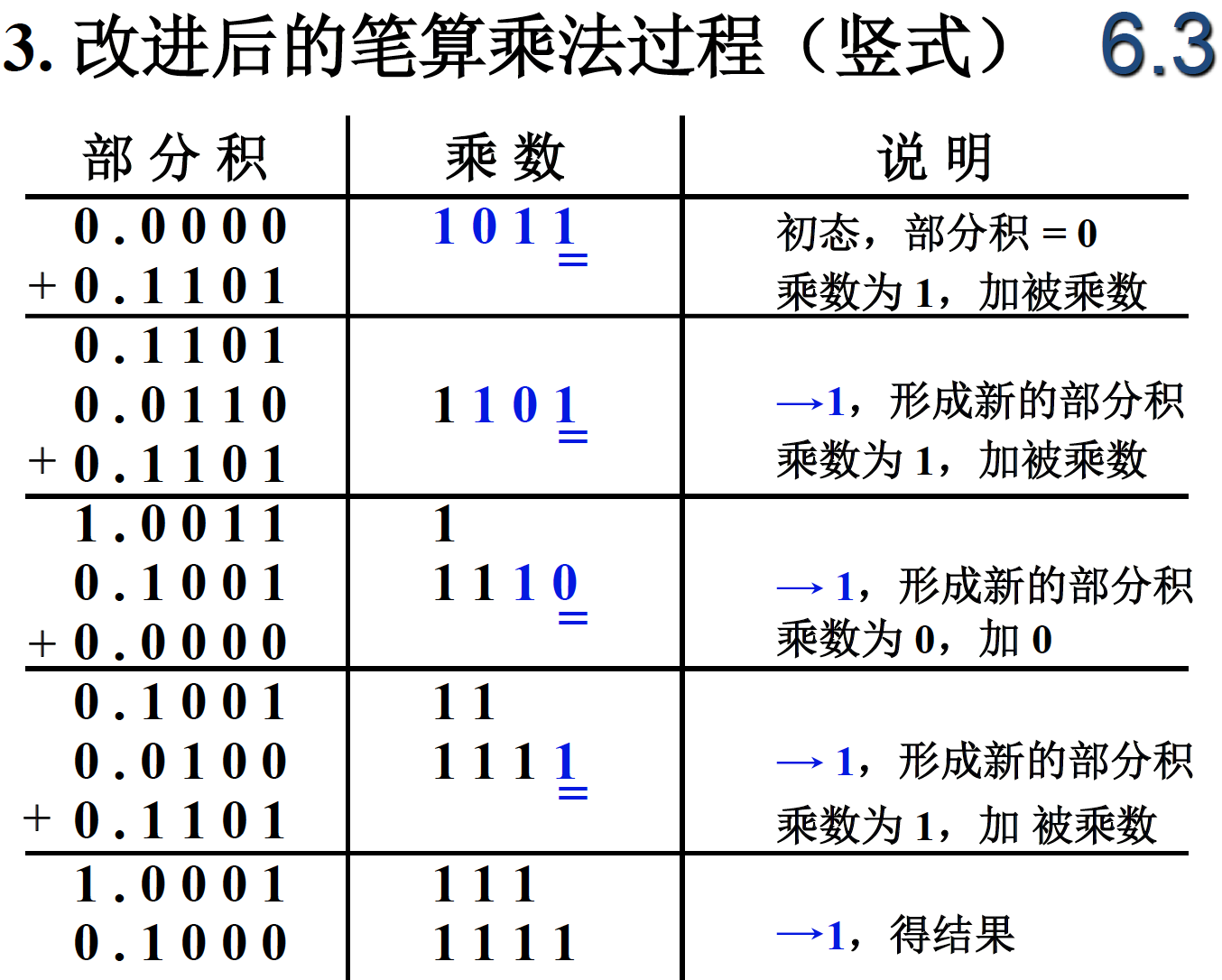
 一个寄存器保存被乘数，一个保存乘数，一个保存符号位

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

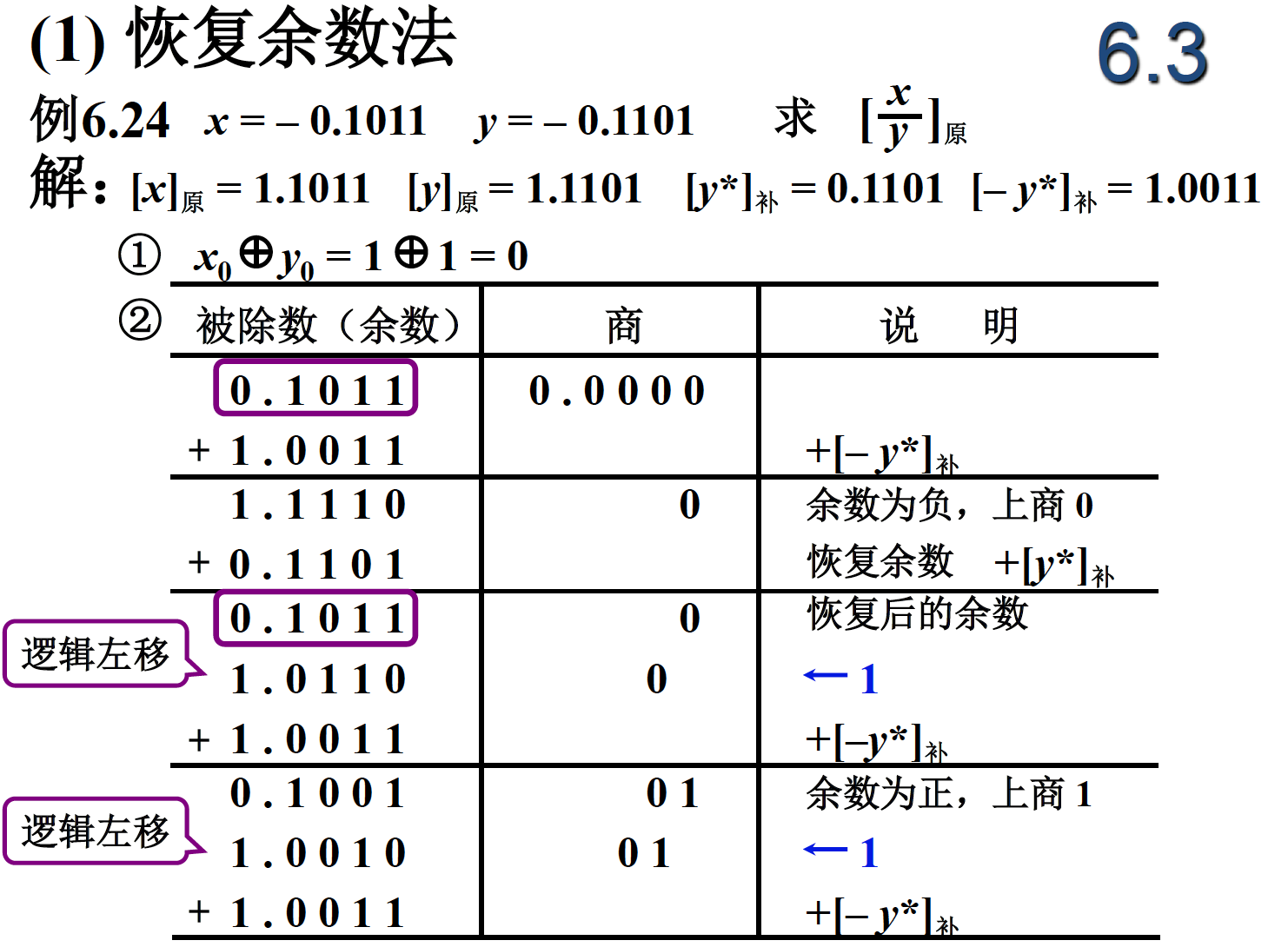
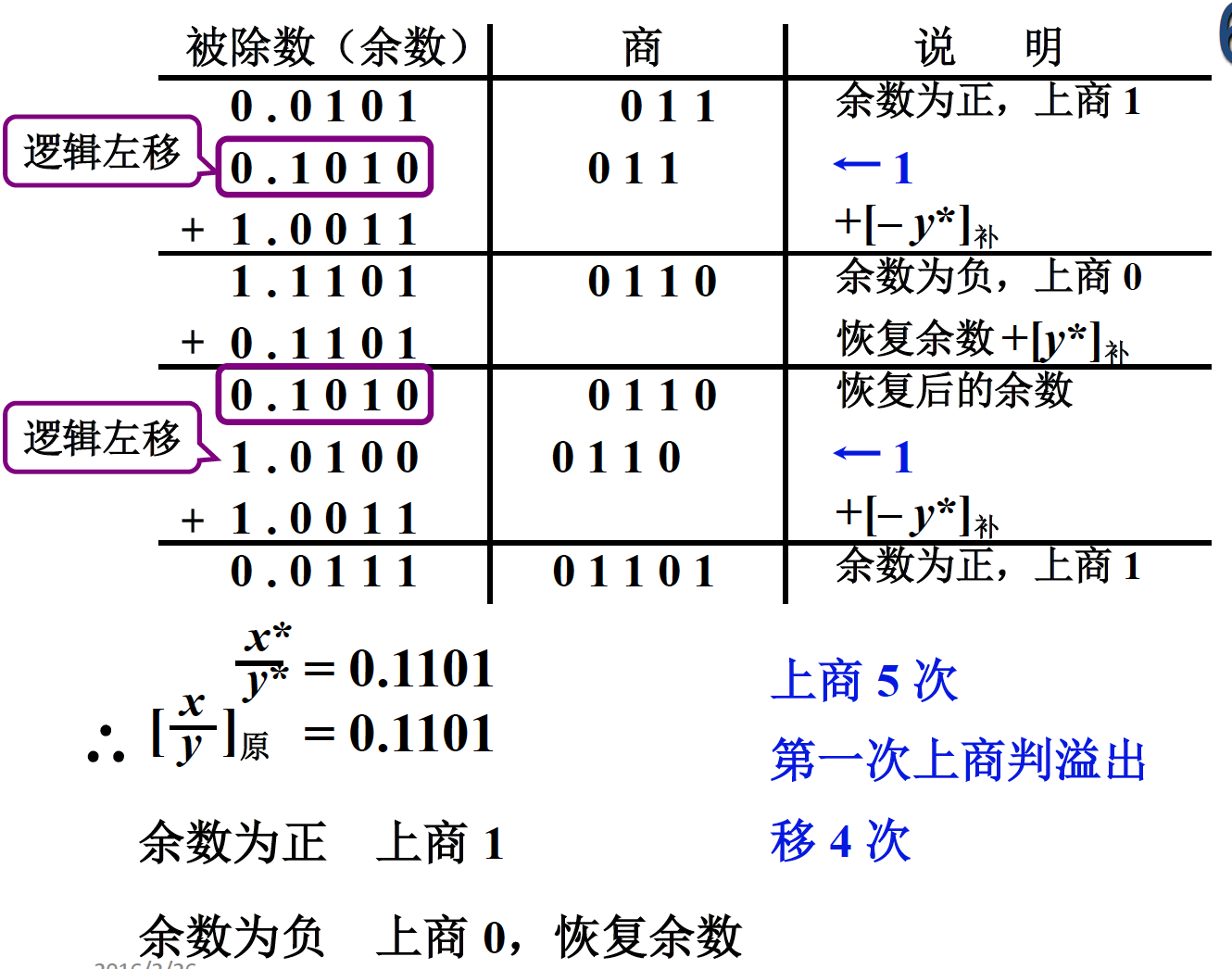
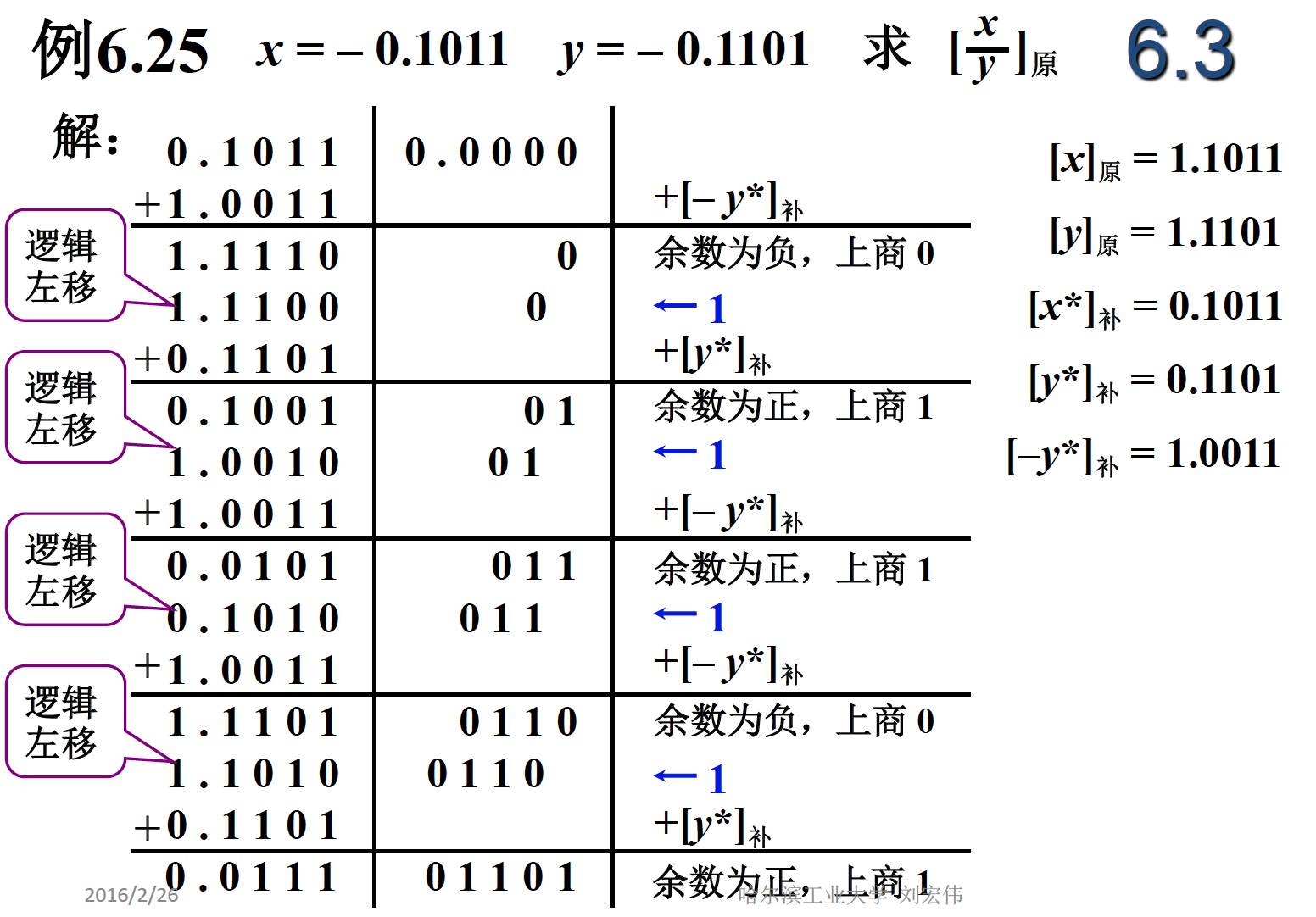
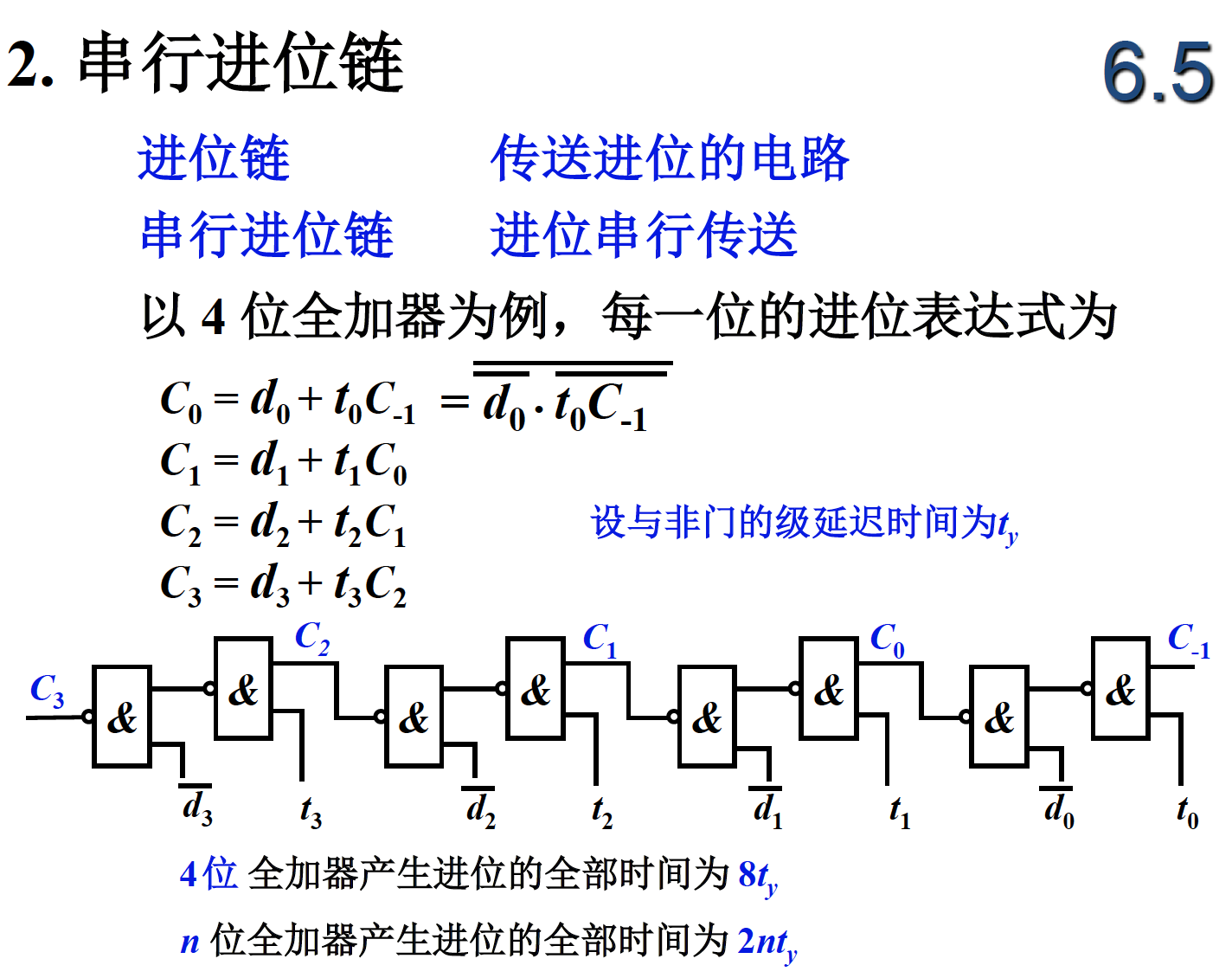
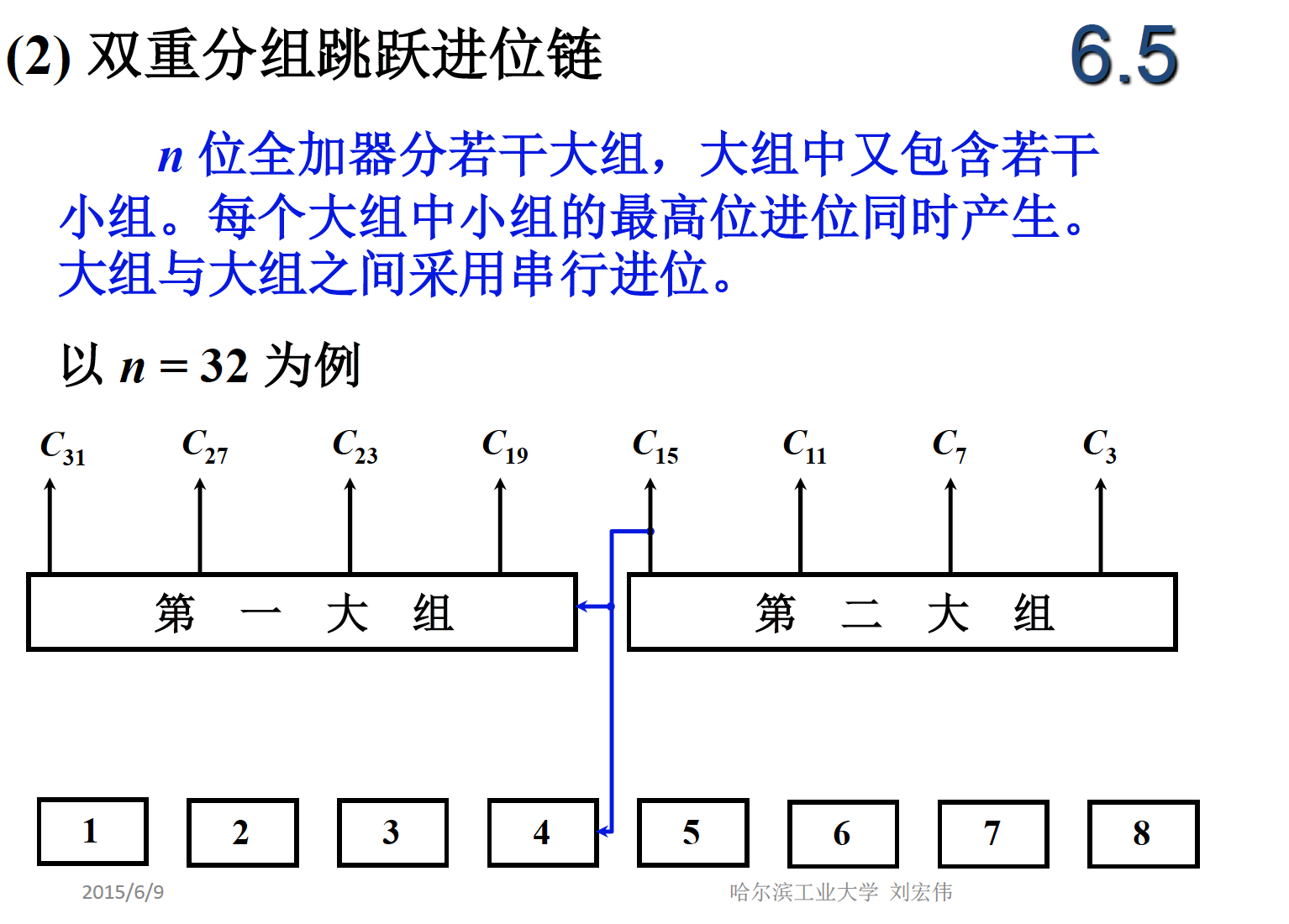
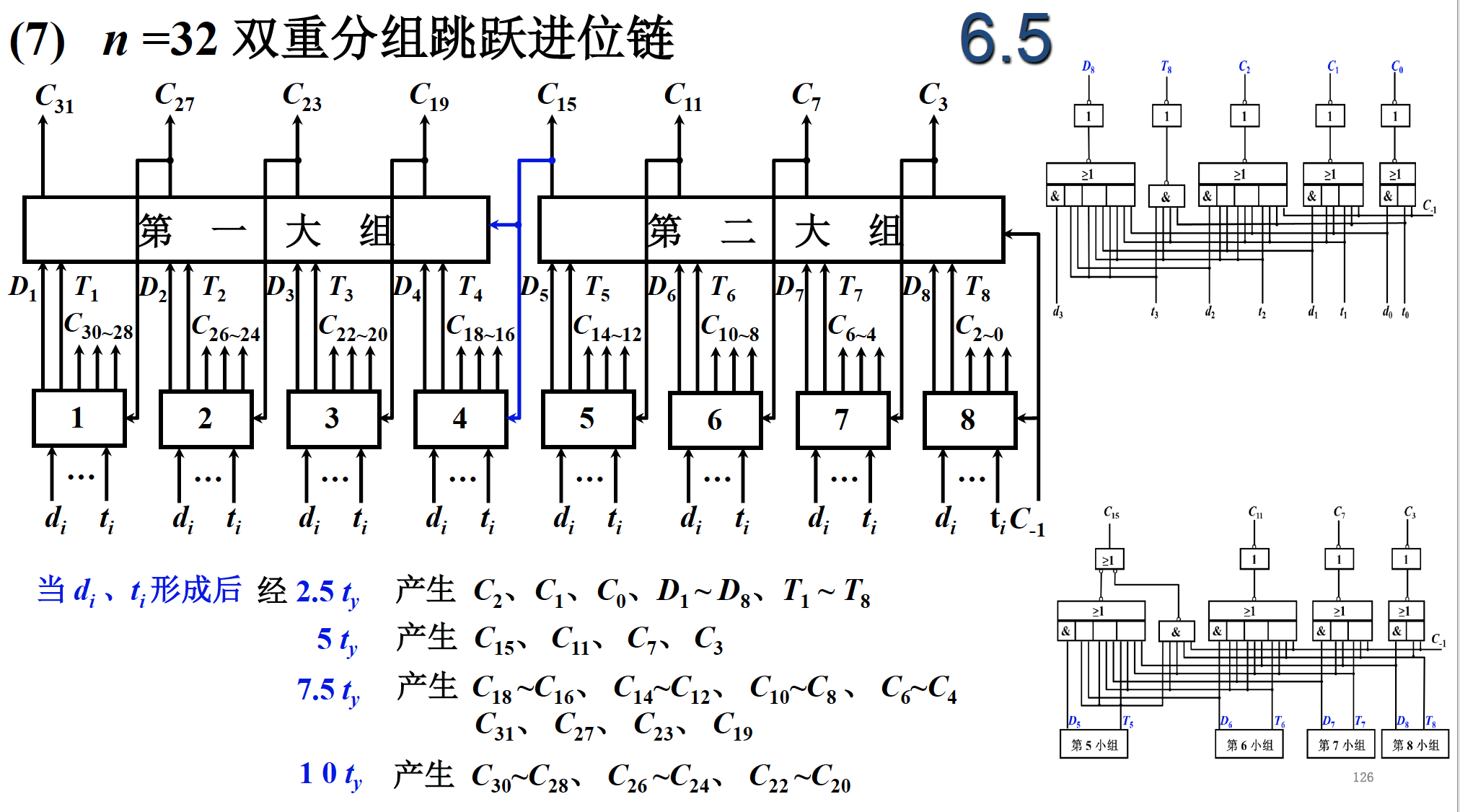
串行为时间为 2n

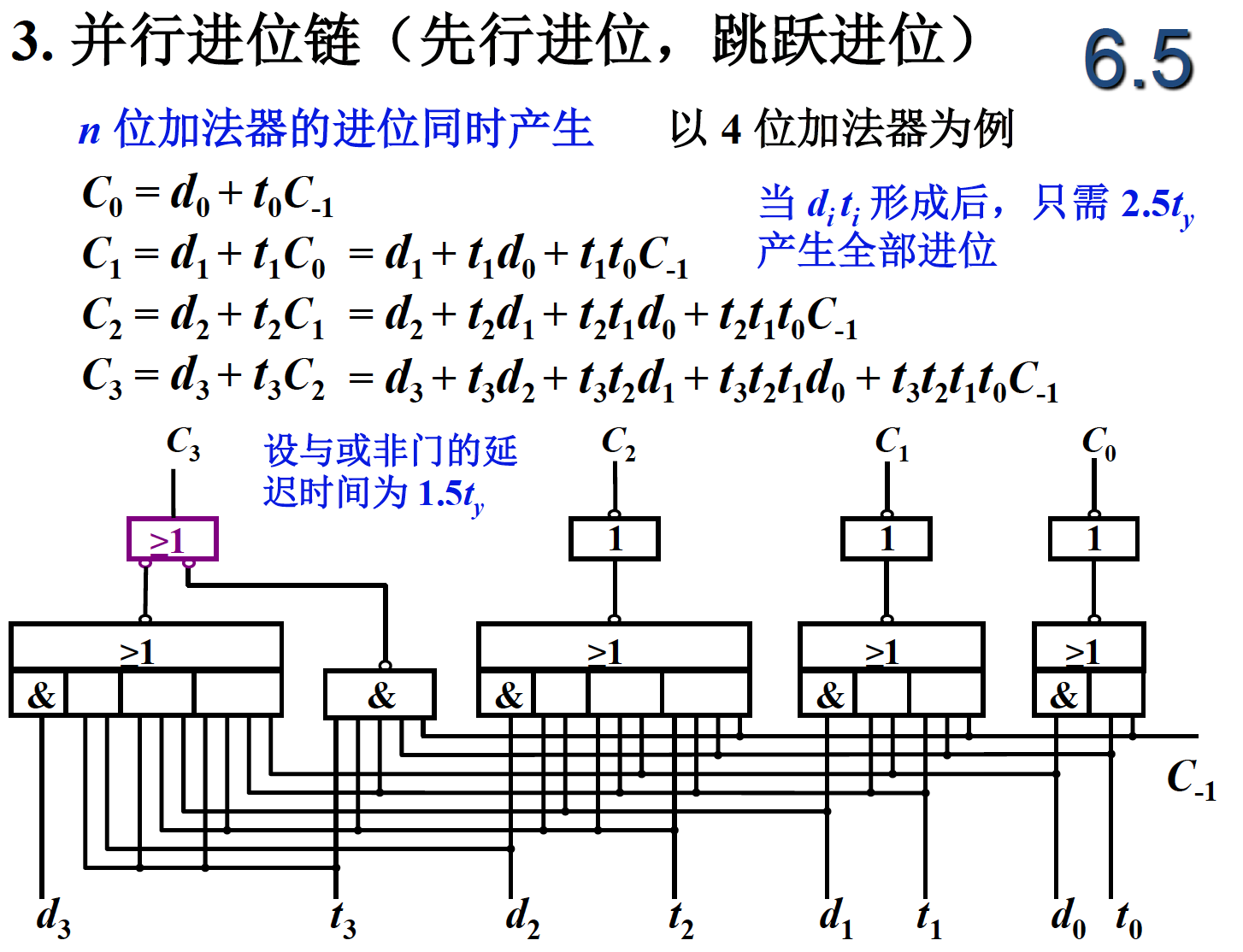
并行为 2.5

单重分组为 2.5*组数

多重分组为 2.5*（重数+1）

一般为串并混合，下图的时间为 2.5*3 +2.5 = 10