[ZJOI2007]最大半连通子图

【题目描述】：
最大半连通子图

【思路】：
首先题目本身要求子图是半联通的，也就是意味着我们所要求的子图不一定是一个强联通分量，但是我们仔细分析题目之后，很容易得出以下结论：

• 虽然要求的是半联通子图，但是我们从任意一个强联通分量\(E\)，连到另外一个强联通分量\(F\)，则集合\(V(E,F)\)一定是一个半联通子图。假设我们已经找到了答案的点集\(V={E_1,E_2....E_n}\)，那么最大半联通子图的值就是\(\sum_{E_i\in V}sum[E_i]\)

于是就可以考虑\(tarjan\)缩点，将整个图缩为\(DAG\)，接下来就要考虑这样一个问题：

• 如何在一个\(DAG\)上找这个半联通子图？

先来思考这样一个问题，由于\(DAG\)是无环的，所求的半联通子图，要求满足\(\forall u,v \;\in \;E\)，都有\(u ->v || v->u\)成立，比如这样一个图：

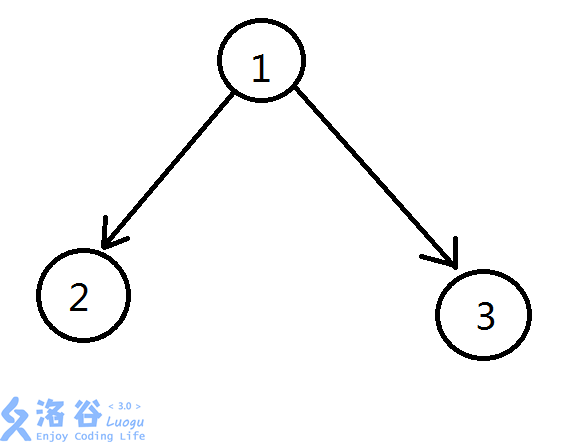
它不是半联通的，因为点\(2,3\)并不满足条件。
那么我们通过\(dp\)来决策出这个半联通子图。先进行一次拓扑排序，预处理出每个节点的\(dis[]\)数组，表示以这个节点为终点时最大的\(size\)值。在依次删除入读为\(0\)的点时，我们可以像最短路计数一样，决策出\(way\)数组，表示以这个点为终点的路径有多少条，方程应该很容易得到

• \(if(dis[v] == dis[u] + size[v]) \;way[v] += way[u]\)

最后把答案累加起来就行了，但这个题千万别忘了——

去重边！！

因为在缩点的时候，可能会引进重边，而重边会对路径条数有影响。。

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;

int n,m,mod;

const int MAXN = 100005;
const int MAXM = 1000005;

struct edge{
    int u,v,nxt;
}e[MAXM];int head[MAXN];int cnt = 0;int dfn[MAXN];int low[MAXN];int s[MAXN];bool vis[MAXN];int tot = 0;int id = 0;int Bcnt = 0;
int size[MAXN];int x[MAXM];int y[MAXM];int in[MAXN];int dis[MAXN];int way[MAXN];int maxx = -inf;int b[MAXN];

inline void add(int u,int v){
    e[++cnt].u = u;e[cnt].v = v;e[cnt].nxt = head[u];head[u] = cnt;
}

inline void tarjan(int x){
    dfn[x] = low[x] = ++id;
    s[++tot] = x;vis[x] = 1;

    for(int i=head[x];i;i=e[i].nxt){
        int v = e[i].v;
        if(!dfn[v]){
            tarjan(v);
            low[x] = min(low[x] , low[v]);
        }
        else if(vis[v]) low[x] = min(low[x] , dfn[v]);
    }

    if(low[x] == dfn[x]){
        int j = -1;Bcnt++;
        while(j ^ x){
            j = s[tot--];
            b[j] = Bcnt;
            vis[j] = 0;
            size[Bcnt]++;
        }
    }
}

queue<int>q;
inline void topo(){
    for(int i=1;i<=Bcnt;++i){
        if(!in[i]){
            q.push(i);
            dis[i] = size[i];
            way[i] = 1;
            maxx = max(maxx , dis[i]);
        }
    }
    
    while(!q.empty()){
        int u = q.front() ;q.pop() ;
        for(int i=head[u];i;i=e[i].nxt){
            int v = e[i].v;
            in[v]--;
            if(!in[v]) q.push(v);
            if(dis[v] < dis[u] + size[v]){
                dis[v] = dis[u] + size[v];
                way[v] = 0;
                maxx = max(maxx , dis[v]);
            }
            if(dis[v] == dis[u] + size[v]){
                way[v] += way[u];
                way[v] %= mod;
            }
        }
    }
}

inline bool cmp(int a,int b){
    if(x[a] ^ x[b]) return x[a] < x[b];
    return y[a] < y[b];
}

int order[MAXM];
inline void remove(){
    for(int i=1;i<=m;++i){
        order[i] = i;
        x[i] = b[x[i]];
        y[i] = b[y[i]];
    }
    sort(order+1,order+1+m,cmp);
}

int main(){
    scanf("%d%d%d",&n,&m,&mod);
    for(int i=1;i<=m;++i){
        int u,v;scanf("%d%d",&u,&v);
        x[i] = u;y[i] = v;
        add(u,v);
    }

    for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
    
    remove();
    memset(head,0,sizeof head);cnt = 0;
    for(int i=1;i<=m;++i){
    	int z = order[i];
    	if((x[z] ^ y[z]) && (x[z] ^ x[order[i-1]] || y[z] ^ y[order[i-1]])){
    		in[y[z]]++;
    		add(x[z] , y[z]);
        }
    }
    
    topo();
    int ans = 0;
    for(int i=1;i<=Bcnt;++i){
    	if(dis[i] == maxx) ans += way[i],ans %= mod;
    }
    printf("%d\n%d",maxx , ans);
    return 0;
}