注:原创不易,转载请务必注明原作者和出处,感谢支持!
一 写在开头
1.1 本文内容
前段时间在复习随机过程的时候发现高中的三角函数相关知识已经忘得差不多了。本来在高中的时候,三角函数这一块就没怎么学得很好。因此,趁着现在有空,倒回去再重新系统地学习一遍三角函数的相关知识。
本文内容为三角函数的相关知识。先理清基本概念再对涉及到的公式进行证明。
二 基本概念
2.1 角度概念的推广
- 正角:按照逆时针旋转形成的角
- 负角:按照顺时针旋转形成的角
- 第几象限的角:使角的顶点与坐标原点重合,角的始边和x轴正半轴重合,这时,角的终边在第几象限就是第几象限角。注意,如果终边在坐标轴上,则认为该角不属于任何象限
- 弧度制:以弧度为单位(rad)为单位来度量角的制度叫做弧度制
弧度的来源:设在半径为\(r\)的圆周上有一个角度大小为\(\alpha = n^{\circ}\)的圆弧,其弧长为\(l\)。则该角度的弧度值定义为其所对应的弧长和半径的比值:
\[\frac{l}{r} = n \cdot \frac{2\pi}{360}
\]
从弧度的定义易知一个圆周\(360^{\circ}\)对应的弧度值为\(2\pi\)。
2.2 三角函数的引入
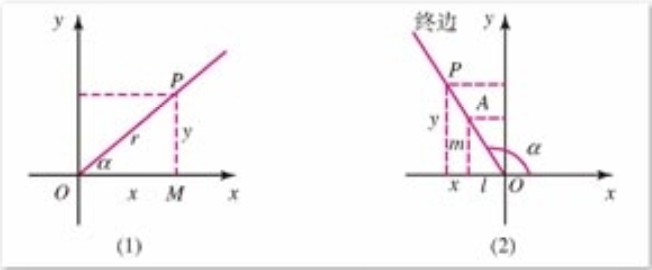
如上图所示,设一端点在坐标原点\(O\)处的射线上有一点\(P\),\(P\)在x轴和y轴上的投影分别为\(x\)和\(y\),且线段\(OP\)的长度为\(r\),其与x轴正半轴形成的夹角大小为 \(\alpha\),则所涉及的三角函数如下表所示。
| 函数 | 名称 |
|--------|--------|--------|
| \(sin~\alpha = \frac{y}{r}\) | 正弦 |
| \(cos~\alpha = \frac{x}{r}\) | 余弦 |
| \(tan~\alpha = \frac{y}{x}\) | 正切 |
| \(sec~\alpha = \frac{1}{cos~\alpha} = \frac{r}{x}\) | 正割 |
| \(csc~\alpha = \frac{1}{sin~\alpha} = \frac{r}{y}\) | 余割 |
| \(cot~\alpha = \frac{1}{tan~\alpha} = \frac{x}{y}\) | 余切 |
易知三角函数之间的基本关系式:
\[sin^2\alpha + cos^2\alpha = 1
\]
\[tan~\alpha = \frac{sin~\alpha}{cos~\alpha}
\]
并且,显然有(\(k\)为整数):
\[cos(\alpha + k \cdot 2\pi) = cos~\alpha
\]
\[sin(\alpha + k \cdot 2\pi) = sin~\alpha
\]
\[tan(\alpha + k \cdot 2\pi) = tan~\alpha
\]
接下来的一些内容实在是不想写了,因为太简单了。(其实是因为用LaTex写公式有点麻烦,太懒......)
三 三角恒等变换
3.1 合角公式
下面是一些三角恒等变换和它们的证明思路
\[cos(\alpha - \beta) = cos~\alpha cos~\beta + sin~\alpha sin~\beta
\]
上述式子的证明其实相当简单。令\(\alpha\)和\(\beta\)分别为两个单位向量的夹角,利用了两个向量的点积的两种不同计算方法,它们结果相等即可导出上述公式。具体的过程可以参见高中数学课本。有了上述公式可以导出下面三个合角公式。
\[\begin{equation}
\begin{split}
cos(\alpha + \beta) &= cos\left[\alpha - (-\beta)\right]\\
&= cos\alpha cos(-\beta) + sin\alpha sin(-\beta)\\
&= cos\alpha cos\beta - sin\alpha sin\beta
\end{split}
\end{equation}
\]
同样,还有:
\[\begin{equation}
\begin{split}
sin(\alpha + \beta) &= cos\left[\frac{\pi}{2} - (\alpha + \beta)\right]\\
&= cos\left[(-\alpha + \frac{\pi}{2}) - \beta\right]\\
&= cos(-\alpha + \frac{\pi}{2})cos~\beta + sin(-\alpha + \frac{\pi}{2})sin~\beta\\
&= sin~\alpha cos~\beta + cos~\alpha sin~\beta
\end{split}
\end{equation}
\]
以及:
\[\begin{equation}
\begin{split}
sin(\alpha - \beta) &= sin\left[\alpha + (-\beta)\right]\\
&= sin~\alpha cos(-\beta) + cos~\alpha sin(-\beta)\\
&= sin~\alpha cos~\beta - cos~\alpha sin~\beta
\end{split}
\end{equation}
\]
因此,四个合角公式可以总结如下:
\[cos(\alpha + \beta) = cos~\alpha cos~\beta - sin~\alpha sin~\beta
\]
\[cos(\alpha - \beta) = cos~\alpha cos~\beta + sin~\alpha sin~\beta
\]
\[sin(\alpha + \beta) = sin~\alpha cos~\beta + cos~\alpha sin~\beta
\]
\[sin(\alpha - \beta) = sin~\alpha cos~\beta - cos~\alpha sin~\beta
\]
3.2 两角和与差的正切
对于两个角的合角的正切,有:
\[\begin{equation}
\begin{split}
tan(\alpha + \beta) &= \frac{sin(\alpha + \beta)}{cos(\alpha + \beta)}\\
&= \frac{sin~\alpha cos~\beta + cos~\alpha sin~\beta}{cos~\alpha cos~\beta - sin~\alpha sin~\beta}\\
&= \frac{\frac{sin~\alpha cos~\beta + cos~\alpha sin~\beta}{cos~\alpha cos~\beta}}{\frac{cos~\alpha cos~\beta - sin~\alpha sin~\beta}{cos~\alpha cos~\beta}}~~~(cos~\alpha cos~\beta \neq 0)\\
&= \frac{tan~\alpha + tan~\beta}{1 - tan~\alpha tan~\beta}
\end{split}
\end{equation}
\]
从而有:
\[\begin{equation}
\begin{split}
tan(\alpha - \beta) &= tan\left[\alpha + (-\beta)\right]\\
&= \frac{tan~\alpha + tan(-\beta)}{1 - tan~\alpha tan(-\beta)}\\
&= \frac{tan~\alpha - tan~\beta}{1 + tan~\alpha tan~\beta}
\end{split}
\end{equation}
\]
故,两个角的合角的正切可总结如下:
\[tan(\alpha + \beta) = \frac{tan~\alpha + tan~\beta}{1 - tan~\alpha tan~\beta}
\]
\[tan(\alpha - \beta) = \frac{tan~\alpha - tan~\beta}{1 + tan~\alpha tan~\beta}
\]
3.3 倍角公式和半角公式
在上述的合角公式中,令\(\alpha = \beta\),即可得到如下的倍角公式:
\[sin~2\alpha = 2sin~\alpha cos~\alpha
\]
\[\begin{equation}
\begin{split}
cos~2\alpha &= cos^2\alpha - sin^2\alpha\\
&= 2cos^2\alpha - 1\\
&= 1 - 2sin^2\alpha
\end{split}
\end{equation}
\]
\[tan~2\alpha = \frac{2tan~\alpha}{1-tan^2 \alpha}
\]
由上述的倍角公式可以很容易地推出下列的半角公式:
\[cos~\frac{\alpha}{2} = \pm \sqrt{\frac{1 + cos~\alpha}{2}}
\]
\[sin~\frac{\alpha}{2} = \pm \sqrt{\frac{1 - cos~\alpha}{2}}
\]
\[tan~\frac{\alpha}{2} = \pm \sqrt{\frac{1-cos~\alpha}{1 + cos~\alpha}}
\]
正负号由角\(\frac{\alpha}{2}\)所在的象限决定。
3.4 积化和差与和差化积公式
下面通过上面的4个合角公式来推导积化和差与和差化积公式。
4个合角公式如下:
\[cos(\alpha + \beta) = cos~\alpha cos~\beta - sin~\alpha sin~\beta
\]
\[cos(\alpha - \beta) = cos~\alpha cos~\beta + sin~\alpha sin~\beta
\]
\[sin(\alpha + \beta) = sin~\alpha cos~\beta + cos~\alpha sin~\beta
\]
\[sin(\alpha - \beta) = sin~\alpha cos~\beta - cos~\alpha sin~\beta
\]
积化和差公式的推导如下:
\[\begin{equation}
\begin{split}
cos~\alpha cos~\beta &= \frac{1}{2}(2cos~\alpha cos~\beta)\\
&= \frac{1}{2}(cos~\alpha cos~\beta + sin~\alpha sin~\beta + cos~\alpha cos~\beta - sin~\alpha sin~\beta)\\
&= \frac{1}{2}\left[cos(\alpha + \beta) + cos(\alpha - \beta)\right]
\end{split}
\end{equation}
\]
\[\begin{equation}
\begin{split}
sin~\alpha sin~\beta &= \frac{1}{2}(2sin~\alpha sin~\beta)\\
&= \frac{1}{2}(cos~\alpha cos~\beta + sin~\alpha sin~\beta - cos~\alpha cos~\beta + sin~\alpha sin~\beta)\\
&= \frac{1}{2}\left[ cos(\alpha - \beta) - cos(\alpha + \beta)\right]\\
&= -\frac{1}{2}\left[ cos(\alpha + \beta) - cos(\alpha - \beta)\right]
\end{split}
\end{equation}
\]
\[\begin{equation}
\begin{split}
sin~\alpha cos~\beta &= \frac{1}{2}(2sin~\alpha cos~\beta)\\
&= \frac{1}{2}(sin~\alpha cos~\beta + cos~\alpha sin~\beta + sin~\alpha cos~\beta - cos~\alpha sin~\beta)\\
&= \frac{1}{2}\left[ sin(\alpha + \beta) + sin(\alpha - \beta)\right]
\end{split}
\end{equation}
\]
\[\begin{equation}
\begin{split}
cos~\alpha sin~\beta &= \frac{1}{2}(2cos~\alpha sin~\beta)\\
&= \frac{1}{2}(sin~\alpha cos~\beta + cos~\alpha sin~\beta + cos~\alpha sin~\beta - sin~\alpha cos~\beta)\\
&= \frac{1}{2}\left[ sin(\alpha + \beta) - sin(\alpha - \beta)\right]
\end{split}
\end{equation}
\]
由上述的积化和差公式可得:
\[cos(\alpha + \beta) + cos(\alpha - \beta) = 2cos~\alpha cos~\beta
\]
\[cos(\alpha + \beta) - cos(\alpha - \beta) = -2sin~\alpha sin~\beta
\]
\[sin(\alpha + \beta) + sin(\alpha - \beta) = 2sin~\alpha cos~\beta
\]
\[sin(\alpha + \beta) - sin(\alpha - \beta) = 2cos~\alpha sin~\beta
\]
令\(x = \alpha + \beta, y = \alpha - \beta\),则可得和差化积公式如下:
\[cos~x + cos~y = 2cos\frac{x+y}{2}cos\frac{x-y}{2}
\]
\[cos~x - cos~y = -2sin\frac{x+y}{2}sin\frac{x-y}{2}
\]
\[sin~x + sin~y = 2sin\frac{x+y}{2}cos\frac{x-y}{2}
\]
\[sin~x - sin~y = 2cos\frac{x+y}{2}sin\frac{x-y}{2}
\]
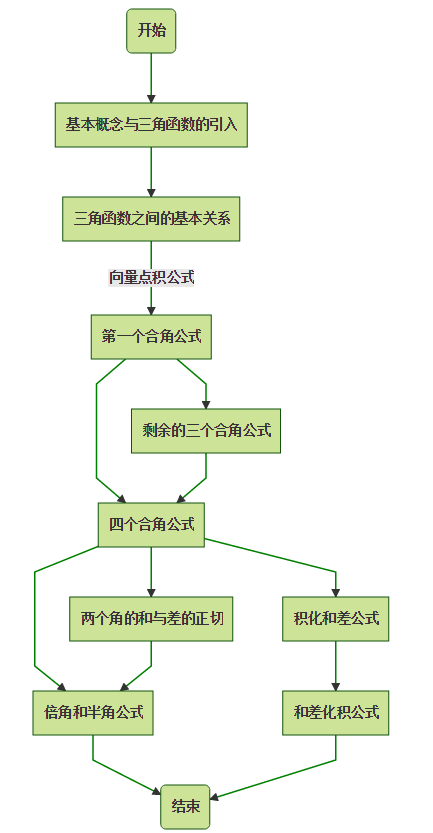
四 公式之间的依赖逻辑
五 参考资料




