浅析特征值与特征向量

最近在学习算法常常遇到特征值和特征向量的问题，一直都一知半解没有领悟到本质。因此特意查阅了相关资料，自己的理解写一篇小结。

1. 矩阵乘法的本质

首先，我们来看一个线性方程式。为了更简洁的表示，我们常常使用矩阵乘法。

\[\begin{cases} 2x+y=m \\ 3x+2y=n \end{cases} -> \left[ \begin{matrix} 2 & 1\\ 3 & 2\end{matrix} \right]\left[ \begin{matrix} x\\ y\end{matrix} \right]=\left[ \begin{matrix} m\\ n\end{matrix} \right] \]

线性方程式将x,y变化到m,n经过一个线性变换。同理，向量[x,y]与一个矩阵的乘积,得到向量[m,n]，其实就相当于将这个向量[x,y]进行了线性变换。变换矩阵为：

\[\left[ \begin{matrix} 2 & 1\\ 3 & 2\end{matrix} \right] \]

因此，一个矩阵其实就是一个线性变换。

2.矩阵乘法的几何意义

为了更加直观的理解矩阵乘法（线性变换）的几何意义，我们看另一个变换矩阵A：

\[A=\left[ \begin{matrix} 2 & 0\\ 0 & 0.5\end{matrix} \right] \]

考虑下面的图像，绿色正方形说明施加到三个向量上的线性变换A。
可以看出在这种情况下变换仅仅是水平方向乘以因子2和垂直方向乘以因子0.5。同时，具体的几何表现是向量进行了旋转或拉伸。

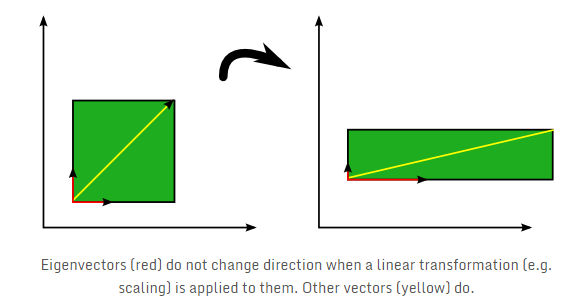
其中，我们可以看到三个向量中的红色向量在线性变换时其方向保持不变，仅在该方向上进行了伸缩。这些向量就是线性变换的特征向量(描述这个矩阵变化方向)，在特征向量的方向伸缩的值即为特征值(描述在这个方向上变化的大小)。
这些特征向量和特征值可以唯一地定义方形矩阵A。

3.特征向量和特征值的定义

教科书里面是这样定义的，A是n阶矩阵，如果数\(\lambda\)和n维非零列向量x使关系式：

\[Ax = \lambda x \]

成立，那么这样的数\(\lambda\)称为矩阵A的特征值，非零向量x称为A对应于特征值\(\lambda\)的特征向量。
上式也可写成

\[(A- \lambda E) x =0 \]

该齐次线性方程组有非零解的充分必要条件是系数行列式

\[|A- \lambda E| =0 \]

左边\(|A- \lambda E|\)为\(\lambda\)的特征多项式。该式为矩阵A的特征方程，特征方程的解即为A的特征值。n阶矩阵A在复数范围内有n个特征值。

例如，计算矩阵

\[\left[ \begin{matrix} 3 & -1\\ -1 & 3\end{matrix} \right] \]

的特征值和特征向量。
解： A的特征多项式为

\[|A- \lambda E| = \left| \begin{matrix} 3-\lambda & -1\\ -1 & 3-\lambda\end{matrix} \right| =(3-\lambda)^2 -1=(4-\lambda)(2-\lambda)=0 \]

所以A的特征值为：\(\lambda_1\)=2, \(\lambda_2\)=4

当\(\lambda_1\)=2时，对应的特征向量应满足

\[\left( \begin{matrix} 3-2 & -1\\ -1 & 3-2\end{matrix} \right)\left( \begin{matrix} x_1\\ x_2\end{matrix} \right)=\left( \begin{matrix} 0\\ 0\end{matrix} \right) \]

解得\(x_1=x_2\),所以特征向量可取为

\[p_1=\left( \begin{matrix} 1\\ 1\end{matrix} \right) \]

当\(\lambda_1\)=4时，对应的特征向量应满足

\[\left( \begin{matrix} 3-4 & -1\\ -1 & 3-4\end{matrix} \right)\left( \begin{matrix} x_1\\ x_2\end{matrix} \right)=\left( \begin{matrix} 0\\ 0\end{matrix} \right) \]

解得\(x_1=- x_2\), 所以特征向量可取为

\[p_1=\left( \begin{matrix} -1\\ 1\end{matrix} \right) \]

4.特征向量和特征值的性质

对于常用的性质做以下总结：

1. 求特征值的矩阵A必须为方阵
2. n阶方阵A 有n个特征值
3. 若\(p_i\)是矩阵A对应于特征值\(\lambda_i\)的特征向量，则特征向量的\(kp_i\)也是对应于特征值\(\lambda_i\)的特征向量
4. 一个方阵的一组特征向量是一组正交向量

5.特征向量和特征值的应用

我们从前面了解到一个矩阵其实就是一个线性变换。特征值所对应的特征向量就是描述这个矩阵变化方向，我们通过特征值分解得到的前N个特征向量，就对应了这个矩阵最主要的N个变化方向。可以近似这个矩阵（变换）。也就提取这个矩阵最重要的特征。