【机器学习】集成学习中方差和偏差的理解
一个集成模型(f)在未知数据集(D)上的泛化误差E(f;D),由方差(var),偏差(bais)和噪声(ε)共同决定。
1. 方差和偏差的基本概念
观察下面的图像,每个点就是集成算法中的一个基评估器产生的预测值。红色虚线代表着这些预测值的均值,
而蓝色的线代表着数据本来的面貌。

-
偏差
模型的预测值与真实值之间的差异,即每一个红点到蓝线的距离。在集成算法中,每个基评估器都会有
自己的偏差,集成评估器的偏差是所有基评估器偏差的均值。模型越精确,偏差越低。 -
方差
反映的是模型每一次输出结果与模型预测值的平均水平之间的误差,即每一个红点到红色虚线的距离,
衡量模型的稳定性。模型越稳定,方差越低。
其中偏差衡量模型是否预测得准确,偏差越小,模型越“准”;而方差衡量模型每次预测的结果是否接近,即是说方差越小,模型越“稳”;噪声是机器学习无法干涉的部分。
一个好的模型,要对大多数未知数据都预测得”准“又”稳“。即是说,当偏差和方差都很低的时候,模型的泛化误差就小,在未知数据上的准确率就高。

2. 方差和偏差的关系
通常来说,方差和偏差有一个很大,泛化误差都会很大。然而,方差和偏差是此消彼长的,不可能同时达到最小
值。这个要怎么理解呢?来看看下面这张图:
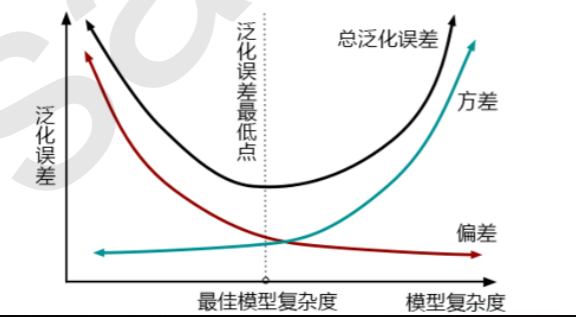
从图上可以看出,模型复杂度大的时候,方差高,偏差低。由于复杂度大,模型在训练集上尽量学了更多的细节,所以预测的准,偏差低。但这可能会导致过拟合,使得模型在不同数据上表现不稳定,模型泛化性差,所以方差就大。
相对的,复杂度低的时候,方差低,偏差高。由于复杂度低,模型在训练集上学习的比较简单,无法在某一类或者某一组数据上达成很高的准确度,所以偏差就会大。但是模型会预测得比较稳定。
所以,我们调参的目标是,达到方差和偏差的完美平衡。虽然方差和偏差不能同时达到最小值,但他们组成的泛化误差却可以有一个最低点,而我们就是要寻找这个最低点。对复杂度大的模型,要降低方差,对相对简单的模型,要降低偏差。
举个例子,比如随机森林的基评估器都拥有较低的偏差和较高的方差,因为决策树本身是预测比较”准“,比较容易过拟合的模型,装袋法本身也要求基分类器的准确率必须要有50%以上。所以以随机森林为代表的装袋法的训练过程旨在降低方差,即降低模型复杂度,所以随机森林参数的默认设定都是假设模型本身在泛化误差最低点的右边。所以,我们在降低复杂度的时候,本质其实是在降低随机森林的方差,随机森林所有的参数,也都是朝着降低方差的目标去。有了这一层理解,我们对复杂度和泛化误差的理解就更上一层楼了,对于我们调参,也有了更大的帮助。


