SVM从入门到精通
参考：https://blog.csdn.net/v_july_v/article/details/7624837
SVM定义
支持向量机，是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。
分类标准的起源：Logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。因此，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为是属于y=1的概率。
假设函数：
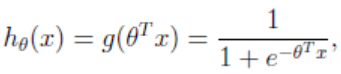
其中x是n维特征向量，函数g就是logistic函数，取值范围(0,1)
对新的特征做预测时，只需要求h(x)，如果大于0.5就是y=1的类，反之就是y=0
h(x)只跟 $\theta^Tx$有关，$\theta^Tx$>0, 那么h(x)>0.5, g(z)只是用来映射的，真实的类别决定权还在于$\theta^Tx$.
当$\theta^Tx>>0$,h(x)=1, Logistic回归就是要学习得到$\theta$,使得正例的特征远大于0，负例的特征远小于0，而且要在全部训练实例上达到这个目标
其中$\theta^Tx$中有一项是$\theta_0$,就等价于线性分类器中的b
除了y由y=0变成y=-1外，线性分类函数跟logistic回归的形式化表示没区别。
线性分类器
当f(x) = 0, 表示x是位于超平面上的点，当f(x)>0 的点对应于y=1的数据点， f(x)<0的点对应于y=-1的点
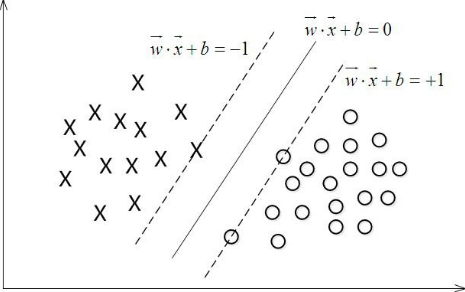
换言之，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1。
接下来的问题是，如何确定这个超平面呢？从直观上而言，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以，得寻找有着最大间隔的超平面。
函数间隔Functional margin与几何间隔Geometrical margin
函数间隔定义
$\gamma=y(w^Tx+b)=yf(x)$这是对于单个样本到超平面的函数间隔
总体函数间隔定义如下：
$\hat{\gamma}=min \gamma_i$ 所以样本点中离超平面最近的距离作为最终的函数间隔
但是这样定义有问题，如果成比例改变W,b，比如扩大为2倍，那么函数间隔也将扩大2倍(此时超平面没有改变)、
所以我们要对法向量w加些约束条件，从而引出真正定义点到超平面的距离--几何间隔
