C++ STL：lower_bound与upper_bound实现

lower_bound

lower_bound(begin, end, target)用来查找一个已排序的序列中[begin, end)第一个大于等于target的元素index。数组A如下：

value： 1, 2, 2, 3, 4, 5, 5, 6, 7

index： 0, 1, 2, 3, 4, 5, 6, 7, 8

这样的一个序列，如果查找5的lower_bound，返回的应该是第一个5即A[5]。下面是摘自cplusplus.com上的lower_bound代码

template <class ForwardIterator, class T>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last, const T& val)
{
  ForwardIterator it;
  iterator_traits<ForwardIterator>::difference_type count, step;
  count = distance(first,last);
  while (count>0)
  {
    it = first; step=count/2; advance (it,step);
    if (*it < val) {                 // or: if (comp(*it,val)), for version (2)
      first  = ++it;
      count -= step+1;
    }
    else count = step;
  }
  return first;
}

如果搜索对象只是数组的话还可以再简化一点：

count = last - start;
while (count > 0) {
    step = count/2;
    int* it = first + step;
    if (*it < target) {
        count = count - (step + 1);
        first = it + 1;
    } else {
        count=step;
    }
}
return first;

 基本情况： 当输入只有一个元素时，而该元素不是要查找的元素时返回last，即该元素的后一个位置

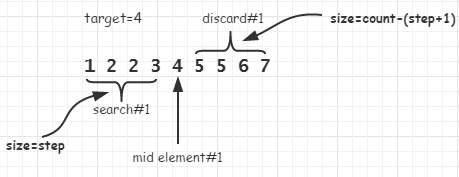
case: target=4

当在上图中的数组中找4的lower_bound时，第一次*it取到的值是4，因为这不是简单的二分搜索，而是要返回第一大于等于查找元素的位置，所以搜索不能在此时结束。但是可以确定5~7这一部分可以不用搜索了，因为当前至少有一个元素即*it是大于等于4了，因而缩小查找范围（count=step）。这个查找范围并不包括已找到的4，为什么是这样？分情况讨论：

1. 当前面的这个范围没有符合条件的数时，就会将范围最后的位置的后一位置返回，而此位置正好是4所在的位置（*it>= target时it所在的位置，它是符合查找条件的），其正好是lower_bound。

2. 当前面的这个方位含有符合条件的数时，此时当前的这个4就不是lower_bound，真正的lower_bound会在该区间内产生

case: target=5

当求5的lower_bound时，第一次找到中间元素时4，4<5，所以4和4前面的所有都不会含有5的lower_bound，因而下一次搜索只会在5~7这个区间进行，这个就和一个全新的问题一样了。

 

upper_bound

upper_bound用来在[begin, end)中找到第一个大于target的index

template <class ForwardIterator, class T>
  ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last, const T& val)
{
  ForwardIterator it;
  iterator_traits<ForwardIterator>::difference_type count, step;
  count = std::distance(first,last);
  while (count>0)
  {
    it = first; step=count/2; std::advance (it,step);
    if (!(val<*it))                 // or: if (!comp(val,*it)), for version (2)
      { first=++it; count-=step+1;  }
    else count=step;
  }
  return first;
}

简化版本：

lower_bound:

        int lo = 0, hi = n;
        // lower_bound
        while (lo < hi) {
            int mid = (lo + hi) / 2;
            if (A[mid] < target) {
                lo = mid + 1;
            } else {
                hi = mid;
            }
        }

        return lo;

upper_bound:

        lo = 0, hi = n;
        // upper_bound
        while (lo < hi) {
            int mid = (lo + hi) / 2;
            if (A[mid] <= target) {
                lo = mid + 1;
            } else {
                hi = mid;
            }
        }
        return lo;

 就在判断条件上多了个等号