再学二分图
增广路：从一个未匹配点出发，交替经过非匹配边、匹配边的路径，到达另一个未匹配点， 这一条路径叫做增广路。
以下省略绝对值符号，表示“集合大小”
- 最小点覆盖集 = 最大匹配数
- 最大点独立集 = 顶点总数 - 最大匹配数
- 最小边覆盖集 = 顶点总数 - 最大匹配数（无孤立点）
- DAG 最小路径覆盖 = 顶点总数 - 最大匹配数
二分图最少点边覆盖
对于一个已知的最大匹配，我们考虑从他出发求一组最小点覆盖集的方案
法 1
从左部所有非匹配点出发，做增广路，标记经过的所有点
我们选取左部点中所有未被标记点，与右部点中所有被标记的点，这就是一种方案
证明考虑增广路的性质，按两个端点是否匹配，把边分成 4 类进行讨论
法 2
考虑最小割：
- 新增源汇 \(s,t\)
- 二分图的边保留，边权为 \(+\infty\)
- \(s\) 向左部点连边权为 \(1\) 的边
- 右部点向 \(t\) 连边权为 \(1\) 的边
- 若一个点所连的边权为 \(1\) 的边被割，则该点要选
二分图最大独立集
方案：所有点扔去最小点覆盖的点
不可重最少路径覆盖问题
就是 DAG 的最小链覆盖
把原图每个点拆为左部点和右部点，若原图有一条有向边 \(u\to v\)，则在左部点中的点 \(u\) 连向右部点中的点 \(v\)，最大匹配指的是这个二分图的最大匹配
这里选中一条边，在原图中相当于合并两条路径
最多无路径点集
对第一问做传递闭包，就变成了第二问
对于第二问，由 Dilworth 定理，该图的最大独立集等于最小链覆盖，于是答案是好求的
最难的是如何给出方案：
- 先转二分图，在二分图上求出最大独立集：
- 新增源汇 \(s,t\)，每个点 \(u\) 拆为 \(p(u),q(u)\) 两个点
- \(s\) 向所有 \(p(u)\) 连边，所有 \(q(u)\) 向 \(t\) 连边
- 对于原图边 \((u,v)\)，连边 \(p(u)\to q(v)\)
- 若 \(p(u),q(u)\) 都在最大独立集里，则 \(u\) 在原图最大独立集中
证明：设 \(k\) 为最大匹配数，根据简单的抽屉原理，我们选择的点数 \(\ge n-k\)，而已知最小链覆盖 \(=n-k\) 等于最大独立集大小，所以对了。
棋盘博弈
删掉障碍点，对棋盘黑白染色得到一个二分图，二分图博弈经典结论：
- 规则：两人轮流沿边行动，不允许重复访问节点，无法移动者输。
- 结论：起点 \(u\) 是先手必胜的当且仅当 \(u\) 在所有最大匹配上。（自己推根本推不出来 QAQ）
证明：
- 必要性：若存在最大匹配不含 \(u\)，先手每次要么走到匹配点上（不然找到了一条增广路），要么无路可走，后手只需每次走到与当前点相匹配的点即可
- 充分性：当 \(u\) 在所有最大匹配上时，我们任取最大匹配，先手将 \(u\) 移动到匹配点，后手每次要么走到匹配点上（不然找到了一个不含起点的最大匹配），要么无路可走
判断方法：
- 删掉起点 \(u\)，再跑一遍最大匹配，若大小不变，则 \(u\) 是非必须点，则先手必败，否则先手必胜
- 跑最大流，若 \(u\) 在最大匹配中，且残量网络中 \(S\) 无法到达 \(u\)，则 \(u\) 是必须点，先手必胜，否则先手必败
第二种方法，正确性在于此时无法退流得到新的不含 \(u\) 的最大流方案
半最大独立集
一个一个连通块的处理
若不是二分图，即存在奇环，考虑全赋 0.5 是最优的
否则，求出最小点覆盖的点集，令该点集的点为 1，其余点为 0 是最优的
打副本
Gym 104090H
第二问的修改是不影响第一问的，先算第一问
首先一组内包含 4 种人：\(\texttt{D}\) 职业、\(\texttt{S}\) 职业、\(\texttt{B}\) 职业、\(\texttt{D}\) 或 \(\texttt{S}\) 灵活选择的职业
首先二分答案 \(k\)，然后可以最大流：
- 建点 \(s,t\)，7 个左部点 \(p_{\texttt{D}},p_{\texttt{S}},p_{\texttt{B}},p_{\texttt{DS}},p_{\texttt{DB}},p_{\texttt{SB}},p_{\texttt{DSB}}\) 分别表示 7 种人，4 个右部点 \(q_{\texttt{D}},q_{\texttt{S}},q_{\texttt{B}},q_{\texttt{D/S}}\) 表示担任组内哪个职业
- \(\forall u\in\) 左部点，设有 \(x\) 个人是 \(u\) 类人，\(s\to u\) 连容量为 \(x\) 的边
- \(\forall v\in\) 右部点，\(v\to t\) 连容量为 \(k\) 的边，表示需要这么多人
- \(\forall u\in\) 左部点，若 \(u\) 种类包含 \(\texttt{D}\)，连边 \(u\to q_{\texttt{D}},u\to q_{\texttt{D/S}}\)，若包含 \(\texttt{B}\)，连边 \(u\to q_{\texttt{B}}\)，以此类推，容量都为 \(+\infty\)
- 跑最大流，若跑满 \(4k\) 个人则有解；
- 或者使用霍尔定理，可以不用二分 \(O(2^4)\) 解决：\(Ans=\min_S\left\lfloor\frac{|N(S)|}{|S|}\right\rfloor\)
然后考虑第二问：
首先按成本对选手排序，最初这些选手全被选，每次选择可能可以不选的成本最高的选手，尝试取消他：
- 若不可能用剩下的人组成足够的小队，则该选手必须被选
- 若可能用剩下的人组成足够的小队，那就取消他
这样，设 \(d\) 类选手选了 \(\text{sz}(d)\) 个，其一定选的是成本最小的前 \(\text{sz}(d)\) 个
最后考虑如何进行修改 \((x,y)\)：
- 维护 7 个 multiset 存 7 种类型的未选人员的成本集合，再维护 7 个 multiset 存 7 种类型的已选人员的成本集合
- 若最优策略产生变化，可能有这几种情况：
- 若 \(x\) 没被选，而修改后会 \(\le\) 已选的最大值，可以尝试用他去替换某个类型已选的最大值
- 若 \(x\) 已被选，而修改后会 \(>\) 已选的最大值，可以尝试用某个类型未选的最小值去替换他
\(O(q\log n)\)
矩阵归零
设第 \(i\) 行减少量为 \(A_i\)，第 \(i\) 列减少量为 \(B_i\)（可以为负）
那么最终操作数为 \(\sum c_{i,j}-(n-1)(\sum A_i+\sum B_i)\)，注意单点只能减，所以要求 \(A_i+B_j\le c_{i,j}=|a_i-b_j|\) 情况下 \(\sum A_i+\sum B_i\) 最大。
把 \(A_i,B_i\) 取反，问题变成要求 \(A_i+B_j\ge-c_{i,j}\) 情况下 \(\sum A_i+\sum B_i\) 最小。
火速写出规划形式：
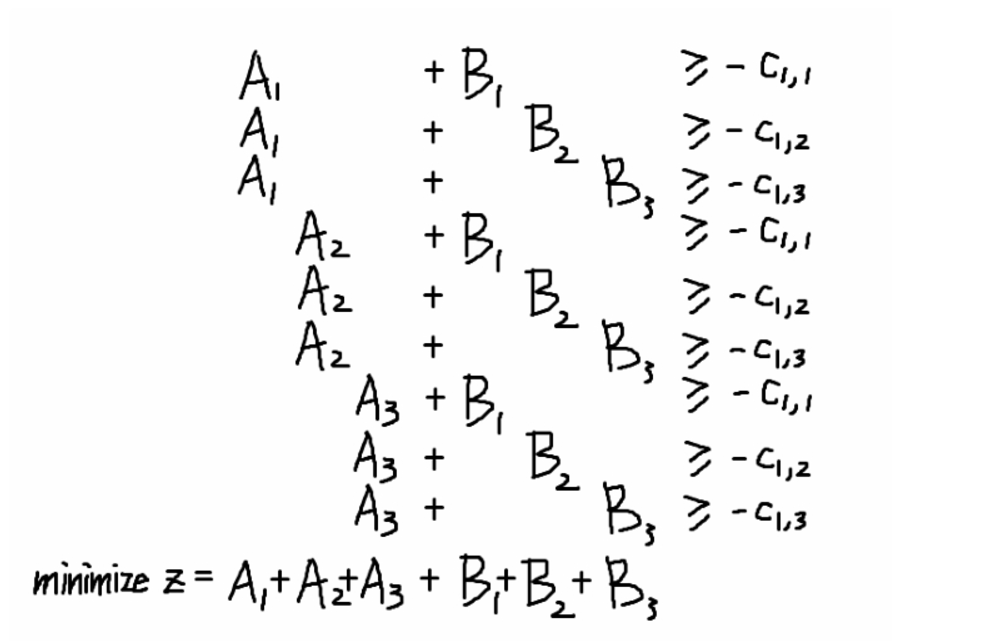
光速写出对偶问题：
直接赋予实际意义：\(x_{u,v}\) 表示一条左部点 \(u\) 连向右部点 \(v\) 的边是否被选入匹配，\(-c_{u,v}\) 表示该边的权值，求的是最大权完美匹配
很对啊！
问题变成让 \(a,b\) 两两匹配，使得差的绝对值之和最小
可以直接贪心：\(a,b\) 分别排序，然后对应位置匹配即可。
配对 1
LOJ 6062
令 \(b_i\gets h-b_i\)，再把 \(b\) 从大到小排序，单次判可以让 \(a\) 从大到小排序，若每个 \(a_i\ge b_i\) 则满足。
进行一步充要的转化：若对于每个 \(i\) 都有 \(\ge i\) 个 \(a_j\) 不小于 \(b_i\)，则满足
考虑直接线段树维护每个值有多少 \(a_i\) 大于等于他：
先给 \(a,b\) 离散化，初始 \(b_i\) 位置设为 \(-i\)，每加入一个 \(a_i\) 就令 \([1..a_i]\) 加一，问全局最小值是否 \(\ge 0\) 即可
若有多个相同的 \(b_i\)，取其中最大的 \(i\) 减就行了
配对 2
膜 include_c，他跟我讲的怎么做
首先转化条件，相当于左边 \(i\) 向右边 \((a_i-b_i)\bmod n\) 和 \((a_i+b_i)\bmod n\) 连边
也就是每个女生度数 \(\le 2\)（当时就做到这里。。。）
于是把每个男生看成一个点，每个女生看成一条边，连接她能选择的两个男生
这题就相当于，你要给这些边定向，要求最终每个点的入度 \(\le 1\)，且收益最大
发现如果要有解，一个连通块要么长成一棵树（一个点入度为 \(0\)），要么长成一棵基环树（没有点入度为 \(0\)）
于是讨论：
基环树：一定是外向地定向，所以只有两种情况，要么环上顺时针定向，要么环上逆时针定向，这个非常容易动态维护。
树：这个比较复杂，首先答案一定是选一个根，然后向外一层层定向
所以考虑换根，记 \(f(u)\) 为 \(u\) 点答案，你发现一条边的修改，可以看成对 \(f\) 的区间加
所以用一个线段树维护
\(O(n\log n)\)，有点难写
idea：一个点度数 \(\le 2\) 时可以尝试化点为边
Code
#include <bits/stdc++.h>
using namespace std;
#define rep(i, j, k) for (int i = (j); i <= (k); ++i)
#define reo(i, j, k) for (int i = (j); i >= (k); --i)
typedef long long ll;
const int N = 1e6 + 10;
ll ans, a[N], b[N];
int n, m, T, q;
struct Edge {
int v, w, id;
};
struct edge {
int u, v, w;
} ee[N];
vector<Edge> G[N];
int bro[N];
int vis[N];
int tp, nodestk[N];
int stp, nowstk[N], estp, nestk[N];
int tot, cir[N];
int etot, cire[N];
int oncirn[N];
int tim1, dfn1[N];
int dep[N];
void DFS1(int u, int fa, int fe = 0) {
dfn1[u] = ++tim1, vis[u] = 1, nodestk[++tp] = u, nowstk[++stp] = u;
for (auto e : G[u]) {
int v = e.v;
if (!vis[v]) nestk[++estp] = e.id, DFS1(v, u, e.id), --estp;
else if ((v != fa || e.id != bro[fe]) && dfn1[v] <= dfn1[u]) {
int tmp = stp;
while (nowstk[tmp] != v) cir[++tot] = nowstk[tmp--];
cir[++tot] = v;
tmp = estp;
if (u != v) {
while (ee[nestk[tmp]].u != v) cire[++etot] = nestk[tmp--];
cire[++etot] = nestk[tmp--];
reverse(cire + 1, cire + etot + 1);
cire[++etot] = e.id;
} else {
cire[++etot] = e.id;
}
}
}
--stp;
}
void DFS2(int u, int fa) {
dep[u] = dep[fa] + 1;
for (auto e : G[u]) {
int v = e.v;
if (v != fa && !oncirn[v]) {
ans += e.w, DFS2(v, u);
}
}
}
int cirtot, zheng[N], fan[N];
int oncire[N];
int tim, dfn[N], sz[N], ontree[N];
ll all;
void DFS3(int u, int fa) {
dfn[u] = ++tim, sz[u] = 1, dep[u] = dep[fa] + 1;
for (auto e : G[u]) {
int v = e.v;
if (v != fa) {
DFS3(v, u), sz[u] += sz[v];
all += e.w;
}
}
}
ll F[N];
array<int, 2> arrange[N];
void DFS4(int u, int fa, ll res) {
F[dfn[u]] = res;
for (auto e : G[u]) {
int v = e.v;
if (v != fa) {
DFS4(v, u, res - e.w + ee[bro[e.id]].w);
}
}
}
void Solve(int rt) {
tp = tot = stp = etot = estp = 0;
DFS1(rt, 0);
vector<int> edges;
rep(i, 1, tp)
for (auto e : G[nodestk[i]]) edges.push_back(e.id);
sort(edges.begin(), edges.end());
if ((int)edges.size() != (tp - 1) * 2) {
rep(i, 1, tot) oncirn[cir[i]] = 1;
rep(i, 1, tot) DFS2(cir[i], 0);
++cirtot;
rep(i, 1, etot) {
int e = cire[i];
zheng[cirtot] += ee[e].w;
fan[cirtot] += ee[bro[e]].w;
oncire[e] = cirtot;
oncire[bro[e]] = -cirtot;
}
ans += max(zheng[cirtot], fan[cirtot]);
} else {
int L = tim + 1;
all = 0;
DFS3(rt, 0), DFS4(rt, 0, all);
int R = tim;
ll res = 0;
rep(i, 1, tp) {
int u = nodestk[i];
res = max(res, F[dfn[u]]);
arrange[u] = {L, R};
ontree[u] = 1;
}
ans += res;
}
}
#define lc (u << 1)
#define rc ((u << 1) | 1)
#define mid ((l + r) >> 1)
ll add[N << 2], mx[N << 2];
void up(int u) {
mx[u] = max(mx[lc], mx[rc]);
}
void Add(int u, ll v) {
mx[u] += v, add[u] += v;
}
void down(int u) {
if (add[u]) Add(lc, add[u]), Add(rc, add[u]), add[u] = 0;
}
void build(int u, int l, int r) {
if (l > r) return;
if (l == r) return (void)(mx[u] = F[l]);
build(lc, l, mid), build(rc, mid + 1, r), up(u);
}
void upd(int u, int l, int r, int x, int y, ll v) {
if (y < l || r < x || x > y) return;
if (x <= l && r <= y) return Add(u, v);
down(u), upd(lc, l, mid, x, y, v), upd(rc, mid + 1, r, x, y, v), up(u);
}
ll qry(int u, int l, int r, int x, int y) {
if (y < l || r < x || x > y) return (ll)-1e18;
if (x <= l && r <= y) return mx[u];
return down(u), max(qry(lc, l, mid, x, y), qry(rc, mid + 1, r, x, y));
}
#undef lc
#undef rc
#undef mid
void init() {
rep(i, 1, n)
if (!vis[i])
Solve(i);
build(1, 1, tim);
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
cin >> m >> n >> T;
rep(i, 1, m) cin >> a[i];
rep(i, 1, m) cin >> b[i];
int tmp = 0;
rep(i, 1, m) {
int u = (a[i] - b[i] + n) % n + 1, v = (a[i] + b[i]) % n + 1, w;
if (u < v) swap(u, v);
cin >> w, ++tmp;
G[u].push_back({v, w, tmp}), ee[tmp] = {u, v, w}, bro[tmp] = tmp;
if (u != v) cin >> w, ++tmp, G[v].push_back({u, w, tmp}), ee[tmp] = {v, u, w}, bro[tmp - 1] = tmp, bro[tmp] = tmp - 1;
}
init();
cout << ans << '\n';
cin >> q;
while (q--) {
int x, v;
cin >> x >> v;
x -= ans * T, v -= ans * T;
if (oncire[x] != 0) {
int cirid = abs(oncire[x]);
int delta = v - ee[x].w;
ans -= max(zheng[cirid], fan[cirid]);
if (ee[x].u != ee[x].v) {
(oncire[x] > 0 ? zheng[cirid] : fan[cirid]) += delta;
} else {
zheng[cirid] += delta, fan[cirid] += delta;
}
ans += max(zheng[cirid], fan[cirid]);
ee[x].w = v;
}
else if (ontree[ee[x].u]) {
int U = ee[x].u, V = ee[x].v;
int l = arrange[U][0], r = arrange[U][1];
int p = dep[U] < dep[V] ? V : U;
int delta = v - ee[x].w;
ans -= qry(1, 1, tim, l, r);
if (dep[U] > dep[V]) {
upd(1, 1, tim, dfn[p], dfn[p] + sz[p] - 1, delta);
}
else {
upd(1, 1, tim, l, r, delta);
upd(1, 1, tim, dfn[p], dfn[p] + sz[p] - 1, -delta);
}
ans += qry(1, 1, tim, l, r);
ee[x].w = v;
}
else {
int U = ee[x].u, V = ee[x].v;
if (dep[U] < dep[V]) {
ans = ans - ee[x].w + v;
}
ee[x].w = v;
}
cout << ans << '\n';
}
return 0;
}
