简单萌萌哒 Top Tree(上)
前情提要(?
Top Cluster 分解与 Top Tree
情景导入
我们总是想要以一种合适的方式对树进行划分,但是对于菊花图而言,基于点的划分总是不合适的,这启发我们基于边进行划分。事实上可以证明,基于边的划分总是可行的。
Top Cluster 分解就是一种基于边的划分方式,下面我们来介绍他。
簇、簇操作、树的簇表示法
定义:
- 一个簇可以表示为一个三元组 ,其中 为树的节点,称为簇的界点(或端点), 为一个边集,表示该簇包含的边,路径 称为簇路径。
- 对于树的一条边 , 是一个簇。
- 对于簇 ,簇 ,记 。
- 对于簇 ,簇 ,记 。
其中 Rake 和 Compress 是树收缩的两种基本操作。形象的理解,一个簇可以看成一条边,Rake 就是把一条边“拍”到另一条边上,Compress 就是把两条边“拼”成一条;Rake 是去掉一度点,Compress 是去掉二度点。如下图:
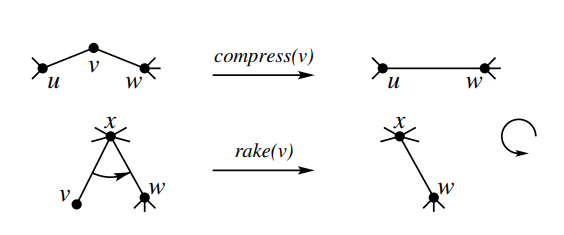
显然,一棵树可以不断地进行这两种操作来合并为一个簇。一种方法是,不断地 Rake 来剥掉叶子。
进行若干次收缩后,用簇路径来代替原来的边,可以得到一个树形结构(下图左),称为收缩树;还可以得到一棵二叉树(下图右),每个点代表一个簇,其两个儿子表示 Compress 或 Rake 操作的两个簇。我们把这棵二叉树称为 Top Tree。每个叶子节点是一条边,称为基簇;其根节点表示整棵树的簇,称为根簇。
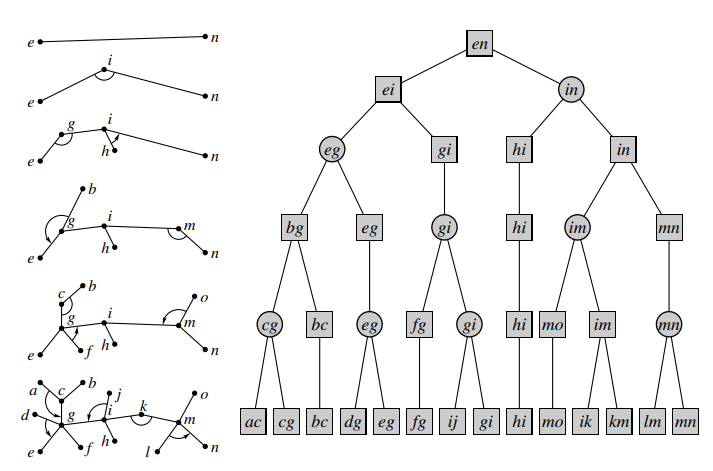
(右图:圆点:Rake 而来的点,称为 Rake 节点;方点:Compress 而来的点,称为 Compress 节点;点上的两个小写字母表示这个簇的界点)
基于重量平衡的静态 Top Tree
为了方便问题的解决,我们希望 Top Tree 的深度是 的。下面介绍一种构建方法:
首先注意到,簇的合并方式 与 轻重链剖分 有某种共性:Compress 相当于重链上 Pushup,Rake 相当于轻子树信息的合并。所以我们对原树进行轻重链剖分,DFS 地自底向上处理每条重链,并认为每个轻子树已经合并为一个簇。
对于重链上的每个点 ,把 的轻子树的簇 Rake 到边 ,这里需要分治地 Rake 保证深度不会太大,称这样操作形成的树为 Rake 树。
然后我们得到了排成一条链的簇,同样分治地 Compress 这些簇来保证深度,称这样操作形成的树为 Compress 树。
显然,这样合并得到的 Top Tree 的深度为 。如何优化?
直接借用“全局平衡二叉树”的思想,在分治 Compress 或 Rake 时按簇的大小选择带权中点作为分治中点,这样向上跳两次子树大小至少翻倍,于是 Top Tree 的深度就为 了。
按这样构建出的 Top Tree 拥有一些很好的性质:
- 所有簇的界点都有祖先关系。
- 簇的上界点为整个簇中深度最小的点。
- Compress 树的中序遍历是按照深度升序遍历,从上到下。
Top Tree 是关于边的划分,而我们时常需要维护点的信息,为此我们定义:一个簇包含其连通块中的所有除上界点以外的点,这样每个点在每一层中最多属于一个簇。根节点可以加入一条额外边或特殊考虑来解决。
簇与 Top Tree 的性质
我们约定,如果没有特殊说明,“簇”都指的是 Top Tree 上的簇。下面列出一些比较显然但是重要的性质:
- 根据定义,簇中只有不超过 2 个点与外部点邻接,这两个点一定是界点。
- 任意两个簇,要么相互包含,要么两者的交最多只有一个点,且这个点是两个簇的共有的界点。
- 一个不是基簇的簇,其两个子簇恰好有一个共有的界点,我们称其为该簇的中心点。
- 从外部经过一个簇的路径必定经过该簇的界点。特别地,如果这个路径完全跨过了该簇,那么该簇的簇路径是其的一个子路径。
Top Tree 是一棵二叉树,每个点代表一个簇,父亲由儿子合并而来,叶子是一条条边的基簇。
Top Tree 的结构在某种意义上类似于线段树:
- 线段树的每个节点是一个区间,最多只有两端与外部邻接,而 Top Tree 的每个节点是一个簇,最多只有两端与外部邻接;(这也是他的信息可快速合并的原因之一)
- 他们都维护子树信息并,是一种二叉分治结构,支持分治、二分,是 Leafy 的;
- 他们的树高都应该是 ;
- ……
所以我们可以将 Top Tree 直观理解为树上的线段树。
Top Tree 的实现与维护
在讲 Top Tree 的实际应用前,我们先讲一下如何实现和维护 Top Tree。
一些可以简单地快速合并的树上信息的例子
-
簇内点数 :
-
簇路径长度 :
-
上/下端点到簇内最远点距离 :(以上端点为例)
-
簇内直径大小 :
静态 Top Tree 的实现
首先定义 Cluster 表示一个簇的信息,其中 u 是上界点,v 是下界点。然后有 Rake 和 Compress 两个基本操作。
struct Cluster { int u, v; int dis; // 簇路径长度 int siz; // 簇内点数 }; Cluster Rake(const Cluster &x, const Cluster &y) { return { x.u, x.v, x.dis, x.siz + y.siz }; } Cluster Compress(const Cluster &x, const Cluster &y) { return { x.u, y.v, x.dis + y.dis, x.siz + y.siz }; }
然后定义 Node 类,表示 Top Tree 上的点,并实现一个对 Cluster 序列带权分治建树的函数 DAC
struct Node { int ch[2], fa, type; // type 0/1/2 分别为 base/rake/compress Cluster x; int &operator[](int x) { return ch[x]; } } f[1000005]; int cnt; void Pushup(int x) { if (f[x].type == 0) return; f[x].x = (f[x].type == 1 ? Rake : Compress)(f[f[x][0]].x, f[f[x][1]].x); } int Merge(int u, int v, int type) { f[++cnt] = { { u, v }, 0, type }; f[u].fa = f[v].fa = cnt; Pushup(cnt); return cnt; } int DAC(vector<int> &vec, int l, int r, int type) { if (l == r) return vec[l]; int sum = 0; for (int i = l; i <= r; ++i) sum += f[vec[i]].x.siz; int mid = r - 1; for (int i = l, cur = 0; i <= r; ++i) { cur += f[vec[i]].x.siz; if (cur * 2 >= sum) { mid = i; break; } } return Merge(DAC(vec, l, mid, type), DAC(vec, mid + 1, r, type), type); }
最后是整棵树的建树过程:
int idf[100005]; // (u, fa[u]) 这个基簇的编号 int siz[100005], fa[100005], son[100005]; vector<int> G[100005]; void DFS1(int u, int fth = 0) { siz[u] = 1, fa[u] = fth; for (int v : G[u]) { if (v == fth) continue; f[++cnt] = { { 0, 0 }, 0, 0, { u, v, 1, 1 } }; DFS1(v, u), siz[u] += siz[v]; if (siz[v] > siz[son[u]]) son[u] = v; } } int Build(int top) { vector<int> cpr; if (idf[top]) cpr.push_back(idf[top]); for (int u = top; son[u]; u = son[u]) { vector<int> rke; // 先把轻子树全部合并起来 for (int v : G[u]) if (v != son[u] && v != fa[u]) rke.push_back(Build(v)); if (!rke.empty()) { // 分治 rake 其他子树,最后 rake 到重儿子上 cpr.push_back(Merge(idf[son[u]], DAC(rke, 0, (int)rke.size() - 1, 1), 1)); } else { cpr.push_back(idf[son[u]]); } } return DAC(cpr, 0, (int)cpr.size() - 1, 2); }
这样,我们就初步实现了一棵静态 Top Tree。
动态 Top Tree 的维护
动态 Top Tree,就是支持一些动态操作的 Top Tree:
- :将根簇变为簇路径为 的一个簇。
- :在 间连边。
- :断开 之间的边。
有一些数据结构可以实现动态 Top Tree,其中最好写实用的就是 SATT(Self-Adjusting Top Tree),接下来我们来介绍他。
注:这里的 SATT 不同于原论文版本,但是思想是相同的。
SATT 的组合结构
首先,静态 Top Tree 本质上是在描述一个链分治的过程,也就是每次选择一条重链,把剩下的部分递归分解,然后分治把轻儿子合并到重边上(对应 Rake Tree),再分治合并重链。(对应 Compress Tree)
接下来,我们把原本静态 Top Tree 的结构用一棵三叉树的结构替代:
- 对于每个 Compress 节点,其左右儿子不变仍然描述重链的分治树,而中儿子挂上一棵 Rake Tree,表示先把这棵 Rake Tree 合并(Rake)到这个 Compress 节点上。
- 对于每个 Rake 节点,它的左右儿子仍然描述分治 Rake 的过程,而中儿子挂上一棵 Compress Tree,表示把左右儿子 Rake 到中儿子上。
这就得到了 SATT 的实际结构。
注意,这里的分治过程是非 Leafy 的,也就是 Compress 节点本身就代表一个点,Rake 节点本身代表它的中儿子。
整理一下:
- SATT 是一棵三叉树,每个节点代表一个簇。
- 有两种节点:Compress 节点或 Rake 节点
- 对于 Compress 节点:
- 它的左右儿子是 Compress 节点,中儿子是 Rake 节点;
- 表示它所代表的簇,由它自身所代表的节点与中儿子 Rake,再与左右儿子 Compress 得到;
- 它与它的左右儿子描述了一条链的分治树。
- 对于 Rake 节点:
- 它的左右儿子是 Rake 节点,中儿子是 Compress 节点;
- 表示它所代表的簇,由中儿子分别与左右儿子 Rake 得到;
- 它与它的儿子描述了分治 Rake 的过程。
- 一个 Rake 节点一定有一个中儿子。
这一结构看起来很像平衡树维护轻儿子的 LCT,或者非 Leafy 的 AAAT(前情提要 中有):一条实链被一棵 Compress Tree 维护,然后轻儿子被 Rake Tree 挂在下面。
附一张图:
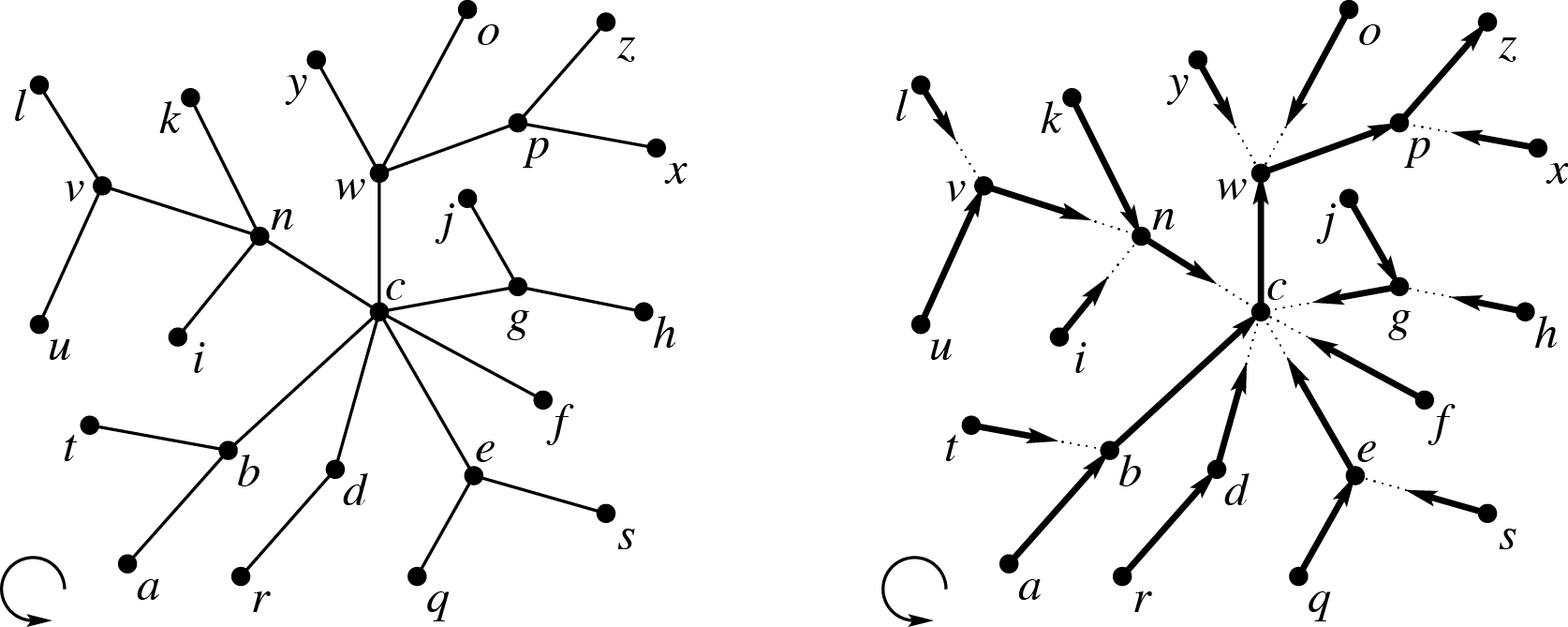
一个大家经常搞不清楚的地方是,点是如何在 SATT 中维护的。
我们对簇的定义稍加修改,即可严格支持点的维护:
- 一个簇可以表示为一个四元组 ,其中 为簇的界点(或端点), 为该簇包含的边集, 为该簇包含的点集。
- 对于树的一条边 , 是一个簇。
- 对于树的一个点 , 是一个簇。
- 对于簇 ,簇 ,记 。
- 对于簇 ,簇 ,记 。
这样,我们只需把一个单点所组成的簇,作为 Compress 节点加入 SATT,点的信息放在它对应的 Compress 节点上加入即可。
注意到无论一个簇的界点是哪个点,是否被包含在这个簇中,都不影响我们维护信息。
下图不包含所有情况,只是举例而已。
这样定义的簇应该形如:

SATT 中一次合并得到 Compress / Rake 节点,在原树中应该像这样:

(图中方点表示 Compress 节点,圆点表示 Rake 节点,下同)
SATT 的动态操作
注意到重链剖分、LCT 之间的关系,与静态 Top Tree、SATT 之间的关系比较类似:
- LCT 本质上是把重链剖分的线段树变为可旋转、可加入删除一条实链的 Splay(虚实转化),实现了动态化。
- 那么 Top Tree 是否可以支持旋转、插入删除一个簇呢?
Rotate & Splay
注意到,在保持中儿子不变的情况下,不管是 Rake Tree 还是 Compress Tree 我们都只关心它的左右儿子的中序遍历,而非树的具体形态,这意味着它是支持旋转的:
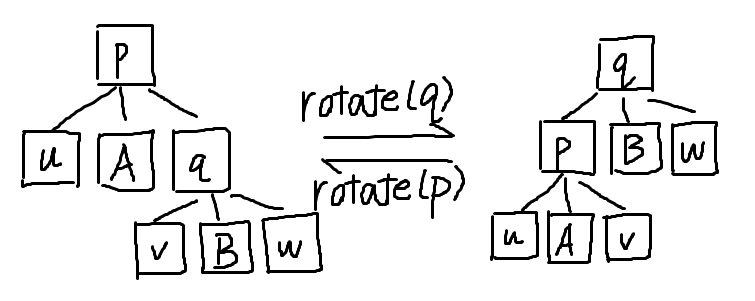
那么就自然可以 Splay 了,这个东西与 LCT 的是相同的。
Splice
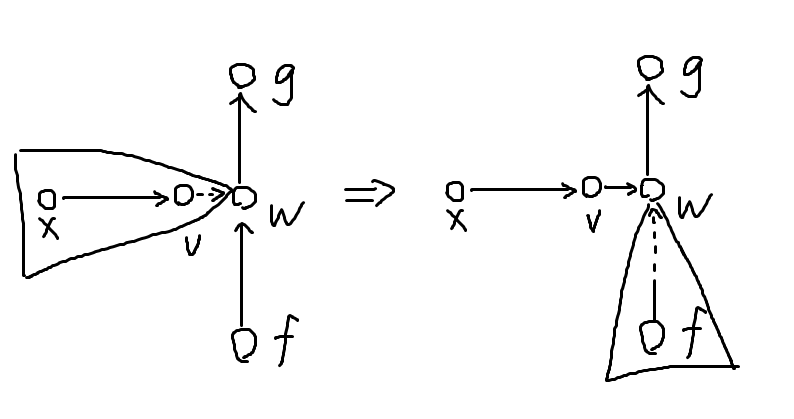
在讨论 Access 操作之前,我们先介绍一个操作 ,表示将簇 (一定是 Rake 节点)的中儿子插入到它父亲(一定是 Compress 节点)的簇上,如下图:

先把 旋到它所在 Rake Tree 的根,设其父亲为 ,其中儿子为 ,容易知道 和 一定是 Compress 节点。然后把 旋到这棵 Compress Tree 的根。
我们希望 成为 的右儿子。那么讨论:
- 若 有右儿子,直接让 与 的右儿子交换即可。
- 否则,我们让 挂到 的右儿子上,此时 失去了中儿子,作为 Rake 节点已经不合法,那么我们将 的左右子树做 Splay 合并后删去 即可。
最后还要对必要的点 Pushup。

Access
表示让点 与原树的根节点组成根簇的界点。
有了 操作后其实就简单了:
首先 。我们希望 成为当前簇的一个界点,即此时在 Compress Tree 中 没有右儿子。
- 若 有右儿子,直接新建点 然后把 的中儿子、右儿子分别挂到 的左儿子、中儿子上,再令 成为 的中儿子即可。
- 然后一直 、 直到 成为根。
最后 Splay 一下原始的 。
第一步称为 Local Splay,如下图:

第二步称为 Global Splay,如图:
这样一直重复。
Makeroot
显然,先 再翻转 子树即可。翻转标记只在 Compress 节点之间下传即可。
Expose
将根簇的簇路径变为 。
显然,先 再 即可。
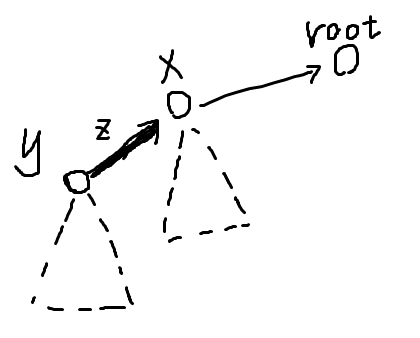
Link
表示连边 ,这条边在 SATT 上编号为 。
先 ,再 ,再把 挂到 的右儿子、 挂到 的左儿子即可。
Cut
先 ,再删除 的右儿子,最后断开 即可。
如图:

以上就是 SATT 的基本操作。
时间复杂度证明:不会。
SATT 维护其他信息主要是通过修改 函数,或非局部搜索来求。
SATT 的代码实现
以 Sone1 为例,我们来介绍如何实现 SATT。
这题要求我们维护:
- 换根,换父亲
- 子树 / 链的点权
- 子树 / 链 加 / 赋值
对于链,直接 就是所求;对于子树,考虑 然后 以及其中子树就是所求。
所以可以维护这些信息:
- 簇路径的 标记
- 簇内簇路径以外部分的 标记
- 簇路径的 信息
- 簇内簇路径以外部分的 信息
而原本 SATT 要求我们维护:
- 该点权值
- 这个点的三个儿子和父亲
- 子树翻转标记
我个人还习惯维护 表示这个子树内的最左 / 最右点。
那么我们首先实现 Tag 和 Dat 类:
const int inf = 1e9; struct Tag { int k, b; Tag(int k = 1, int b = 0) : k(k), b(b) {} bool NE() { return k != 1 || b != 0; } }; struct Dat { int siz, min, max, sum; Dat(int siz = 0, int min = inf, int max = -inf, int sum = 0) : siz(siz), min(min), max(max), sum(sum) {} }; Tag operator+ (const Tag &x, const Tag &y) { return { x.k * y.k, x.b * y.k + y.b }; } int operator+ (const int &x, const Tag &y) { return x * y.k + y.b; } Dat operator+ (const Dat &x, const Tag &y) { return { x.siz, x.min == inf ? inf : x.min + y, x.max == -inf ? -inf : x.max + y, x.sum * y.k + x.siz * y.b }; } Dat operator+ (const Dat &x, const Dat &y) { return { x.siz + y.siz, min(x.min, y.min), max(x.max, y.max), x.sum + y.sum }; }
然后定义 Node 类,以及一些基本函数。
struct Node { int fa, ch[3]; // 0/1/2 表示 左/右/中 儿子 int lef, rig, val; // 子树内最左点、最右点,该点权值 Dat pat, sub; // 簇路径信息,簇路径以外部分信息 Tag tpa, tsu; // 簇路径标记,簇路径以外部分标记 bool rev; // 子树翻转标记 void Clear() { fa = ch[0] = ch[1] = ch[2] = lef = rig = val = 0; rev = false, pat = sub = Dat(), tpa = tsu = Tag(); } } f[1000005]; int cnt, tp, st[1000005]; // 点数,内存回收 int &ls(int x) { return f[x].ch[0]; } int &ms(int x) { return f[x].ch[2]; } int &rs(int x) { return f[x].ch[1]; } int &fa(int x) { return f[x].fa; } int &lef(int x) { return f[x].lef; } int &rig(int x) { return f[x].rig; } int NewNode() { return tp ? st[tp--] : ++cnt; }
然后是一些基本的操作函数:
// 找出 x 是它父亲的哪个儿子 int Get(int x) { return ls(fa(x)) == x ? 0 : (rs(fa(x)) == x ? 1 : 2); } // 判断 x 不在当前 Compress Tree / Rake Tree 的根 bool Nrt(int x) { return ls(fa(x)) == x || rs(fa(x)) == x; } // 把 x 挂到 fx 的 t 儿子上 void Set(int x, int fx, int t) { if (x) f[fa(x)].ch[Get(x)] = 0, fa(x) = fx; f[fx].ch[t] = x; } // 删除点 x void Clear(int x) { f[st[++tp] = x].Clear(); } // 对 x 施加翻转标记 void Rev(int x) { swap(ls(x), rs(x)), swap(lef(x), rig(x)), f[x].rev ^= 1; } // 对 x 施加簇路径标记 void PathTag(int x, Tag w) { f[x].val = f[x].val + w; f[x].pat = f[x].pat + w; f[x].tpa = f[x].tpa + w; } // 对 x 施加簇路径以外部分标记 void SubTag(int x, Tag w) { f[x].sub = f[x].sub + w; f[x].tsu = f[x].tsu + w; }
然后是 Pushdown 与 Pushup 函数
void Down(int x, int t) { // t = 0 表示 x 是 Compress 节点,t = 1 表示 x 是 Rake 节点,下同 if (!t) { if (f[x].rev) { // 翻转标记只在 Compress 节点之间下传 Rev(ls(x)); Rev(rs(x)); f[x].rev = false; } if (f[x].tpa.NE()) { // 簇路径标记也只在当前 Compress Tree 中下传 PathTag(ls(x), f[x].tpa); PathTag(rs(x), f[x].tpa); f[x].tpa = Tag(); } if (f[x].tsu.NE()) { // 簇路径以外部分的标记,下传给所有儿子 SubTag(ls(x), f[x].tsu); SubTag(rs(x), f[x].tsu); SubTag(ms(x), f[x].tsu); f[x].tsu = Tag(); } } else { if (f[x].tsu.NE()) { // 对于 Rake 节点,直接下传即可 SubTag(ls(x), f[x].tsu); SubTag(rs(x), f[x].tsu); // 对于 Compress 节点,因为是修改整个簇,所以下传给两种标记 SubTag(ms(x), f[x].tsu); PathTag(ms(x), f[x].tsu); f[x].tsu = Tag(); } } } void Pushdown(int x, int t) { if (Nrt(x)) Pushdown(fa(x), t); Down(x, t); } void Pushup(int x, int t) { // 更新最左最右点 lef(x) = ls(x) ? lef(ls(x)) : x; rig(x) = rs(x) ? rig(rs(x)) : x; if (!t) { // 更新簇路径信息,也是 Compress Tree 的子树信息 f[x].pat = f[ls(x)].pat + Dat(1, f[x].val, f[x].val, f[x].val) + f[rs(x)].pat; // 更新非簇路径部分信息 f[x].sub = f[ls(x)].sub + f[ms(x)].sub + f[rs(x)].sub; } else { // 对于 Rake 节点,我们令它的 sub 维护整个簇的信息 f[x].sub = f[ls(x)].sub + f[rs(x)].sub + f[ms(x)].sub + f[ms(x)].pat; } }
然后实现 Rotate 和 Splay 函数:
void Rot(int x, int t) { int y = fa(x), z = fa(y), d = Get(x), p = f[x].ch[!d]; if (z) f[z].ch[Get(y)] = x; if (p) fa(p) = y; fa(x) = z, f[x].ch[!d] = y; fa(y) = x, f[y].ch[d] = p; Pushup(y, t), Pushup(x, t); } void Splay(int x, int t, int tar = 0) { // tar 表示把 x 旋到 tar 的儿子 for (Pushdown(x, t); Nrt(x) && fa(x) != tar; Rot(x, t)) if (Nrt(fa(x)) && fa(fa(x)) != tar) Rot(Get(x) == Get(fa(x)) ? fa(x) : x, t); }
然后是 Splice,我们再实现一个 Del 函数表示将没有中儿子的 Rake 节点删掉。
void Del(int x) { // x 是 Rake 节点 if (ls(x)) { // 将 ls 与 rs 做 Splay 合并 int y = rig(ls(x)); Splay(y, 1, x), Set(rs(x), y, 1); // 把 y 挂到 fa 的中儿子上并更新信息 Set(y, fa(x), 2); Pushup(y, 1), Pushup(fa(x), 0), Clear(x); } else { // 没有左儿子,直接把 rs 挂到 fa 的中儿子上 Set(rs(x), fa(x), 2), Pushup(fa(x), 0), Clear(x); } } void Splice(int x) { // x 是 Rake 节点 // 先把 x 旋到根,再把 fa 旋到根 Splay(x, 1); int y = fa(x); Splay(y, 0), Down(x, 1); // 这里 Down 是因为 Del 中要用到 ls 的 rig if (rs(y)) { // 交换 ms(x) 与 rs(fa) swap(fa(ms(x)), fa(rs(y))); swap(ms(x), rs(y)); Pushup(x, 1), Pushup(y, 0); } else { // 直接把 ms(x) 挂到 fa 的右儿子上,并删除没有中儿子的 x Set(ms(x), y, 1), Del(x); Pushup(y, 0); } }
然后是 Access。
void Access(int x) { // x 是 Compress 节点 // 让 x 成为当前簇的端点 Splay(x, 0); if (rs(x)) { // 把 ms, rs 分别挂到新点的 ls, ms 上 int y = NewNode(); Set(ms(x), y, 0); Set(rs(x), y, 2); // 把新点挂到 x 的中儿子上 Set(y, x, 2); Pushup(y, 1), Pushup(x, 0); } // 不断地 Splice 直到成为根 for (int y = x; fa(y); y = fa(y)) { Splice(fa(y)); } Splay(x, 0); /* 上面的 4 行可以改为: for (; fa(x); Splay(x, 0)) { Splice(fa(x)); } */ }
接下来是一些动态操作:
int rt; void Makert(int x) { // 让 x 成为根 Access(x), Rev(x); } int Find(int x) { // 找到 x 所在子树的根 return Access(x), lef(x); } void Split(int x, int y) { // 就是 Expose Makert(x), Access(y); } void MPath(int x, int y, Tag w) { // 路径修改 Split(x, y), PathTag(y, w); } void MSub(int x, Tag w) { // 子树修改 Split(rt, x), f[x].val = f[x].val + w, SubTag(ms(x), w), Pushup(x, 0); } Dat QPath(int x, int y) { // 路径查询 return Split(x, y), f[y].pat; } Dat QSub(int x) { // 子树查询 return Split(rt, x), f[ms(x)].sub + Dat(1, f[x].val, f[x].val, f[x].val); } void Link(int x, int y) { // 连接 x, y Access(x), Makert(y), Set(y, x, 1), Pushup(x, 0); } void Chgfa(int x, int y) { // 修改原树中 x 的父亲为 y if (x == rt || x == y) return; Split(rt, x); int p = rig(ls(x)); // x 的原来父亲 ls(x) = fa(ls(x)) = 0, Pushup(x, 0); // 断开原来 x 与 p 的边 if (Find(x) == Find(y)) Link(x, p); // x 与 y 连通,那么重连 x 与 p else Link(x, y); // 否则连接 x 与 y }
注意主函数中一开始要令 cnt = n。
完整代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int inf = 1e9; struct Tag { int k, b; Tag(int k = 1, int b = 0) : k(k), b(b) {} bool NE() { return k != 1 || b != 0; } }; struct Dat { int siz, min, max, sum; Dat(int siz = 0, int min = inf, int max = -inf, int sum = 0) : siz(siz), min(min), max(max), sum(sum) {} }; Tag operator+ (const Tag &x, const Tag &y) { return {x.k * y.k, x.b * y.k + y.b}; } int operator+ (const int &x, const Tag &y) { return x * y.k + y.b; } Dat operator+ (const Dat &x, const Tag &y) { return {x.siz, x.min == inf ? inf : x.min + y, x.max == -inf ? -inf : x.max + y, x.sum * y.k + x.siz * y.b}; } Dat operator+ (const Dat &x, const Dat &y) { return {x.siz + y.siz, min(x.min, y.min), max(x.max, y.max), x.sum + y.sum}; } struct Node { int fa, ch[3]; int lef, rig, val; Dat pat, sub; Tag tpa, tsu; bool rev; void Clear() { fa = ch[0] = ch[1] = ch[2] = lef = rig = val = 0; rev = false, pat = sub = Dat(), tpa = tsu = Tag(); } } f[1000005]; int cnt, tp, st[1000005]; int &ls(int x) { return f[x].ch[0]; } int &ms(int x) { return f[x].ch[2]; } int &rs(int x) { return f[x].ch[1]; } int &fa(int x) { return f[x].fa; } int &lef(int x) { return f[x].lef; } int &rig(int x) { return f[x].rig; } int NewNode() { return tp ? st[tp--] : ++cnt; } int Get(int x) { return ls(fa(x)) == x ? 0 : (rs(fa(x)) == x ? 1 : 2); } bool Nrt(int x) { return ls(fa(x)) == x || rs(fa(x)) == x; } void Set(int x, int fx, int t) { if (x) f[fa(x)].ch[Get(x)] = 0, fa(x) = fx; f[fx].ch[t] = x; } void Clear(int x) { f[x].Clear(), st[++tp] = x; } void Rev(int x) { swap(ls(x), rs(x)), swap(lef(x), rig(x)), f[x].rev ^= 1; } void PathTag(int x, Tag w) { f[x].val = f[x].val + w; f[x].pat = f[x].pat + w; f[x].tpa = f[x].tpa + w; } void SubTag(int x, Tag w) { f[x].sub = f[x].sub + w; f[x].tsu = f[x].tsu + w; } void Down(int x, int t) { if (!t) { if (f[x].rev) Rev(ls(x)), Rev(rs(x)), f[x].rev = false; if (f[x].tpa.NE()) PathTag(ls(x), f[x].tpa), PathTag(rs(x), f[x].tpa), f[x].tpa = Tag(); if (f[x].tsu.NE()) SubTag(ls(x), f[x].tsu), SubTag(rs(x), f[x].tsu), SubTag(ms(x), f[x].tsu), f[x].tsu = Tag(); } else { if (f[x].tsu.NE()) { SubTag(ls(x), f[x].tsu), SubTag(rs(x), f[x].tsu); SubTag(ms(x), f[x].tsu), PathTag(ms(x), f[x].tsu); f[x].tsu = Tag(); } } } void Pushdown(int x, int t) { if (Nrt(x)) Pushdown(fa(x), t); Down(x, t); } void Pushup(int x, int t) { lef(x) = ls(x) ? lef(ls(x)) : x; rig(x) = rs(x) ? rig(rs(x)) : x; if (!t) { f[x].pat = f[ls(x)].pat + Dat(1, f[x].val, f[x].val, f[x].val) + f[rs(x)].pat; f[x].sub = f[ls(x)].sub + f[ms(x)].sub + f[rs(x)].sub; } else { f[x].sub = f[ls(x)].sub + f[rs(x)].sub + f[ms(x)].sub + f[ms(x)].pat; } } void Rot(int x, int t) { int y = fa(x), z = fa(y), d = Get(x), p = f[x].ch[!d]; if (z) f[z].ch[Get(y)] = x; if (p) fa(p) = y; fa(x) = z, f[x].ch[!d] = y; fa(y) = x, f[y].ch[d] = p; Pushup(y, t), Pushup(x, t); } void Splay(int x, int t, int tar = 0) { for (Pushdown(x, t); Nrt(x) && fa(x) != tar; Rot(x, t)) if (Nrt(fa(x)) && fa(fa(x)) != tar) Rot(Get(x) == Get(fa(x)) ? fa(x) : x, t); } void Del(int x) { // R if (ls(x)) { int y = rig(ls(x)); Splay(y, 1, x), Set(rs(x), y, 1), Set(y, fa(x), 2), Pushup(y, 1), Pushup(fa(x), 0), Clear(x); } else Set(rs(x), fa(x), 2), Pushup(fa(x), 0), Clear(x); } void Splice(int x) { // R Splay(x, 1); int y = fa(x); Splay(y, 0), Down(x, 1); if (rs(y)) swap(fa(ms(x)), fa(rs(y))), swap(ms(x), rs(y)), Pushup(x, 1), Pushup(y, 0); else Set(ms(x), y, 1), Del(x), Pushup(y, 0); } void Access(int x) { // C Splay(x, 0); if (rs(x)) { int y = NewNode(); Set(ms(x), y, 0), Set(rs(x), y, 2), Set(y, x, 2), Pushup(y, 1), Pushup(x, 0); } for (int y = x; fa(y); y = fa(y)) Splice(fa(y)); Splay(x, 0); } int rt; void Makert(int x) { Access(x), Rev(x); } int Find(int x) { return Access(x), lef(x); } void Split(int x, int y) { Makert(x), Access(y); } void MPath(int x, int y, Tag w) { Split(x, y), PathTag(y, w); } void MSub(int x, Tag w) { Split(rt, x), f[x].val = f[x].val + w, SubTag(ms(x), w), Pushup(x, 0); } Dat QPath(int x, int y) { return Split(x, y), f[y].pat; } Dat QSub(int x) { return Split(rt, x), f[ms(x)].sub + Dat(1, f[x].val, f[x].val, f[x].val); } void Link(int x, int y) { Access(x), Makert(y), Set(y, x, 1), Pushup(x, 0); } void Chgfa(int x, int y) { if (x == rt || x == y) return; Split(rt, x); int p = rig(ls(x)); ls(x) = fa(ls(x)) = 0, Pushup(x, 0); if (Find(x) == Find(y)) Link(x, p); else Link(x, y); } int n, m; int eu[100005], ev[100005]; int main() { scanf("%d%d", &n, &m), cnt = n; for (int i = 1; i < n; ++i) scanf("%d%d", eu + i, ev + i); for (int i = 1; i <= n; ++i) scanf("%d", &f[i].val), Pushup(i, 0); for (int i = 1; i < n; ++i) Link(eu[i], ev[i]); scanf("%d", &rt); while (m--) { int op, x, y, z; scanf("%d", &op); if (op == 0 || op == 5) { scanf("%d%d", &x, &y); MSub(x, {op != 0, y}); } else if (op == 1) { scanf("%d", &rt); } else if (op == 2 || op == 6) { scanf("%d%d%d", &x, &y, &z); MPath(x, y, {op != 2, z}); } else if (op == 3 || op == 4 || op == 11) { scanf("%d", &x); Dat res = QSub(x); if (op == 3) printf("%d\n", res.min); else if (op == 4) printf("%d\n", res.max); else printf("%d\n", res.sum); } else if (op == 7 || op == 8 || op == 10) { scanf("%d%d", &x, &y); Dat res = QPath(x, y); if (op == 7) printf("%d\n", res.min); else if (op == 8) printf("%d\n", res.max); else printf("%d\n", res.sum); } else if (op == 9) { scanf("%d%d", &x, &y); Chgfa(x, y); } } return 0; }
简单萌萌哒 Top Tree(下)。 还没写完,可以去看参考链接。
参考链接:
- Top Tree 相关理论扯淡 - ExplodingKonjac
- 静态 Top Tree 画图
- 浅谈 Top Tree - jerry3128
- Top tree 相关东西的理论、用法和实现 - 论文哥
- Sone1,从 LCT 到 SATT 的跃进 - EnofTaiPeople
- SATT 学习笔记 - F7487(就是 wiki 那篇)
- Top Tree 树上邻域数点 - EnofTaiPeople
- 静态 Top Tree 入门 - chifan-duck
- 静态 Top Tree 学习笔记 - alphagem
- 这个世界就是一棵巨大的 SATT - 251Sec
- Top Cluster, Top Tree - nelofus
- 动态换根 DP - jerry3128
- 原论文 - Tarjan, Werneck
拓展阅读:
本文作者:Laijinyi
本文链接:https://www.cnblogs.com/laijinyi/p/18373391/Top-Tree-1
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步