动态树笔记
不知道“树链剖分”、“全局平衡二叉树”等应不应该归类到“动态树”里面...
解决动态树问题的本质是将原树映射到一个高度为 的树上。
树链剖分
主要是重链剖分,具体略. 支持:
- 链修改
- 链查询
- 子树修改
- 子树查询
这里的修改、查询需要满足可以用数据结构维护.
一般两只 log.
LCT
全称 Link-Cut-Tree,拥有以下函数:
- , , , , ,
- , , ,
具体略.
支持:
- 链修改
- 链查询
- 连边、断边
- 判断连通
- 子树查询可减信息
一只 log
全局平衡二叉树
重链剖分,每条链像 LCT 一样维护成一棵二叉树,如此建树:
记每个点的权值为轻子树大小之和 + 1,求出链的加权中点作为根,然后递归建树.(加权中点:左边之和与右边之和的差最小)
跳轻边,最多 次;跳树边,轻儿子 size 翻倍,故总树高 .
链修改、链查询可拆为二叉树上子树修改、子树查询
子树修改、子树查询等可维护轻儿子的信息、标记
支持:
- 链修改
- 链查询
- 子树修改
- 子树查询
可爱的单 log 噢
ETT
全称 Euler Tour Tree,通过维护欧拉遍历序来维护树
欧拉遍历序(ETR):维护一个序列,DFS 时每访问到一个点或一条有向边就加入序列. 这样序列长度为 .
因为是维护序列,所以用任意平衡树都可以
加入点的目的是存储点上的信息,这在 ETR 上可以理解为加入自环
这个序列本身就是一个环
- 换根
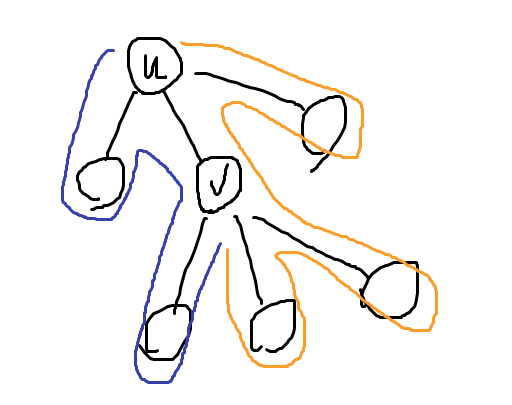
找到自环 的位置,断开成两段,序列顺序由“蓝、黄”变成“黄、蓝”。
- 加边
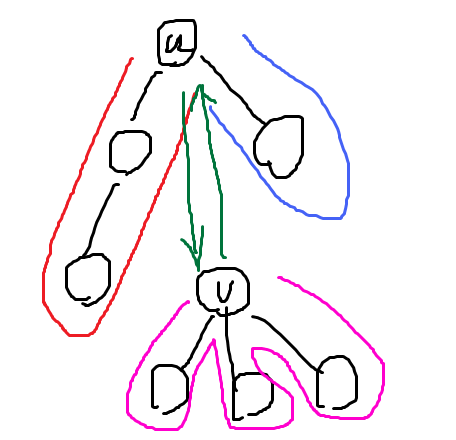
让 变成根,然后让 作为 的儿子即可.
找到自环 的位置,在后面插入绿 + 粉。
- 删边
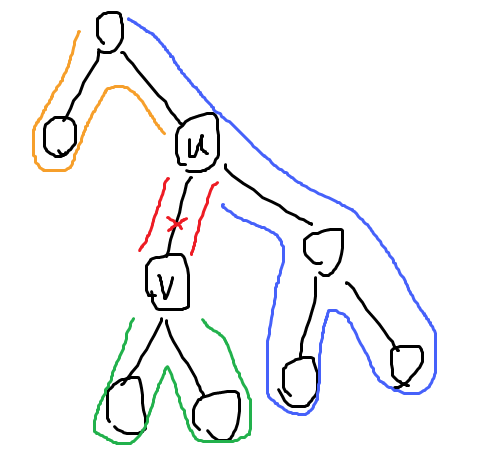
找到边 的位置,断成三段,蓝、黄合并
- 路径和查询
需要信息具有可减性,这样你遍历完一个子树过后信息就变成 0 了,抵消掉了
设边权全为 1,假如询问 的路径长度,把向下走的边看成 (,把向上走的边看成 )
取出 到 这一段的括号序列长度就是答案
信息的合并:括号序列一定形如 )))(((( 这样
两个括号序列合并,先拼接起来,再消去匹配的括号
若边权非 1,可以用同样的逻辑去做
- 连通块修改 + 查询
显然转化为区间修改、区间查询
注意到 ETT 不好快速找到父亲和自己代表的子树,多用于维护无根树,支持:
- 换根
- 加边
- 删边
- 连通块的修改 / 查询
- 询问路径长度
“换根”操作与“子树的修改 / 查询”是矛盾的,因为换根使得儿子的顺序混乱了
以下内容不保熟
如何改进?一种思路是维护 ETT 的同时维护一棵 LCT,LCT 只维护树的形态
可以维护一个性质:LCT 中 的实儿子作为 ETT 中的第一个儿子
考虑链修改:假如修改 ,先令 这一段在 LCT 上是一段实链
然后发现 这一段在 ETT 中是一段连续的区间!就可以修改了.
考虑换根:假如根由
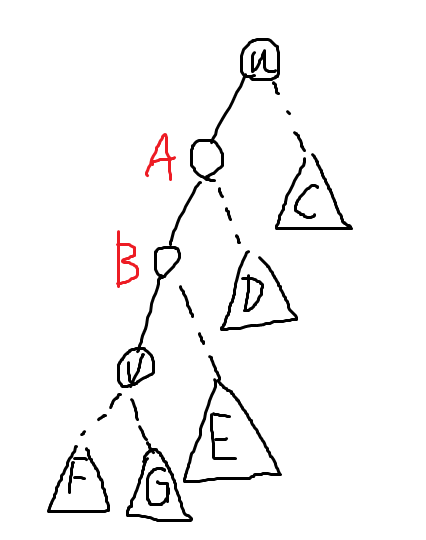
可以先 access(v),然后找到 的位置,考虑入栈序、出栈序
- 换之前:
- 换之后:
找到 的位置 ,前后分别在 LCT 上打翻转标记即可,标记的应用写起来比较复杂
不保熟内容结束
但是谁写呢 ╮(╯▽╰)╭
UPD:还真有人写
加上不保熟内容,他就可以做 Sone 1 了,但是双 log 常数大还难写 QAQ
AAAT
这部分参考了这篇博客
其实就是魔改版 LCT,思路比较简单
注意到在 LCT 里面我们想要维护虚子树所有信息
那么考虑直接用平衡树维护一个点所有虚儿子
因为虚儿子之间并无先后顺序可言,且为了保证复杂度能均摊,我们采用 Leafy Splay 维护,易知点数仍然
如图(懒得画图了,采用神 Claris 的图片):
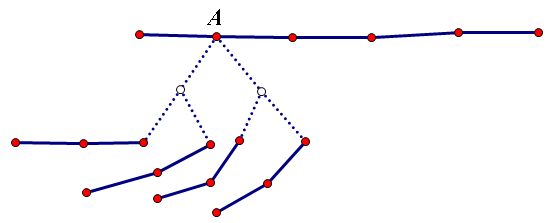
对于下面这棵以 1 为根的树
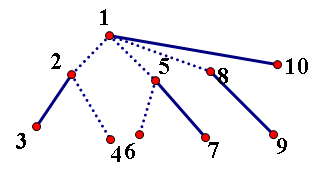
在 AAA 树中是这样维护的
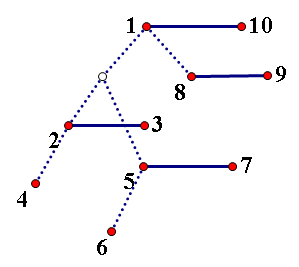
考虑一些基本函数与实现
每个点有 son[0],son[1] 表示实链 Splay 的两个儿子,son[2],son[3] 表示虚边 Splay 的两个儿子
- 操作:在 的虚子树内新增点 ,必要的话新增内部白点.
- 操作:把 与他父亲之间的虚边断开,必要的话删除没用的内部白点.
- 操作:把 到根路径上的所有边变成实边,并把 向他所有儿子的边变成虚边.
考虑普通 LCT 的 Access 过程:
void access(int x) { for (int y = 0; x; y = x, x = fa[x]) { splay(x); son[x][1] = y; up(x); } }
每一步都是实虚边的转化,有了 和 操作,可以很自然的改写成:
void access(int x) { for (int y = 0; x; y = x, x = fa[x]) { splay(x); del(y); add(x, son[x][1]); setson(x, 1, y); up(x); } }
- 操作:与 LCT 一致,注意只交换
son[0]和son[1]. - 操作:
考虑普通 LCT 的 Link 过程:
void link(int x, int y) { makeroot(x); splay(x); f[x] = y; }
可以很自然的改写成:
void link(int x, int y) { makeroot(x); splay(x); add(y, x); }
- 操作:与 LCT 一致.
- 操作:与 LCT 一致.
- 子树操作:
方便起见首先 ,这样 向它的孩子连着的肯定都是虚边, 的子树部分就是 的虚边 Splay。
void changetree(int x, tag p) { access(x); splay(x); val[x] = atag(val[x], p); for (int i = 2; i < 4; i++) if(son[x][i]) tagtree(son[x][i], p, 1); up(x); splay(x); } data asktree(int x) { access(x); splay(x); data t = data(val[x]); for (int i = 2; i < 4; i++) if (son[x][i]) t = t + asum[son[x][i]]; return t; }
做完了,可以证明是单 log 的。
他可以做 Sone 1,讲一下维护方式:
一个点总共维护的信息有:
- :这个点是否为内部白点
- :这个点的点权
- :链上信息和
- :子树信息和(不包括链上)
- :所有信息和
csum[x] = val[x] + csum[son[x][0]] + csum[son[x][1]]; tsum[x] = tsum[son[x][0]] + tsum[son[x][1]] + asum[son[x][2]] + asum[son[x][3]]; asum[x] = csum[x] + tsum[x]
维护的标记有:
- :翻转标记
- :链修改标记
- :子树修改标记(不包括链上)
的下传方法:
- 如果是在实链中的下传,直接下传到 ,无需修改。
- 如果是虚边 Splay 中下传到内部点,下传到 并修改。
- 如果是虚边 Splay 中下传到外部点,下传到 和 并修改。
同时还需要做内存回收。然后做完了。
SATT
压轴内容,喜闻乐见
很可惜的是,他被安排到了我的另一篇文章
~~ 完结撒花 ~~
本文作者:Laijinyi
本文链接:https://www.cnblogs.com/laijinyi/p/18373384/dynamic-trees
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具