1.上网查找什么是求两个数的最大公约数的欧几里得算法(辗转相除法),提交算法说明和网上链接。
辗转相除法, 又名欧几里德算法(Euclidean algorithm),是求最大公约数的一种方法。它的具体做法是:
用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
step1: 将两数中大的那个数放在m中,小的放在n中。
step2: 求出m被n除后的余数r。
step3: 若余数为0则执行步骤(7),否则执行步骤(4)。
step4: 把除数作为新的被除数;把余数作为新的除数。
step5: 求出新的余数r。
step6: 重复步骤(3)到(5)。
step7: 输出n,n即为最大公约数。
1 Python代码
m,n = map(int,input("请输入两个数:").split(",")) #输入两个数用逗号分开
if m<n: #如果m比n小,互换m和n的位置
m,n = n,m
r = m%n #求出m除n的余数
while r: #如果余数不为0,进行循环
m=n #把n赋值给m
n=r #把r赋值给n
r = m%n #求余数
print(f"最大公约数是{n}") #输出n,即为最大公约数
1
2
3
4
5
6
7
8
9
10
代码解析:
m,n: 先用split函数把输入用逗号分隔的两个数分离,再用map函数把分离的两个数变成整数,最后分别赋值给m和n。
if: 在后面的代码中m作为被除数,要比n大,所以如果m小于n,则交换m和n的值(Python中不用第三个变量作为中间变量,可直接用上述语句进行变量间值的交换)。
while: 如果余数不为0,则把n赋值给m,r赋值给n,算出新的余数,直到余数变为0,程序结束,得到的n即为最大公约数。
print: 打印出最大公约数。
。
原文链接:https://blog.csdn.net/qq_32532663/article/details/105750361
2. 参考教材,用伪代码(英语或汉语)实现欧几里得算法(辗转相除法),提交伪代码。
Read num1
Read num2
set m to MaX(num1,num2)
Set n to Min(num,num2)
set r to m mod n
if (r = 0)
write n
while r
set n to r
set n to m
set r to m mod n
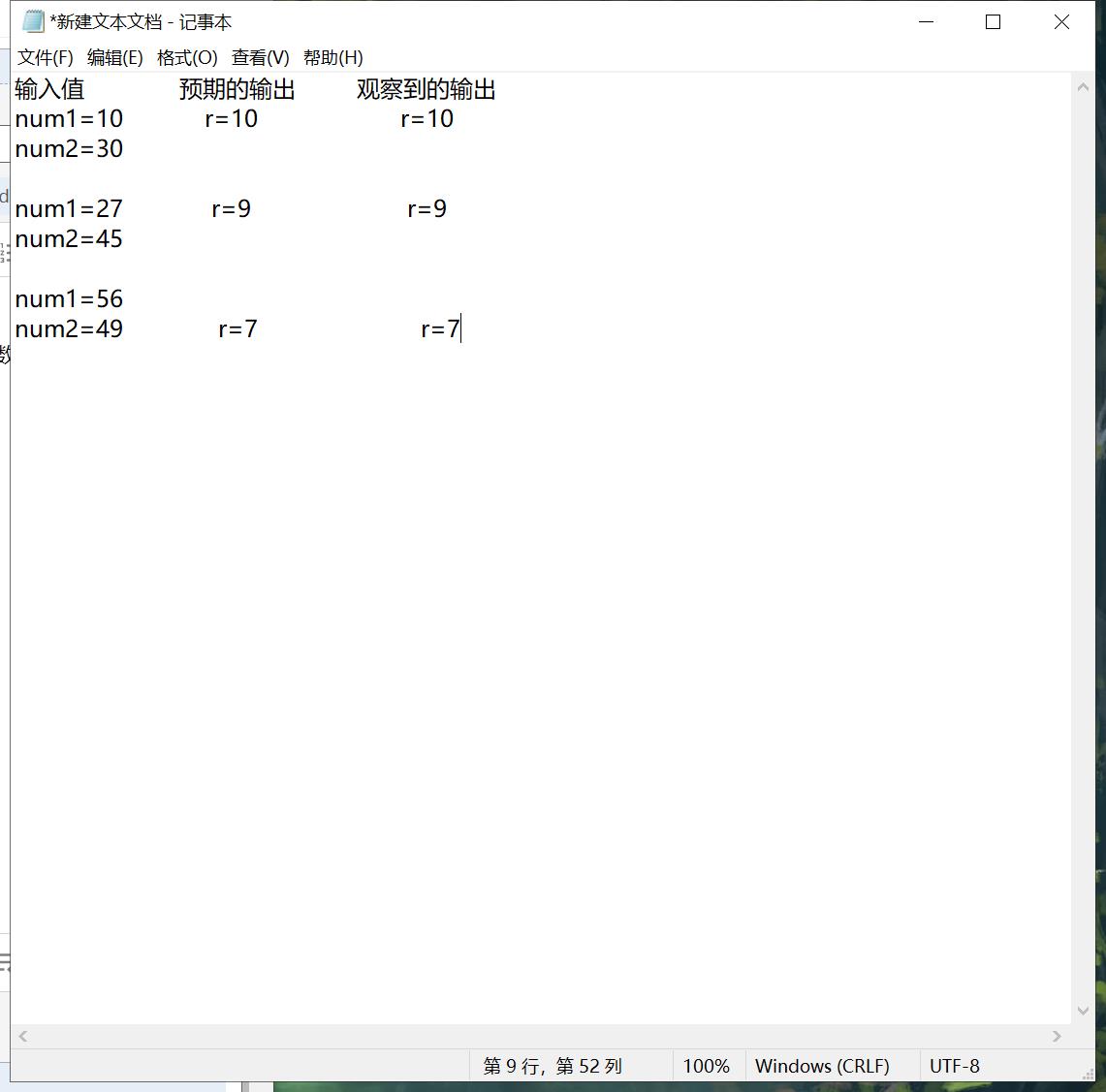
- 选择几组数据,手动走一下伪代码,测试你写的伪代码是否正确,提交测试过程截图。