罗马数字转阿拉伯数字

罗马数字不是位置计数法，这从他的计算方法可以看出
1、相同的数字连写，所表示的数等于这些数字相加得到的数，如：Ⅲ = 3；

2、小的数字在大的数字的右边，所表示的数等于这些数字相加得到的数， 如：Ⅷ = 8；Ⅻ = 12；

3、小的数字，（限于Ⅰ、X 和C）在大的数字的左边，所表示的数等于大数减小数得到的数，如：Ⅳ= 4；Ⅸ= 9；

4、正常使用时，连写的数字重复不得超过三次。（表盘上的四点钟“IIII”例外）

5、在一个数的上面画一条横线，表示这个数扩大1000倍。
缺点：过于复杂 不易传播

class Solution:
def romanToInt(self, s: str) -> int:

    # b = 0
    # for i in s :
    #     if i == 'I':
    #         b += 1
    #     elif i == 'V':
    #         b += 5
    #     elif i == 'X':
    #         b += 10
    #     elif i == 'L':
    #         b += 50
    #     elif i == 'C':
    #         b += 100
    #     elif i == 'D':
    #         b += 500
    #     elif i == 'M':
    #         b += 1000
    # return b

    a = {'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000}
    b = 0
    for i in range(len(s)-1):  #这里遍历字符串的时候选择了遍历每个字符的下标，为了防止下标超出就遍历到len(s)-1
        if a[s[i]] >= a[s[i+1]]:  #如果前大于后则正常相加
            b += a[s[i]]
        else:
            b -= a[s[i]]	#如果前大于后就减去当前值

    b += a[s[len(s)-1]]
    return b

if name == 'main':
s = Solution()
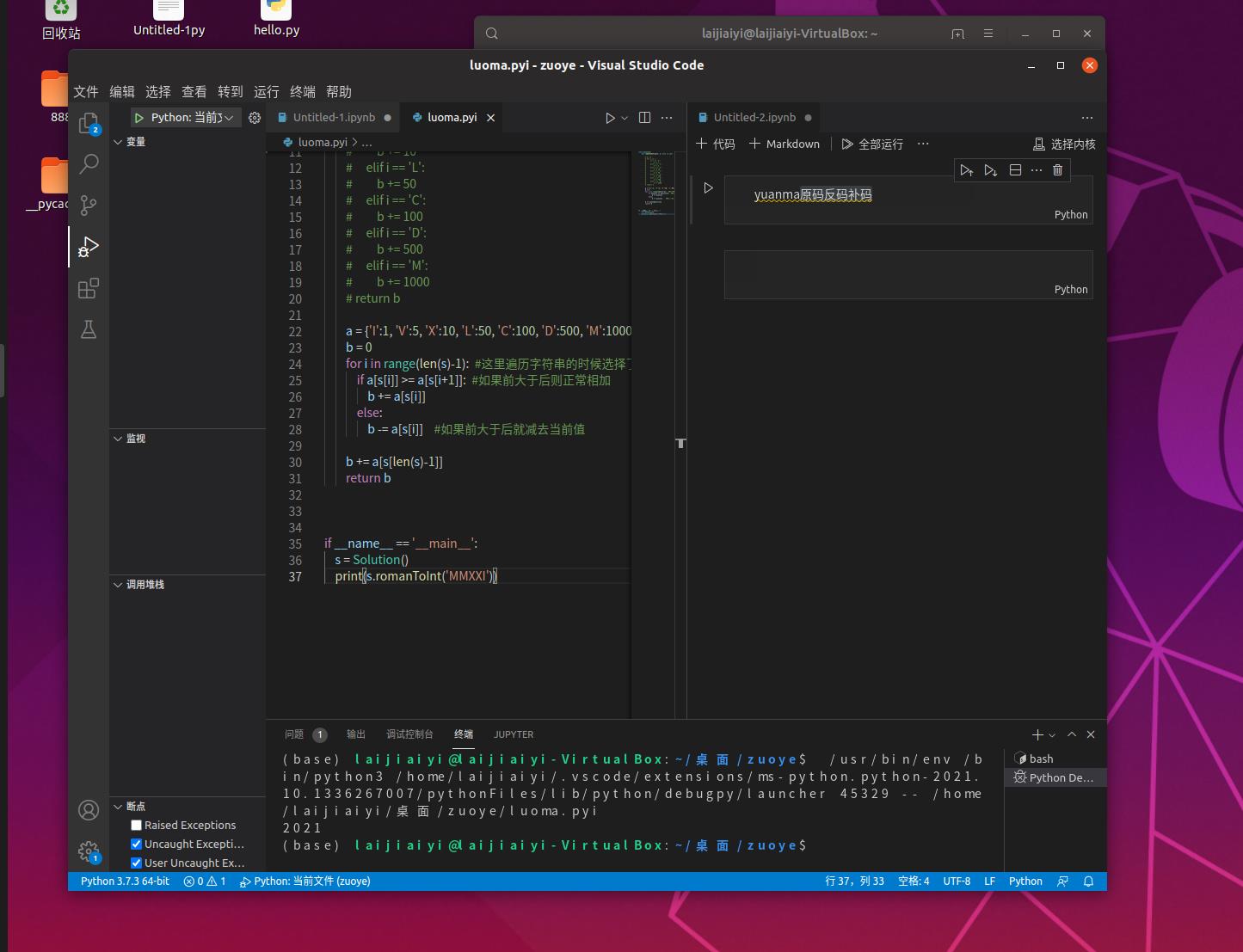
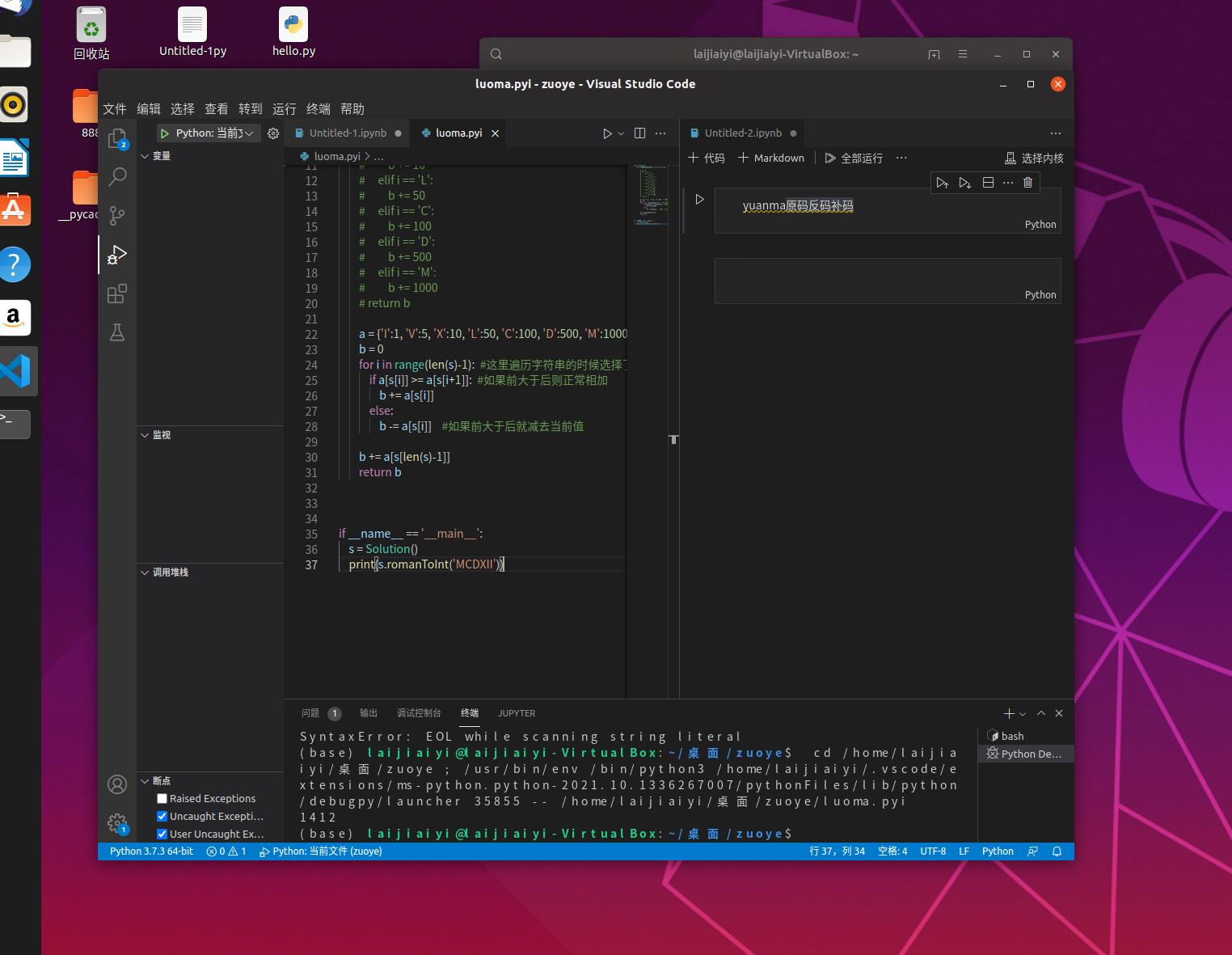
print(s.romanToInt('输入罗马数字'))

将20211412分成两段 2021 1412
分别求得罗马数字为
MMXXI MCDXII