函数与宏定义实验报告
C语言程序设计报告
姓名：赖芳 实验地点：一教524 实验时间：2021.5.27
一、实验目的与要求
1、巩固对函数概念的理解，增强程序设计能力
2、学会调用函数输出三角形，并用for循环的嵌套输出指定的结果
3、掌握C语言中定义函数和通过“值传递”调用函数的方法
4、巩固模块化程序设计的方法
5、掌握递归函数和进一步练习阅读检查与调试修改C程序的方法
二、实验内容
1、实验练习6.5
问题的简单描述
编写程序，从键盘输入两个整数，调用gcd（）函数求它的最大公约数，并输出结果
实验代码
#include<stdio.h>
int gcd(int a,int b)
{
int temp;
int remainder;
if(a<b)
{
temp=a;
a=b;
b=temp;
}
remainder=a%b;
while(remainder!=0)
{
a=b;
b=remainder;
remainder=a%b;
}
return b;
}
main()
{
int x,y;
int fac;
printf("输入两个整数:\n");
scanf("%d,%d",&x,&y);
fac=gcd(x,y);
printf("The great common divisor is%d",fac);
}
运行结果截图
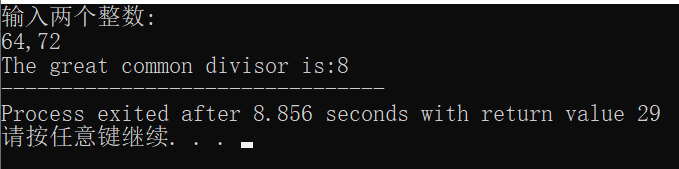
问题分析
辗转相处法不是很懂怎么解决，不知道如何具体去求最大公约数
2、实验练习6.6
问题的简单描述
输入整数n，输出高度为n的等边三角行
实验代码
#include<stdio.h>
void trangle(int n)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n-i;j++)
printf(" ");
for(j=0;j<=2*i;j++)
printf("*");
putchar('\n');
}
}
main()
{
int n;
printf("提示输入一个整数n:");
scanf("%d",&n);
printf("\n");
trangle(n);
}
运行结果截图
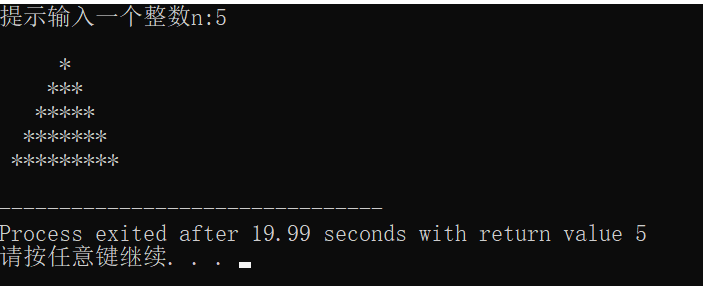
问题分析
首先要计算好空格和*号的个数，有一个约束条件，然后要调用函数
3、实验练习6.7
问题的简单描述
若正整数A的所有因子（包括1但不包括自身，下同）之和为B，而B的因子之和为A，则称A和B为一对亲密数对。求500以内的所有亲密数对
实验代码
#include<stdio.h>
int facsum(int m)
{
int sum=1,f=2;
while(f<=m/2)
{
if(m%f==0)
sum=sum+f;
f=f+1;
}
return sum;
}
main()
{
int m=3,n,k;
while(m<=500)
{
n=facsum(m);
k=facsum(n);
if(m==k&&m<=n)
printf("%d,%d\n",m,n);
m++;
}
}
运行结果截图
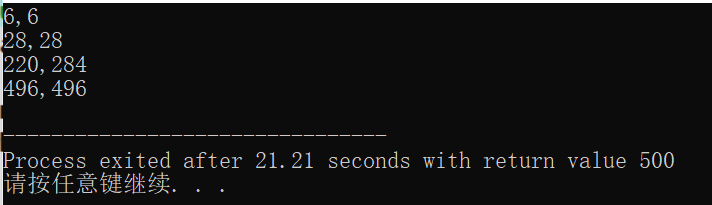
问题分析
用while语句求出m的所有因子，并将它们的和作为返回值，再利用for语句找出亲密数对
4、实验练习6.9
问题的简单描述
根据方法说明，编制计算Ackerman函数的递归函数ack(n,x,y)
实验代码
#include<stdio.h>
int Ack(int n,int x,int y)
{
int a;
if(n==0)
a=x+1;
else if(n==1&&y==0)
a=x;
else if(n==2&&y==0)
a=0;
else if(n==3&&y==0)
a=1;
else if(n>=4&&y==0)
a=2;
else if(n!=0&&y!=0)
a=Ack(n-1,Ack(n,x,y-1),x);
return a;
}
main()
{
int n,x,y,result;
printf("请输入n,x,y:\n");
scanf("%d,%d,%d",&n,&x,&y);
if(n<0||x<0||y<0)
printf("error!");
else
result=Ack(n-1,Ack(n,x,y-1),x);
printf("Ack(%d,%d,%d)=%d\n",n,x,y,result);
}
运行结果截图
问题分析
首先要有多个if……else语句对条件进行判断，这样才能使其顺利进行下去，然后需要调用递归函数。
三、什么是辗转相除法
辗转相除法，又名欧几里德算法（Euclidean algorithm），是求最大公约数的一种方法，它的具体做法是：用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止，如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。（摘自百度文库）
四、实验小结
对于一些函数的运用更加的熟悉，也慢慢的熟悉了函数的递归调用
五、近期个人学习小结
对于C语言这门课程有了一个更加清晰的认知，知道了循环结构和函数等的运用
还是以课本为主，先将重要的知识点过一遍，在看一些不怎么重要的，在看书的过程中结合实际操作一起复习，印象会更加深刻
再把一些比较重要的知识点、习题和例题过一遍
