B. Mashmokh and ACM(dp)
http://codeforces.com/problemset/problem/414/B
Mashmokh's boss, Bimokh, didn't like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh's team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn't able to solve them. That's why he asked you to help him with these tasks. One of these tasks is the following.
A sequence of l integers b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally 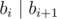 for all i (1 ≤ i ≤ l - 1).
for all i (1 ≤ i ≤ l - 1).
Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007 (109 + 7).
The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).
Output a single integer — the number of good sequences of length k modulo 1000000007 (109 + 7).
3 2
5
6 4
39
2 1
2
In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].
题意:1~n组成的不下降序列,求出序列长度为k的序列种数,每个序列满足序列中的后一个数都能整除前一个数。
思路:后一个数的确定只与前一个数有关,设dp[i][j]表示长度为i的序列中的最后一个数为j,则dp[i][z] = dp[i][z]+dp[i-1][j],其中z是j的倍数。

1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 const int MOD=1000000007; 7 int dp[2002][2002]; 8 int main() 9 { 10 int n,k; 11 while(cin>>n>>k) 12 { 13 memset(dp,0,sizeof(dp)); 14 for (int i = 1; i <= n; i++) 15 dp[1][i] = 1; 16 for (int i = 1; i <= k; i++) 17 { 18 for (int j = 1; j <= n; j++) 19 { 20 for (int z = j; z <= n; z+=j) 21 { 22 dp[i][z] = (dp[i][z]+dp[i-1][j])%MOD; 23 } 24 } 25 } 26 int ans = 0; 27 for (int i = 1; i <= n; i++) 28 { 29 ans+=dp[k][i]; 30 ans%=MOD; 31 } 32 cout<<ans<<endl; 33 } 34 return 0; 35 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号