矩形脉冲在实际应用中十分常见,数字信号可以看做是上下跳变沿构成的很多矩形脉冲串,脉冲雷达也以周期矩形脉冲作为发射信号。
假设周期矩形脉冲信号为\(f(t)\),如下图所示
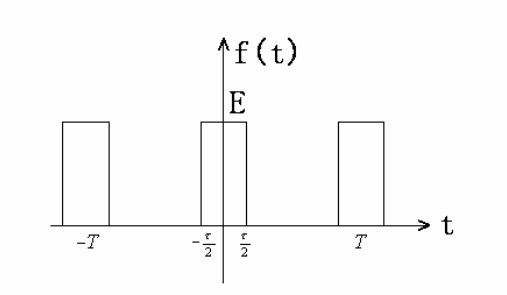
\(f(t)\)的数学表达式可以写成
\[f(t) = \{ \begin{matrix} E& nT-\frac{\tau}{2}<t<nT+\frac{\tau}{2}\\ 0&nT+\frac{\tau}{2}<t<(n+1)T-\frac{\tau}{2} \end{matrix}
\]
这里的\(n\)为整数。
傅里叶级数可以表示为
\[f(t) = \frac{E \tau}{T} \sum^{\infty}_{n=-\infty} \frac{sin{\frac{n \omega_1 \tau}{2}}}{\frac{n \omega_1 \tau}{2}} e^{-jn\omega_1 t}
\]
这里的\(\omega_1 = \frac{1}{T}\)
幅值为0的零点,要求\(sin{\frac{n \omega_1 \tau}{2}} = 0\)。那么,经过一些转化可以得到\(\omega = \frac{2 \pi m}{\tau}\),这里的\(\omega = n \omega_1\),不失一般性。不难看出,这里只有当\(T\)与\(\tau\)满足一定的整数倍关系的时候某些零点才会显现,\(m\)的取指能决定是第几个零点。
一般认为,矩形脉冲的大部分能量在正向第一过零点包括的频带范围内,所以一般认为,矩形脉冲的带宽为
\[Bw = \frac{2 \pi}{\tau}
\]
单个脉冲信号的傅里叶变换。由于周期脉冲信号是无限长的,能量是无限大的,不满足傅里叶变换的条件,所以这里考察单个矩形脉冲的傅里叶变化结果,这里的\(f(t)\)只包括上面截断的一部分
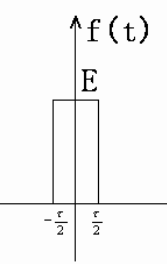
这时候信号丢失了周期信息。
根据傅里叶变换的定义可以很容易的求出结果
\[F(\omega) = E\tau Sa(w\frac{\tau}{2})
\]
过零点信息与上面一样
\[\omega = \frac{2 m \pi}{\tau}
\]





